?🐓?時間復雜度
常用排序的時間復雜度
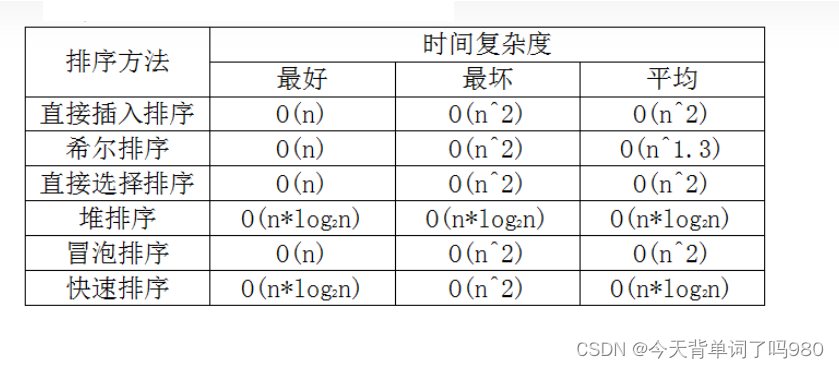
時間頻度
算法需要花費的時間,和它語句執行的次數是成正比的,所以會把一個算法種語句執行次數稱為語句頻度和時間頻度、記作T(n)。
定義
時間復雜度就是找到一個無限接近時間頻度T(n)同數量級的函數,當n趨近于無窮大時,T(n)/f(n)的極限值為不等于零的常數,則稱f(n)是T(n)的同數量級函數。記作T(n)=O(f(n)),稱O(f(n)) 為算法的漸進時間復雜度
通俗一點就是找到一個和T(n)同一量級的函數F(n),寫作O(f(n)),一般在程序中我們會看最內層或者說其執行次數最多的代碼行。
時間復雜度計算
時間復雜度中O是受T(n)種n變化次數最多的那一項影響,比如:T(n) = n^3+n^2+n+23 那這個最大的影響項就是O( n^3)
常見的時間復雜度
階數
| 執行次數函數舉例 | 階 | 非正式術語 |
|---|---|---|
| 12 | O(1) | 常數階 |
| 2n+3 | O(n) | 線性階 |
| n^2+2n+1 | O(n^2) | 平方階 |
| 5log2n+20 | O(logn)/log2n | 對數階 |
| 2n+3nlog2n+19 | O(nlogn) | nlogn階 |
| n^3+n^2+3n+4 | O(n^3) | 立方階 |
| 2^n | O(2^n) | 指數階 |
大小排序
消耗時間從小到大
O(1) < O(logn) < O(n) < O(nlogn) < O(n^2) < O(n^3) < O(2^n) < O(n!) < O(nn)
?🐓?實例
常數階O(1)
沒有任何循環等復雜結構,時間復雜度就是O(1)常量階
代碼示例:
int a = 1; //O(1)
int b = 1; //O(1)
int t = a + b; //該行執行了O(1)次,故O(1)
對數階O(log?n)
在while循環里面,每次都將 i 乘以 2,乘完之后,i 距離 n 就越來越近了。假設循環x次之后,i 就大于 2 了,此時這個循環就退出了,也就是說 2 的 x 次方等于 n,那么 x = log2n也就是說當循環 log2n 次以后,這個代碼就結束了。因此這個代碼的時間復雜度為:O(log2n)?
代碼示例:
int i = 1;
while (i <= n){i = i * 2; //該行執行了O(log2n)次,故O(log2n)
}
線性階O(n)
for循環里面的代碼會執行n遍,因此它消耗的時間是隨著n的變化而變化的,因此這類代碼都可以用O(n)來表示它的時間復雜度。
代碼示例:
for (int i = 1; i <= n; i++) {System.out.println(1); //該行執行了O(n)次,故O(n)
}
線性對數階O(nlog?n)
線性對數階O(nlogN) 其實非常容易理解,將時間復雜度為O(logn)的代碼循環N遍的話,那么它的時間復雜度就是 n * O(logN),也就是了O(nlogN)。
代碼示例:
for (int i = 1; i <= n; i++) { //該循環執行了n次int j = 1;while (j<=n){j = j * 2; //該行執行了O(nlog2n)次,故O(nlog2n)}}
平方階O(n2)
平方階O(n2) 就更容易理解了,就是兩層n的循環嵌套,如果把 O(n) 的代碼再嵌套循環一遍,它的時間復雜度就是 O(n2),這段代碼其實就是嵌套了2層n循環,它的時間復雜度就是 O(nn),即 O(n2) 如果將其中一層循環的n改成m,那它的時間復雜度就變成了 O(mn)。
代碼示例:
for (int i = 1; i <= n; i++) {for (int j = 1; j <= n; j++) {System.out.println(1);//該行執行了O(n2)次,故O(n2)}
}
立方階O(n3)
立方階和平方階差不多,只是多了一層循環,一共有三層n循環,它的時間復雜度就是O(n*n)。
代碼示例:
for (int i = 1; i <= n; i++) {for (int j = 1; j <= n; j++) {for (int k = 1; k <= n; k++) {System.out.println(1);//該行執行了O(n3)次,故O(n3)}}
}
n指數階O(2?)
很少遇見,盡量少,建議少些這種復雜度的代碼。


)












)



