excel統計分析——拉丁方設計

參考資料：生物統計學

? ? ? ? 拉丁方設計也是隨機區組設計，是對隨機區組設計的一種改進。它在行的方向和列的方向都可以看成區組，因此能實現雙向誤差的控制。在一般的試驗設計中，拉丁方常被看作雙區組設計，用于提高發現處理效應差別的效率。

1、設計方法

? ? ? ? 拉丁方是指用字母排成一個階方陣，使得每一行、每一列中每個字母都恰好各出現一次。拉丁方設計（Latin square design）就是利用拉丁方安排試驗的試驗設計，是一種二維設計，用于有三個因素而且每個因素的水平數都相同的研究。如果試驗水平數為k，則共安排k^2個試驗。

2、主要特點

（1）經濟性：通過k的平方個試驗完成三因素各k個水平的試驗，非常節省試驗單位數。如果要從試驗中獲取更多信息時，需要安排“重復拉丁方”試驗，“重復”不是復制相同的拉丁方，而是采用同樣大小而處理排列不同的拉丁方。

（2）勻稱性：均勻性是拉丁方的另一個優點。雖然拉丁方只用一個二維的正方格子表示，但所研究的三個因素各處理在拉丁方中是均勻分布的。

3、試驗結果的統計分析

? ? ? ? 拉丁方設計資料的統計分析采用無重復觀測值的三因素方差分析模型。沒有“重復拉丁方”時，只能分析各因素的主效應。由于各因素水平相同，只考慮主效應，數學模型為：

$x_{ijkl}=\mu+\alpha_i+\beta_j+\gamma _k+\varepsilon _{jikl}$

其中， $x_{ijkl}$ 為A因素i水平B因素j水平C因素k水平的第l個觀測值； $\alpha_i$ 、 $\beta_j$ 、 $\gamma_k$ 為各因素的處理效應； $\varepsilon _{jikl}$ 為誤差。平方和與自由度的分析如下：

$SS_T=\sum x^2-C$ ，? ? ? ? ?? $df_T=a^2-1$

$SS_A=\sum T_i^2/a-C$ ，? ? ? $df_A=a-1$

$SS_B=\sum T_j^2/a-C$ ，? ? ? $df_B=a-1$

$SS_C=\sum T_k^2/a-C$ ，? ? ? $df_B=a-1$

$SS_e=SS_T-SS_A-SS_B-SS_C$ ， $df_e=(a-1)(a-2)$

其中，T為總變異，ABC為各因素的變異，e為誤差；a為因素水平數；Ti為A因素i水平的觀測值之和，Tj為B因素j水平的觀測值之和，Tk為C因素k水平的觀測值之和； $C=T^2/a^2$ ，T為所有觀測值的總和。

4、拉丁方設計的變形

（1）不完全拉丁方設計

? ? ? ? 如果試驗的某一因素與其他因素的水平數不同，這時拉丁方就不再是方陣而是一個矩陣，這時的拉丁方設計為不完全拉丁方設計（incomplete Latin square design）。不完全拉丁方設計資料的統計分析參考平衡不完全區組設計進行平方和分解，試驗處理的平方和需要矯正，重復數、自由度參照公式據實計算。

（2）正交拉丁方設計

? ? ? ? 如果在拉丁方字母（數字）上在疊加一個希臘字母，并且限定每個拉丁字母與希臘字母只相遇一次，此時拉丁方為正交拉丁方。正交拉丁方（crossed Latin square design）即利用正交拉丁方安排試驗的試驗設計。正交拉丁方也是一個二維設計，但客供研究四個因素，但要求每個因素的水平數相同，是拉丁方設計的擴展，并以此可推廣到更多因素的拉丁方設計。

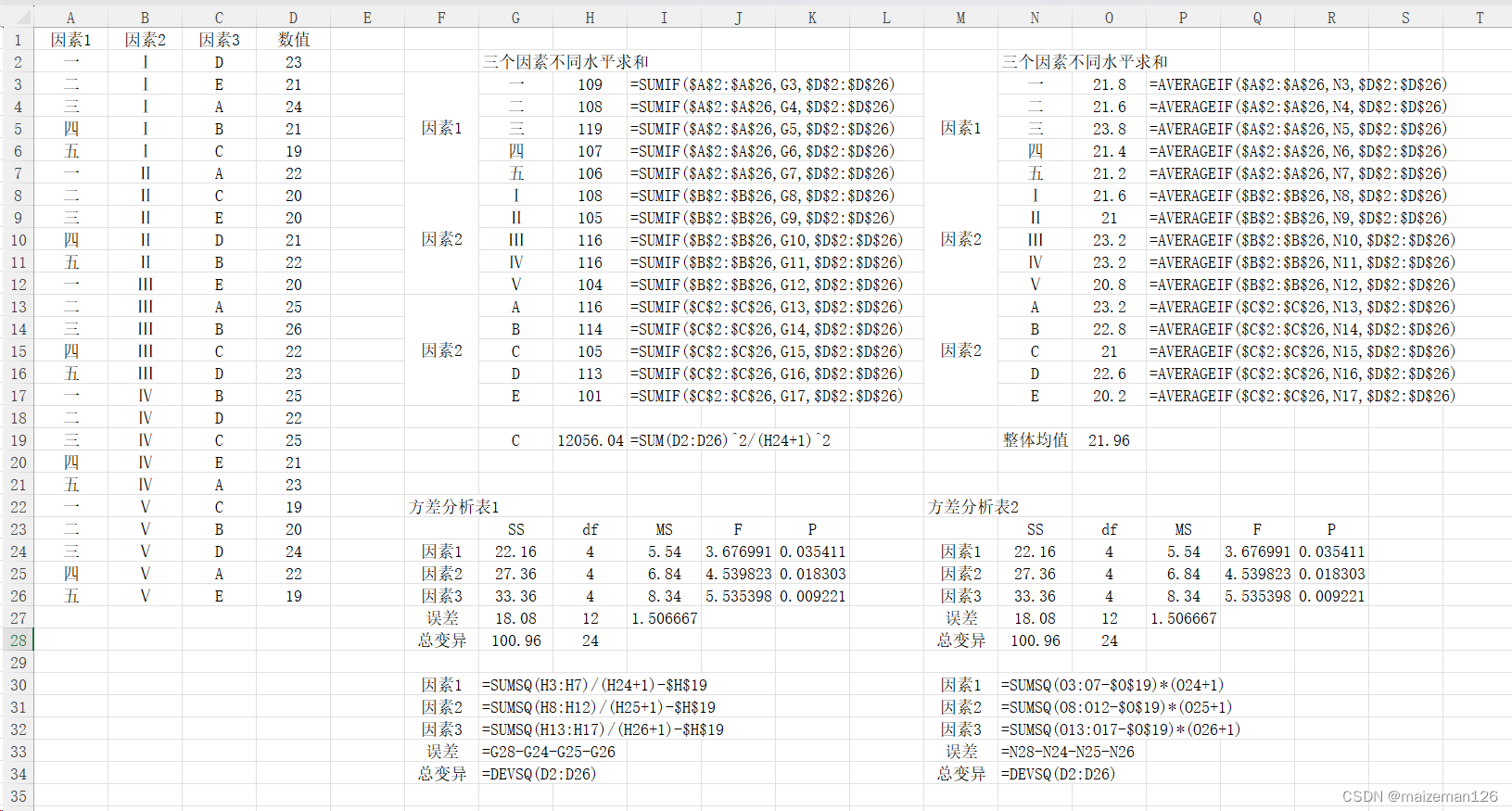
5、案例

因素1的5個水平：用一、二、三、四、五表示

因素2的5個水平：用Ⅰ、Ⅱ、Ⅲ、Ⅳ、Ⅴ表示

因素3的5個水平：用A、B、C、D、E表示

方差分析過程如下：

本文來自互聯網用戶投稿，該文觀點僅代表作者本人，不代表本站立場。本站僅提供信息存儲空間服務，不擁有所有權，不承擔相關法律責任。
如若轉載，請注明出處：http://www.pswp.cn/news/718045.shtml
繁體地址，請注明出處：http://hk.pswp.cn/news/718045.shtml
英文地址，請注明出處：http://en.pswp.cn/news/718045.shtml

如若內容造成侵權/違法違規/事實不符，請聯系多彩編程網進行投訴反饋email:809451989@qq.com，一經查實，立即刪除！