板子合集1.0

原文鏈接：https://blog.csdn.net/JK01WYX/

文章目錄

1.快速冪板子
2.gcd得最大公約數
3.堆優化的dijkstra板子
4.線段樹1板子區間加
- 線段樹的結構關系：
- int作為下標的：
- long long作為下標的：
5.線段樹2板子區間加與乘
6.樹狀數組1板子可修改單個點的前綴和
7.樹狀數組2板子差分數組快速區間加求某個數
8.manacher板子快速求最長回文串的長度
- 原理
- 使用示范，本板子是加#(奇偶長度一起算)的：
- 單獨lamda:
- OI Wiki摘錄的只算單數和雙數的：
9.ST表板子類似歸并的有條理暴力 sparse-table
- ST表部分的代碼：
- 使用示范：
10.LCA倍增板子
- 預處理：
- LCA:
- 主函數外版：
11.KMP板子前綴跳后綴
- 原理：
- 板子：
12.掃描線板子小思路
- 前言：
- 背景：
- 掃描線原理：
- 代碼：
13.龜速乘板子 a*二進制拆分的正數b（mod p）
14.拓展歐幾里得法求逆元
- 板子：
- 使用:
- 原理：
- 拓展歐幾里得算法：
15.二分圖板子匈牙利算法 KM算法
- 原理：
- 板子：
- 使用：
16.盧卡斯定理/Lucas定理板子組合數板子
17.高精度加法，乘法板子
- High precision addition
- High precision multiplication
18.排列組合板子 A C
19.快讀快寫板子
20.分解質因數板子
21.快速選擇數組中的第K個最大元素
22. 26個質數
23.多重背包問題
24.歸并
25.判斷是素數質數
26.素數篩法
- Eratosthenes 篩法（埃拉托斯特尼篩法，簡稱埃氏篩法）篩至平方根
- 分塊篩選
- 線性篩法

1.快速冪板子

快速冪是快速算 a 的 c 次冪

原理：
我們用分治思想是比一個一個乘快的

即比如我們求a的8次方：a1a1 = a2 ,那么我們直接a2a2 = a4，a4*a4 = a8

參數就是幾次冪。返回值是對應參數的冪（這里對p取余了）(一般也把a當參數)

long long a, p;//a^c mod p=s
long long fp(int c)
{if(c==0)return 1;if (c == 1)return a % p;long long tmp = fp(c / 2); if (c % 2 == 0)return tmp * tmp % p;elsereturn tmp * tmp % p * a % p;
}
long long fp(long long a,int c)
{if(c==0)return 1;if (c == 1)return a % MOD;long long tmp = fp(a,c / 2); if (c % 2 == 0)return tmp * tmp % MOD;elsereturn tmp * tmp % MOD * a % MOD;
}

細節解釋：
c == 1就是1次冪。

tmp就是a的c/2次冪。我們要返回c次冪，整數除法是向下取整的。

（比如5次冪，5/2==2，那么需要額外乘一個使得為c次冪）

——————————
非遞歸寫法：(二進制拆分）

#define ll long long
ll mod = 1e9+7;
ll q(ll a,ll b)
{ll s = 1;while(b){if(b&1) s = s * a %mod;a = a * a % mod;b >> 1;}return s;
}

2.gcd得最大公約數

證法一
a可以表示成a = kb + r（a，b，k，r皆為正整數，且r不為0）
假設d是a,b的一個公約數，記作d|a,d|b，即a和b都可以被d整除。
而r = a - kb，兩邊同時除以d，r/d=a/d-kb/d，由等式右邊可知m=r/d為整數，因此d|r
因此d也是b,a mod b的公約數。
因(a,b)和(b,a mod b)的公約數相等，則其最大公約數也相等，得證。
——————

百度百科證法一的一些便于理解的細節：

我們求 a 和 b 的最大公約數。

（如果a是b的倍數，那么b就是最大公約數。）

a>b，a可以表示為 a = kb + r

設d為a和b的最大公約數

對上式等號左右兩端同時除以d，得 a/d = kb/d + r/d

a/d 和 kb/d都是整數，那么r/d也是整數。那么r也是d的倍數。同時r<b，r與b的最大公約數也是d

( r<d是因為r = a%b （由a的表示可知))

那么問題就轉化成求 b 與 r 的最大公約數。

即 gcd(a,b) = gcd(b,a mod b)

r會一直變小，為0時，b就是最大公約數了 （b最小為1，當b為1時，余數必然為0）

——————

（當然再進一次循環就是 a 與 0 。返回a即可）：

long long gcd(long long a,long long b)
{if (a<b)swap(a,b); if (b==0)      return a;elsereturn gcd(b, a % b);
}

3.堆優化的dijkstra板子

1.第一個結構體dis_node把下標和該下標距起點的當前最短路放入一個結構體了，這樣做堆排的時候方便找下標。

2.cmp仿函數是用于堆排比較器的，（試過greater<自己的類型>()是不行的。。）

建的小根堆快速選擇當前最短路（dijkstra的原理）

①tmpdis代表節點之間的距離，有的時候就是1，自己設置吧，dijkstr主函數中算距離用。

②dij代表此點到所有點的最短路，所以我放參數列表當輸出型參數了，許多題可能要用到。

③vector<set>arr代表通路，用set可以去重（有的題可能是多重圖，即含平行邊）。

④加強：自己到自己不用，所以if一下。因為next = cur，會吧dij[cur]給覆蓋掉造成錯誤

    int tmpdis = 1;struct dis_node//放堆里面比長度，但是想知道端點{int dis;int next;bool operator < (const dis_node& a){return dis < a.dis;}dis_node(int d, int n){dis = d; next = n;}};class cmp{public:bool operator()(dis_node a, dis_node b){return a.dis > b.dis;//}};void dijkstr(vector<int>&dij,vector<set<int>>& arr, int ori, int n){priority_queue<dis_node, vector<dis_node>, cmp>heap;vector<int>barr(n + 1);int cur = ori;while (1){//該次點所有可走的for (auto next : arr[cur]){if(next == cur)continue;//next就是下一個點（鄰接表if (dij[next] == 0)dij[next] = dij[cur] + tmpdis;elsedij[next] = min(dij[next], dij[cur] + tmpdis);heap.push(dis_node(dij[next], next));}//該點已使用，已最短，無需再抵達barr[cur] = 1;//最短路中找最短，同時可抵達的while (heap.size()){if (barr[heap.top().next] == 0)break;heap.pop();}if (heap.size() == 0)break;cur = heap.top().next;heap.pop();}}

4.線段樹1板子區間加

類的構造函數寫在類最后了，本板子沒有將左右下標封裝到節點中，而是實時計算的。

建議閱讀：線段樹 - OI Wiki (oi-wiki.org)

線段樹的結構關系：

//		  1
//	  2      3			2^1
//	4   5  6   7		2^2
// 8 9					2^3
//1		log1==0
//2		log2==1		log3==1
//4		log4==2		log5==log6==log7==2
//8
//log5 == 2, +1在第三層，0~3 共四層 4
// 
//完全二叉樹的總結點數就是：
//等比數列求和
//1*（2^  - 1）/(2-1)
//logn + 1層
//pow(2,(int)log2(n)+1)-1
//

int作為下標的：

template<class T>
class ST//segment tree
{struct node{T val;T t;//懶標記//服務后代node(T v = 0) :val(v), t(0){}};int n = a.size();vector<T>a;vector<node>d;
public:void build_tree(int i, int l, int r){if (l == r){d[i].val = a[l];return;}int mid = l + (r - l) / 2;build_tree(i * 2, l, mid);build_tree(i * 2 + 1, mid + 1, r);d[i].val = d[i * 2].val + d[i * 2 + 1].val;}void spread(int i, int l, int r, int aiml, int aimr){int mid = l + (r - l) / 2;if (d[i].t != 0 && l != r){d[i * 2].val += d[i].t * (mid - l + 1);d[i * 2 + 1].val += d[i].t * (r - mid);d[i * 2].t += d[i].t;//可能上上次也沒改d[i * 2 + 1].t += d[i].t;d[i].t = 0;}}T getsum(int l, int r){return _getsum(1, 1, n, l, r);}T _getsum(int i, int l, int r, int aiml, int aimr){if (aiml <= l && r <= aimr)//查詢區間的子集全部加起來return d[i].val;//訪問int mid = l + (r - l) / 2;spread(i, l, r, aiml, aimr);T ret = 0;if (aiml <= mid)ret += _getsum(i * 2, l, mid, aiml, aimr);if (aimr >= mid + 1)ret += _getsum(i * 2 + 1, mid + 1, r, aiml, aimr);return ret;}void update(int l, int r, ll val){_update(1, 1, n, l, r, val);//加并掛標記}void _update(int i, int l, int r, int aiml, int aimr, ll val){if (aiml <= l && r <= aimr){d[i].val += val * (r - l + 1);d[i].t += val;return;}int mid = l + (r - l) / 2;spread(i, l, r, aiml, aimr);if (aiml <= mid)_update(i * 2, l, mid, aiml, aimr, val);if (aimr >= mid + 1)_update(i * 2 + 1, mid + 1, r, aiml, aimr, val);//我們只對葉子更新了，（別多想懶標記）d[i].val = d[i * 2].val + d[i * 2 + 1].val;}ST(vector<T>arr){a = arr;n = a.size() - 1;d = vector<node>(pow(2, (int)log2(n) + 1 + 1) - 1 + 1);build_tree(1, 1, n);}
};

long long作為下標的：

#define ll long long
template<class T>
class ST//segment tree
{struct node{T val;T t;//懶標記//服務后代node(T v = 0) :val(v), t(0){}};ll n = a.size();vector<T>a;vector<node>d;
public:void build_tree(ll i, ll l, ll r){if (l == r){d[i].val = a[l];return;}ll mid = l + (r - l) / 2;build_tree(i * 2, l, mid);build_tree(i * 2 + 1, mid + 1, r);d[i].val = d[i * 2].val + d[i * 2 + 1].val;}void spread(ll i, ll l, ll r, ll aiml, ll aimr){ll mid = l + (r - l) / 2;if (d[i].t != 0 && l != r){d[i * 2].val += d[i].t * (mid - l + 1);d[i * 2 + 1].val += d[i].t * (r - mid);d[i * 2].t += d[i].t;//可能上上次也沒改d[i * 2 + 1].t += d[i].t;d[i].t = 0;}}T getsum(ll l, ll r){return _getsum(1, 1, n, l, r);}T _getsum(ll i, ll l, ll r, ll aiml, ll aimr){if (aiml <= l && r <= aimr)//查詢區間的子集全部加起來return d[i].val;//訪問ll mid = l + (r - l) / 2;spread(i, l, r, aiml, aimr);T ret = 0;if (aiml <= mid)ret += _getsum(i * 2, l, mid, aiml, aimr);if (aimr >= mid + 1)ret += _getsum(i * 2 + 1, mid + 1, r, aiml, aimr);return ret;}void update(ll l, ll r, ll val){_update(1, 1, n, l, r, val);//加并掛標記}void _update(ll i, ll l, ll r, ll aiml, ll aimr, ll val){if (aiml <= l && r <= aimr){d[i].val += val * (r - l + 1);d[i].t += val;return;}ll mid = l + (r - l) / 2;spread(i, l, r, aiml, aimr);if (aiml <= mid)_update(i * 2, l, mid, aiml, aimr, val);if (aimr >= mid + 1)_update(i * 2 + 1, mid + 1, r, aiml, aimr, val);//我們只對葉子更新了，（別多想懶標記）d[i].val = d[i * 2].val + d[i * 2 + 1].val;}ST(vector<T>arr){a = arr;n = a.size() - 1;d = vector<node>(pow(2, (ll)log2(n) + 1 + 1) - 1 + 1);build_tree(1, 1, n);}
};

5.線段樹2板子區間加與乘

當對區間即有加操作，又有乘操作時：

//乘法滿足分配率！！，所以乘懶標記可以“攻擊”加懶標記
//策略：兩個標記都安排
//當乘標記來臨時，對自己和懶標記都乘//假設都沒有向后延伸
//
//（特別好的分析：）
//當加標記來臨時，正常加就好啦，因為乘已經對加處理啦
//
//兩個一起來臨呢，先乘！！！！！！！！！！！！！！！！！
//(乘已經對這部分加處理過了)

template<class T>
class ST//segment tree
{struct node{T val;T t1;T t2;//乘node(T v = 0) :val(v), t1(0), t2(1)//x2x3 == x6{}};ll n = a.size();vector<T>a;vector<node>d;
public:void build_tree(ll i, ll l, ll r){if (l == r){d[i].val = a[l] % MOD;return;}ll mid = l + (r - l) / 2;build_tree(i * 2, l, mid);build_tree(i * 2 + 1, mid + 1, r);d[i].val = d[i * 2].val + d[i * 2 + 1].val;}void spread(ll i, ll l, ll r, ll aiml, ll aimr){//懶惰ll mid = l + (r - l) / 2;//if ((d[i].t1 != 0 || d[i].t2 != 1) && l != r)//{T t1 = d[i].t1, t2 = d[i].t2;//先乘d[i * 2].val = (d[i * 2].val * t2) % MOD;d[i * 2].t1 = (d[i * 2].t1 * t2) % MOD;d[i * 2].t2 = (d[i * 2].t2 * t2) % MOD;d[i * 2 + 1].val = (d[i * 2 + 1].val * t2) % MOD;d[i * 2 + 1].t1 = (d[i * 2 + 1].t1 * t2) % MOD;d[i * 2 + 1].t2 = (d[i * 2 + 1].t2 * t2) % MOD;//后加d[i * 2].val = (d[i * 2].val + t1 * (mid - l + 1)) % MOD;d[i * 2 + 1].val = (d[i * 2 + 1].val + t1 * (r - mid)) % MOD;d[i * 2].t1 = (d[i * 2].t1 + t1) % MOD;d[i * 2 + 1].t1 = (d[i * 2 + 1].t1 + t1) % MOD;//復原d[i].t1 = 0;d[i].t2 = 1;//}/// }ll getsum(ll l, ll r){return _getsum(1, 1, n, l, r);}ll _getsum(ll i, ll l, ll r, ll aiml, ll aimr){if (aiml <= l && r <= aimr)return d[i].val;ll mid = l + (r - l) / 2;spread(i, l, r, aiml, aimr);ll ret = 0;if (aiml <= mid)ret = (ret + _getsum(i * 2, l, mid, aiml, aimr)) % MOD;if (aimr >= mid + 1)ret = (ret + _getsum(i * 2 + 1, mid + 1, r, aiml, aimr)) % MOD;return ret;}void update1(ll l, ll r, ll val){_update1(1, 1, n, l, r, val);//加并掛標記}void _update1(ll i, ll l, ll r, ll aiml, ll aimr, T val){if (aiml <= l && r <= aimr){d[i].t1 = (d[i].t1 + val) % MOD;d[i].val = (d[i].val + val * (r - l + 1)) % MOD;return;}ll mid = l + (r - l) / 2;spread(i, l, r, aiml, aimr);if (aiml <= mid)_update1(i * 2, l, mid, aiml, aimr, val);if (aimr >= mid + 1)_update1(i * 2 + 1, mid + 1, r, aiml, aimr, val);d[i].val = (d[i * 2].val + d[i * 2 + 1].val) % MOD;}void update2(ll l, ll r, T val){_update2(1, 1, n, l, r, val);//加并掛標記}void _update2(ll i, ll l, ll r, ll aiml, ll aimr,T val){if (aiml <= l && r <= aimr){d[i].val = (d[i].val * val) % MOD;d[i].t1 = (d[i].t1 * val) % MOD;d[i].t2 = (d[i].t2 * val) % MOD;return;}ll mid = l + (r - l) / 2;spread(i, l, r, aiml, aimr);if (aiml <= mid)_update2(i * 2, l, mid, aiml, aimr, val);if (aimr >= mid + 1)_update2(i * 2 + 1, mid + 1, r, aiml, aimr, val);d[i].val = (d[i * 2].val + d[i * 2 + 1].val) % MOD;}ST(vector<T>arr){a = arr;n = a.size() - 1;d = vector<node>(pow(2, (ll)log2(n) + 1 + 1) - 1 + 1);build_tree(1, 1, n);}
};

6.樹狀數組1板子可修改單個點的前綴和

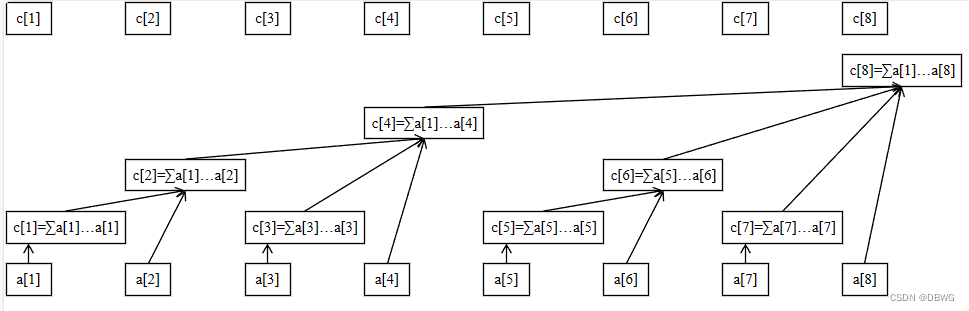
請添加圖片描述

樹狀數組中，規定 c[x] 管轄的區間長度為 $2^{k}$ ，其中：

設二進制最低位為第 0 位，則 k 恰好為 x 二進制表示中，最低位的 1 所在的二進制位數；
2^k（c[x] 的管轄區間長度）恰好為 x 二進制表示中，最低位的 1 以及后面所有 0 組成的數。

對于lowbit的證明，注意正數的原碼反碼和補碼是相同的。

add函數給該節點增加值后，while循環一直找父節點加值。

template<class T>
class BIT//Binary Indexed Tree
{
public:ll n;//a的大小vector<T>a;//原數組vector<T>c;//樹狀數組ll lowbit(ll a){return a & -a;}T getsum(ll i){T sum = 0;while (i > 0){sum += c[i];i -= lowbit(i);}return sum;}void add(ll i, T v){while (i <= n){c[i] += v;i = i + lowbit(i);}}BIT(vector<T>_a){a = _a;n = a.size() - 1;c = vector<T>(n + 1);//直接把樹建好for (ll i = 1; i <= n; i++){add(i, a[i]);}}
};

7.樹狀數組2板子差分數組快速區間加求某個數

add可以給一個數加值

如果想給一段區間加值，有沒有更快的操作：add1

實際上，這個是差分數組，差分的前綴和就是這個位置的數值，所以是用來求單個數的

template<class T>
class BIT//Binary Indexed Tree
{
public:ll n;//a的大小vector<T>a;//原數組vector<T>c;//樹狀數組//還是求和，只不過傳過來的是差分了ll lowbit(ll a){return a & -a;}T getsum(ll i){T sum = 0;while (i > 0){sum += c[i];i -= lowbit(i);}return sum;}void add(ll i, ll v){while (i <= n){c[i] += v;i += lowbit(i);}}void add1(ll l, ll r, ll v){add(l, v);add(r + 1, -v);}BIT(vector<T>_a){a = _a;n = a.size() - 1;c = vector<T>(n + 1);//直接把樹建好for (ll i = 1; i <= n; i++){add(i, a[i]);}}
};

使用示范：

//差分構造：
void solve()
{int n, m;cin >> n >> m;vector<int>arr(n + 1);for (int i = 1; i <= n; i++){cin >> arr[i];}vector<int>d(n + 1);d[1] = arr[1];for (int i = 2; i <= n; i++){d[i] = arr[i] - arr[i - 1];}BIT<int> demo(d);/// <summary>for (int i = 1; i <= m; i++){int op;cin >> op;if (op == 1){int x, y, k;cin >> x >> y >> k;demo.add1(x, y, k);}else if (op == 2){int x;cin >> x;cout << demo.getsum(x) << endl;}}
}

8.manacher板子快速求最長回文串的長度

原理

r記錄當前最右的回文（l（左）與之對應），這樣我們后來在r中偏右進行判斷時，因為l r之間是回文，所以可以參照中偏左對應的位置，少判斷許多次。

使用示范，本板子是加#(奇偶長度一起算)的：

d[i]表示以位置i為中心的最長回文串的半徑長度

d數組的值-1即是本位置最長回文長度，原因看最下面注釋。

void solve()
{string str, aim;cin >> str;aim += "#";for (int i = 0; i < str.size(); i++){aim += str[i];aim += "#";}vector<int>d(aim.size());//  abcbaauto manacher = [&](string s) {int l = 0, r = -1;for (int i = 0; i < s.size(); i++){int k = i > r ? 1 : min(d[l + r - i], r - i + 1);//左邊對稱相同，但不越界//k是半徑，加了等于下一位//樸素算法while (i - k >= 0 && i + k <= s.size() && s[i - k] == s[i + k])k++;d[i] = k;if (i + d[i] - 1 > r){r = i + d[i] - 1;l = i - d[i] + 1;}}};manacher(aim);int ans = 0;for (auto x : d){ans = max(ans, x);}//d[i]表示i（不包括i）左右的對稱的長度// # a # b # a #//		 - - - -// # a # b # b # a #//		   - - - - -cout << ans - 1;
}

單獨lamda:

//  abcbaauto manacher = [&](string s) {int l = 0, r = -1;for (int i = 0; i < s.size(); i++){int k = i > r ? 1 : min(d[l + r - i], r - i + 1);//左邊對稱相同，但不越界//k是半徑，加了等于下一位//樸素算法while (i - k >= 0 && i + k <= s.size() && s[i - k] == s[i + k])k++;d[i] = k;if (i + d[i] - 1 > r){r = i + d[i] - 1;l = i - d[i] + 1;}}};

————

OI Wiki摘錄的只算單數和雙數的：

vector<int> d1(n);
for (int i = 0, l = 0, r = -1; i < n; i++) {int k = (i > r) ? 1 : min(d1[l + r - i], r - i + 1);while (0 <= i - k && i + k < n && s[i - k] == s[i + k]) {k++;}d1[i] = k--;if (i + k > r) {l = i - k;r = i + k;}
}

vector<int> d2(n);
for (int i = 0, l = 0, r = -1; i < n; i++) {int k = (i > r) ? 0 : min(d2[l + r - i + 1], r - i + 1);while (0 <= i - k - 1 && i + k < n && s[i - k - 1] == s[i + k]) {k++;}d2[i] = k--;if (i + k > r) {l = i - k - 1;r = i + k;}
}

9.ST表板子類似歸并的有條理暴力 sparse-table

1.原理是“倍增”，直到兩個長度為1的就可以合成一個長度為2的，兩個2合成4，兩個4合成8。

2.最后使用時沒必要追求“正好匹配”，可以在范圍內取多點：

比如看4_{8長度為5（45678），我們取長度為4，看4}7與5~8的最大值哪個更大即可。

ST表部分的代碼：

//ST表vector<vector<int>>st(30,vector<int>(n+1));//len = 2的i次方int len = 1;for (int pow = 0; len <= n; pow++, len *=2){for (int left = 1; left <= n- len+1; left++){if (pow == 0)st[0][left] = arr[left];else{st[pow][left] = max(st[pow - 1][left], st[pow - 1][min(left + len / 2,n)]);}}}

使用示范：

void solve()
{int n, m;cin >> n >> m;vector<int>arr(n+1);for (int i = 1; i <= n; i++){cin >> arr[i];}//ST表vector<vector<int>>st(30,vector<int>(n+1));//len = 2的i次方int len = 1;for (int pow = 0; len <= n; pow++, len *=2){for (int left = 1; left <= n- len+1; left++){if (pow == 0)st[0][left] = arr[left];else{st[pow][left] = max(st[pow - 1][left], st[pow - 1][min(left + len / 2,n)]);}}}for (int i = 1; i <= m; i++){int l, r;cin >> l >> r;//l+len-1<=r	len = 2的k次方//len <= r-l+1//k <= log(r-l+1);int k = log2(r - l + 1);cout << max(st[k][l], st[k][r-pow(2,k)+1]) << endl;}
}

10.LCA倍增板子

預處理：

void solve()
{int n, k;cin >> n >> k;vector<vector<int>>alist(n + 1);for (int i = 1; i <= n - 1; i++){int x, y;cin >> x >> y;alist[x].push_back(y);alist[y].push_back(x);}vector<vector<int>>fa(n + 1, vector<int>(22));vector<int>dep(n + 1);vector<int>leaf;auto dfs = [&](int cur, int pa, auto dfs)->void {dep[cur] = dep[pa] + 1;if (alist[cur].size() == 1){leaf.push_back(cur);}for (auto x : alist[cur]){if (x != pa){fa[x][0] = cur;dfs(x, cur, dfs);}}};dfs(1, 0, dfs);//倍增求父親for (int p = 1; p < 22; p++){for (int i = 1; i <= n; i++){fa[i][p] = fa[fa[i][p - 1]][p - 1];}}

LCA:

auto LCA = [&](int a, int b)->pair<int, int>
{ll ans = 0;if (dep[a] < dep[b])swap(a, b);while (dep[a] > dep[b]){int dis = (int)log2(dep[a] - dep[b]);a = fa[a][dis];ans += pow(2, dis);}for (int i = log2(dep[a]); i >= 0; i--){if (fa[a][i] != fa[b][i])	//向上結果不同才跳{a = fa[a][i];b = fa[b][i];ans += pow(2, i) * 2;}}if (a != b){a = b = fa[a][0];ans += 2;}return { a ,ans };
};

第一個讓a，b深度相同的操作是while進行的，二進制拆分。

主函數外版：

inline int LCA(int a,int b)
{if (dep[a] < dep[b])swap(a, b);while (dep[a] > dep[b]){int dis = (int)log2(dep[a] - dep[b]);a = fa[a][dis];}if (a == b)return a;for (int i = log2(dep[a]); i >= 0; i--){if (fa[a][i] != fa[b][i]){a = fa[a][i];b = fa[b][i];}}if (a != b){a = b = fa[a][0];}return a;
}

使用示范：（鏈式前向星等，POJ 3417 Network 樹上差分 LCA 鏈式前向星仍超時，加上快讀過-CSDN博客）

struct node
{int b, next;
}edges[maxn*2];
int head[maxn];
int k = 0;
inline void add(int a, int b)
{k++;edges[k].b = b;edges[k].next = head[a];head[a] = k;
}
int fa[maxn][23];
int dep[maxn];
void dfs1(int cur ,int pa)
{dep[cur] = dep[pa] + 1;fa[cur][0] = pa;for (int p = 1; p < 22; p++)fa[cur][p] = fa[fa[cur][p - 1]][p - 1];for (int i = head[cur]; i > 0; i = edges[i].next){if(edges[i].b != pa)dfs1(edges[i].b, cur);}
}
inline int LCA(int a,int b)
{if (dep[a] < dep[b])swap(a, b);while (dep[a] > dep[b]){int dis = (int)log2(dep[a] - dep[b]);a = fa[a][dis];}if (a == b)return a;for (int i = log2(dep[a]); i >= 0; i--){if (fa[a][i] != fa[b][i]){a = fa[a][i];b = fa[b][i];}}if (a != b){a = b = fa[a][0];}return a;
}
int diff[maxn];
int pass[maxn];
int cnt0, cnt1;
void dfs2(int cur,int pa)
{pass[cur] += diff[cur];for (int i = head[cur]; i > 0; i = edges[i].next){if (edges[i].b != pa){dfs2(edges[i].b, cur);pass[cur] += pass[edges[i].b];}}
}

11.KMP板子前綴跳后綴

原理：

出現重復【存在部分前綴等于后綴（自己的前面一部分跟后面一部分一樣的）】的時候，可以跳！
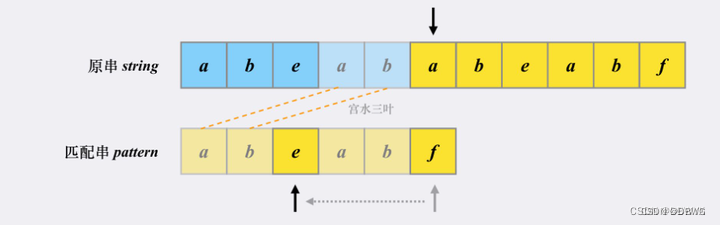
請添加圖片描述

來源：KMP算法中next數組的理解 - 知乎 (zhihu.com)

（其實原理好懂，實現起來是有些難度的。）

板子：

kmp的返回值可以自己選擇，比如第一次匹配成功返回位置，或者返回能匹配的數量。

//kmp
int kmp(vector<int> next, string str1, int len1, string str2, int len2)
{int i = 0, j = 0;int count = 0;while (i < len1){if (j == -1 || str1[i] == str2[j]){i++; j++;}elsej = next[j];if (j == len2){count++;// //最后一個比完后進來這個位置//return i - len2 + 1;//"第幾個位置"//cout << i - len2 + 1 << endl;i--;j--;j = next[j];}}return count;
}//next
void get_next(vector<int>& next, string str2, int len2)
{int i = 0, j = -1;next[0] = -1;while (i < len2){if (j == -1 || str2[i] == str2[j]){i++, j++;next[i] = j;}elsej = next[j];}
}

12.掃描線板子小思路

前言：

本板子是結合我的線段樹1板子和OIWIKI的掃描線寫成的類。

線段樹1板子區間加-CSDN博客

掃描線 - OI Wiki (oi-wiki.org)

背景：

照著OI WIKI打了一遍，結果洛谷交上去RE，查了半天查不出來，最后看討論區，給線段樹大小再乘個2，就過了。。

我還數組以為太大了呢

本題數組并不大：
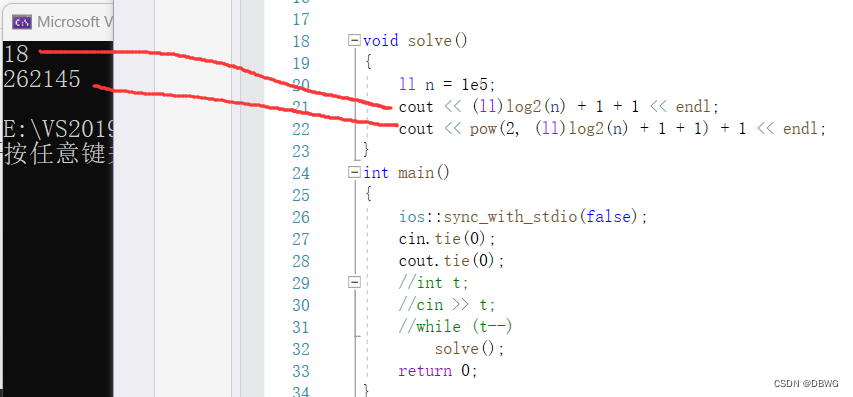
請添加圖片描述

本題的xy是坐標，看的是坐標間的長度，應該是線段樹進行二分的時候都要有mid，所以會多分幾次。

掃描線原理：

我們從下往上掃吧。

離散化就是把出現的x坐標放到數組里，排好序，數組里只有我們要的x。

離散化x后對這個數組進行建樹。

然后我們從下往上是根據y坐標進行的，所以每個y捆綁對應的x1,x2,以及加或減。

//這就是整個策略了。

代碼：

#define ll long long
#define endl "\n"
#define int long long
const ll inf = 1e9;template<class T>
class ST//segment tree
{struct node{T l, r, sum;T t;//懶標記//服務后代node() :l(0), r(0), sum(0), t(0){}};ll n;vector<T>a;vector<node>d;//掃描線中，上面的node中的l,r代表矩形左右//下面的l,r是線段樹的下標，每個a表示的是一個橫坐標
public:void push_up(ll i){if (d[i].t > 0)//掃描到了d[i].sum = d[i].r - d[i].l;elsed[i].sum = d[i * 2].sum + d[i * 2 + 1].sum;}//直到最左和最右范圍，但是不知道其中的和void build_tree(ll i, ll l, ll r){ll mid = l + (r - l) / 2;if (l + 1 < r){d[i].l = a[l];d[i].r = a[r];build_tree(i * 2, l, mid);build_tree(i * 2 + 1, mid, r);push_up(i);}else{d[i].l = a[l];d[i].r = a[r];d[i].sum = 0;}}void update(ll l, ll r, ll val){_update(1, l, r, val);//加并掛標記}void _update(ll i, ll l, ll r, ll val){if (d[i].l == l && d[i].r == r){d[i].t += val;push_up(i);return;}else{//中分if (d[i * 2].r > l)_update(i * 2, l, min(d[i * 2].r, r), val);//r在下一個內就不多傳了if (d[i * 2 + 1].l < r)_update(i * 2 + 1, max(l, d[i * 2 + 1].l), r, val);push_up(i);}}T get_sum(){return d[1].sum;}ST(vector<T>arr){a = arr;n = a.size() - 1;d = vector<node>(2*pow(2, (ll)log2(n) + 1 + 1) + 1);build_tree(1, 1, n);}
};
struct scanline
{int l, r, h;int mark;bool operator <(const scanline b)const{return h < b.h;}
};
//總的sum統計了此刻矩形的長度，update一直在更新這個長度
void solve()
{int n; cin >> n;vector<int>xaxis;vector<scanline>yaxis;//x離散化用來服務線段樹//y該多少個就多少個，遇到就改，離散化了求得高度差，同層是0//該加加，該減減，區間求和改成求長度吧xaxis.push_back(0);yaxis.push_back({});for (int i = 1; i <= n; i++){int x1, y1, x2, y2;cin >> x1 >> y1 >> x2 >> y2;xaxis.push_back(x1);xaxis.push_back(x2);yaxis.push_back({ x1,x2,y1,1 });yaxis.push_back({ x1,x2,y2,-1 });}sort(xaxis.begin() + 1, xaxis.end());sort(yaxis.begin() + 1, yaxis.end());unique(xaxis.begin() + 1, xaxis.end());ST<int> demo(xaxis);int ans = 0;for (int i = 1; i < yaxis.size() - 1; i++)//最后一次不用算了{demo.update(yaxis[i].l, yaxis[i].r, yaxis[i].mark);ans += demo.get_sum() * (yaxis[i + 1].h - yaxis[i].h);}cout << ans;
}
signed main()
{ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);int t = 1;//cin >> t;while (t--){solve();}return 0;
}

13.龜速乘板子 a*二進制拆分的正數b（mod p）

如果要乘負數b，先乘正的，最后結果加負號即可。

ll mul(ll a, ll b, ll p) {// 將乘法變為加法，二進制優化，邊加邊模ll ans = 0;while (b) {if (b & 1)ans = (ans + a) % p;a = (a + a) % p;b >>= 1;}return ans;
}

14.拓展歐幾里得法求逆元

板子：

x即為最終答案，x可能為負數，加模數即可

乘法逆元 - OI Wiki (oi-wiki.org)

void exgcd(int a, int b, int& x, int& y) {if (b == 0) {x = 1, y = 0;return;}exgcd(b, a % b, y, x);y -= a / b * x;
}

使用:

	exgcd(a, n + 1, x, y);//x就是逆元while (x <= 0)x += n + 1;

原理：

最大公約數 - OI Wiki (oi-wiki.org)
請添加圖片描述

拓展歐幾里得算法：

int Exgcd(int a, int b, int &x, int &y) {if (!b) {x = 1;y = 0;return a;}int d = Exgcd(b, a % b, x, y);int t = x;x = y;y = t - (a / b) * y;return d;
}

15.二分圖板子匈牙利算法 KM算法

KM算法

原理：

匈牙利算法：二分圖最大權匹配 - OI Wiki

簡單說就是挨個找，找到就退出。后面的來了就讓前面的挪位置。

板子：

book指給u找位置時，有人考慮過的位置就不考慮了。

match[ i ]就是i位置對應的人。

e是關系

int book[10001];
int match[10001];
bool e[101][101];
int ans=0,n=0,m=0;
bool dfs(int u)
{for(int i=1;i<=n;i++){if(book[i]==0 && e[u][i]==true){book[i]=1;if(match[i]==0 || dfs(match[i])==true){match[u]=i;match[i]=u;return true;}}}return false;
}

使用：

int main()
{scanf("%d %d",&n,&m);for(int i=1;i<=m;i++){int x=0,y=0;scanf("%d %d",&x,&y);e[x][y]=true;e[y][x]=true;}for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){book[j]=0;}if(dfs(i)==true){ans++;}}printf("%d",ans);return 0;
}

16.盧卡斯定理/Lucas定理板子組合數板子

a是階乘數組，提前處理好，處理到模數應該夠的。

ksm快速冪

C是組合數函數，ksm是用來費馬小定理求逆元（即倒數）。就是組合數公式，n的階乘除以（m的階乘和n-m的階乘）。

Lucas 盧卡斯定理 - OI Wiki (oi-wiki.org)

ll a[100005];
ll ksm(int x, int y,int mod) {//因為數據范圍很大容易爆掉，所以就要Fast_Powif (x == 1) return 1;ll res = 1, base = x;while (y) {if (y & 1) res = (res * base) % mod;base = (base * base) % mod;y >>= 1;}return res;
}ll C(ll n, ll m,ll p) 
{if (m > n)return 0;return ((a[n] * ksm(a[m], p - 2, p)) % p * ksm(a[n - m], p - 2, p) % p);
}long long Lucas(long long n, long long m, long long p) 
{if (m == 0) return 1;return (C(n % p, m % p, p) * Lucas(n / p, m / p, p)) % p;
}

17.高精度加法，乘法板子

High precision addition

string hpa(string str1,string str2)
{int a[10000] = { 0 }, b[10000] = { 0 }, c[10000] = { 0 };int len1 = str1.size(), len2 = str2.size();//`len1>=len2if (len2 > len1)swap(str1, str2), swap(len1, len2);for (int i = 0; i < len1; i++)a[i] = str1[len1-1-i] - '0';for (int i = 0; i < len2; i++)b[i] = str2[len2-1-i] - '0';for (int i = 0; i < len1; i++){c[i + 1] = (a[i] + b[i] + c[i])/10;c[i] = (c[i] + a[i] + b[i]) % 10;}if (c[len1] != 0)len1++;string ret;for (int i = len1 - 1; i >= 0; i--){ret += '0' + c[i];}return ret;
}

High precision multiplication

//     999
//     999
//----------
//    8991
//   8991
//  8991
//  123456
string hpm(string str1,string str2)
{int a[10000] = { 0 }, b[10000] = { 0 }, c[10000] = { 0 };int len1 = str1.size(), len2 = str2.size();for (int i = 0; i < len1; i++)a[i] = str1[len1 - 1 - i] - '0';for (int i = 0; i < len2; i++)b[i] = str2[len2 - 1 - i] - '0';for (int i = 0; i < len1; i++){for (int j = 0; j < len2; j++){c[i + j] += a[i] * b[j];//也可以順便在最后處理}}int len = len1 + len2;for (int i = 0; i < len; i++){c[i + 1] += c[i] / 10;c[i] = c[i] % 10;}while (c[len - 1] == 0&&len>1/**/){len--;}string ret;for (int i = len - 1; i >= 0; i--){ret += '0' + c[i];}return ret;
}

18.排列組合板子 A C

a是階乘數組，預處理一下

ksm快速冪求的是逆元。用的是費馬小定理，適用于模數為素數的時候。

ll ksm(int x, int y, int mod) 
{if (x == 1) return 1;ll res = 1, base = x;while (y) {if (y & 1) res = (res * base) % mod;base = (base * base) % mod;y >>= 1;}return res;
}
ll C(ll n, ll m, ll p)
{if (m > n)return 0;return ((a[n] * ksm(a[m], p - 2, p)) % p * ksm(a[n - m], p - 2, p) % p);
}
ll A(ll n, ll m, ll p)
{if (m > n)return 0;return (a[n] * ksm(a[n - m], p - 2, p)) % p;
}

19.快讀快寫板子

inline int read()
{int x = 0, f = 1;char ch = getchar();while (ch < '0' || ch>'9'){if (ch == '-')f = -1;ch = getchar();}while (ch >= '0' && ch <= '9'){x = (x << 1) + (x << 3) + (ch ^ 48);ch = getchar();}return x * f;
}
inline void write(int x)
{if (x < 0){putchar('-');x = -x;}if (x > 9)write(x / 10);putchar(x % 10 + '0');
}

20.分解質因數板子

vector<int>divide(int x)
{vector<int>ret;for (int i = 2; i <= x / i; i++)//i*i <= x {if (x % i == 0){ret.push_back(i);while (x % i == 0)x /= i;}}if (x > 1)ret.push_back(x);return ret;
}

21.快速選擇數組中的第K個最大元素

class Solution {int _k;
public:// [0,l][l+1,r-1][r,nums.size()-1]int _sort(int left,int right,vector<int>& nums){if(left==right)return nums[left];int aim = getRandom(left,right,nums);int i = left,l = left-1,r = right+1;while(i<r){if(nums[i]<aim)swap(nums[++l],nums[i++]);else if(nums[i] == aim)i++;else swap(nums[--r],nums[i]);}if(nums.size()-1-r+1>=_k)return _sort(r,right,nums);else if(nums.size()-1-(l+1)+1>=_k)return nums[i-1];elsereturn _sort(left,l,nums);}int getRandom(int left,int right,vector<int>& nums){int r = rand();return nums[r%(right-left+1) + left];/*    偏移量   */}int findKthLargest(vector<int>& nums, int k) {srand(time(NULL));_k = k;return _sort(0,nums.size()-1,nums);}
};

22. 26個質數

int arr[26] = {2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79,83,89,97,101};

23.多重背包問題

const int MAX = 1e3 + 5;
int v[MAX], w[MAX], s[MAX];
int main()
{ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);int N, V;cin >> N >> V;for (int i = 1; i <= N; i++){cin >> w[i] >> v[i] >> s[i];}int dp[MAX] = { 0 };for (int i = 1; i <= N; i++){if (s[i] == -1){for (int j = V; j >= w[i]; j--){dp[j] = max(dp[j], dp[j - w[i]]+v[i]);}}else if (s[i] == 0){for (int j = w[i]; j <= V; j++){dp[j] = max(dp[j], dp[j - w[i]] + v[i]);}}else if (s[i] > 0){int num = min(s[i], V/w[i]);for (int k = 1;num>0; k <<= 1){if (num < k)k = num;num -= k;for (int j = V; j >= w[i] * k; j--){dp[j] = max(dp[j], dp[j-w[i]*k]+v[i]*k);}}}}cout << dp[V];return 0;
}

24.歸并

class Solution {int marr[50005];
public:void merge(int left,int right,vector<int>&arr){if (left >= right)return;int mid = (left + right)>>1;//3 /2  + 5/2merge(left, mid,arr);merge(mid+1, right,arr);int aim = left;int part1 = left, part2 = mid + 1;while (part1<=mid && part2<=right){if (arr[part1] <= arr[part2])marr[aim++] = arr[part1++];elsemarr[aim++] = arr[part2++];}while (part1 <= mid)marr[aim++] = arr[part1++];while (part2 <= right)marr[aim++] = arr[part2++];//最后再賦回去。。for (int i = left; i <= right; i++)arr[i] = marr[i];}vector<int> sortArray(vector<int>& nums) {merge(0,nums.size()-1,nums);return nums;}
};

25.判斷是素數質數

bool is_prime(int x)
{for(int i = 2; i * i <= x; i++){if (x % i == 0)return false;}return true;
}

26.素數篩法

Eratosthenes 篩法（埃拉托斯特尼篩法，簡稱埃氏篩法）篩至平方根

考慮這樣一件事情：對于任意一個大于 1 的正整數 n，那么它的 x 倍就是合數（x > 1）。利用這個結論，我們可以避免很多次不必要的檢測。

如果我們從小到大考慮每個數，然后同時把當前這個數的所有（比自己大的）倍數記為合數，那么運行結束的時候沒有被標記的數就是素數了。

vector<int> prime;
bool is_prime[N];void Eratosthenes(int n) {is_prime[0] = is_prime[1] = false;for (int i = 2; i <= n; ++i) is_prime[i] = true;// i * i <= n 說明 i <= sqrt(n)for (int i = 2; i * i <= n; ++i) {if (is_prime[i])for (int j = i * i; j <= n; j += i) is_prime[j] = false;}for (int i = 2; i <= n; ++i)if (is_prime[i]) prime.push_back(i);
}

分塊篩選

int count_primes(int n) {const int S = 10000;vector<int> primes;int nsqrt = sqrt(n);vector<char> is_prime(nsqrt + 1, true);for (int i = 2; i <= nsqrt; i++) {if (is_prime[i]) {primes.push_back(i);for (int j = i * i; j <= nsqrt; j += i) is_prime[j] = false;}}int result = 0;vector<char> block(S);for (int k = 0; k * S <= n; k++) {fill(block.begin(), block.end(), true);int start = k * S;for (int p : primes) {int start_idx = (start + p - 1) / p;int j = max(start_idx, p) * p - start;for (; j < S; j += p) block[j] = false;}if (k == 0) block[0] = block[1] = false;for (int i = 0; i < S && start + i <= n; i++) {if (block[i]) result++;}}return result;
}

線性篩法

也稱為 Euler 篩法（歐拉篩法）

vector<int> pri;
bool not_prime[N];void pre(int n) {for (int i = 2; i <= n; ++i) {if (!not_prime[i]) {pri.push_back(i);}for (int pri_j : pri) {if (i * pri_j > n) break;not_prime[i * pri_j] = true;if (i % pri_j == 0) {// i % pri_j == 0// 換言之，i 之前被 pri_j 篩過了// 由于 pri 里面質數是從小到大的，所以 i 乘上其他的質數的結果一定會被// pri_j 的倍數篩掉，就不需要在這里先篩一次，所以這里直接 break// 掉就好了break;}}}
}