思路

難點1
如何理解特殊字符 ’ * ’ 的作用？
如何正確的利用特殊字符 ’ . ’ 和 ’ * ’ ？

'*' 匹配零個或多個前面的那一個元素
"a*" 可表示的字符為不同數目的 'a'，包括：
""（0 個 'a'）
"a"（1 個 'a'）
"aa"（2 個 'a'）
"aaa"（3 個 'a'）

難點2
正則表達式匹配:一種在文本中查找特定模式的方法。
這道題的正則匹配規則主要是 ’ * '、 ’ . ’ 這兩個特殊字符的使用。

如何利用現有數據結構 構造這個問題？
按照規則，（有順序）從左到右來匹配一個字符串。
所謂匹配，是要涵蓋 整個 字符串 s的，而不是部分字符串。

如果不考慮這兩個特殊字符，我們可以用二維數組來動態的表示兩個字符串是否匹配。只有前面的數組匹配上，后面的數組才可以繼續匹配。

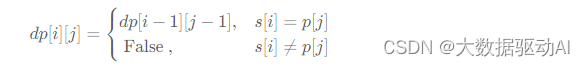
但現在要考慮 ’ * '、 ’ . ’ 這兩個特殊字符。
p[j]= ‘.’，則 p[j]一定可以與 s[i]匹配成功，此時有dp[i][j]=dp[i?1][j?1]
p[j]= ‘*’，則表示可對 p[j]的前一個字符 p[j?1]匹配（或理解為復制）任意次（包括 0 次）。

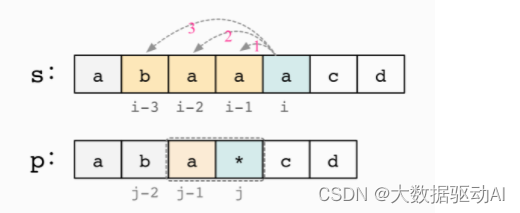
匹配0次，意味著 p[j?1]和 p[j]不起作用，
相當于在 p 中刪去了 p[j?1]和 p[j]，
此時有：dp[i][j]=dp[i][j?2]

匹配 1次，意味著 p[j?1]和 p[j]組成了 1 個’a’，若 s[i?1+1, …, i]=p[j?1]，
則 dp[i][j]可由 dp[i?1][j?2]轉移而來，
此時有：dp[i][j]=dp[i?1][j?2],&s[i?1+1, …, i]=p[j?1]

匹配 k 次，意味著 p[j?1]和 p[j]組成了 k 個’a’，若 s[i?k+1, …, i]=p[j?1]，
則 dp[i][j]可由 dp[i?k][j?2]轉移而來，
此時有：dp[i][j]=dp[i?k][j?2],&s[i?k+1, …, i]=p[j?1]

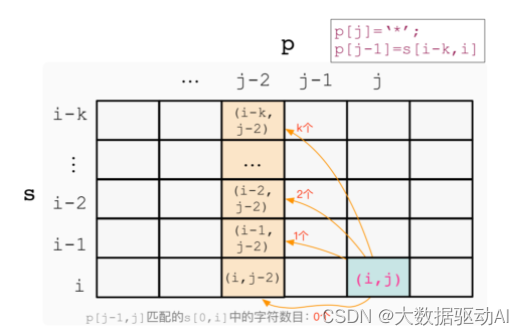
難點3
狀態轉移的優化
總的來看，當 p[j]= '’ 時，對于匹配 0～k次，我們有：

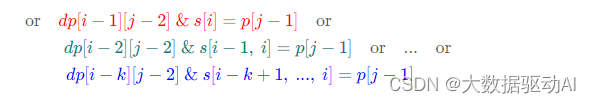
同時，對于 dp[i?1][j]我們有：

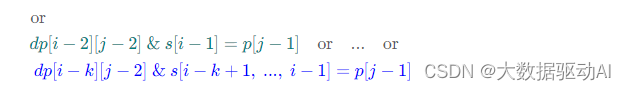
觀察發現，（2）式與（1）式中的后 k 項剛好相差了一個條件 s[i]=p[j?1]，將（2）式代入（1）式可得簡化后的「狀態轉移方程」為：
p[j]= ''時，簡化后對應的狀態更新過程如下圖所示：

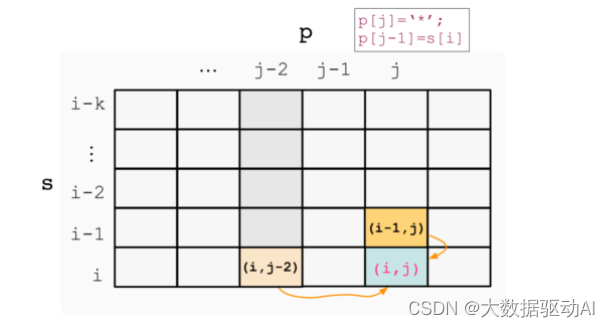
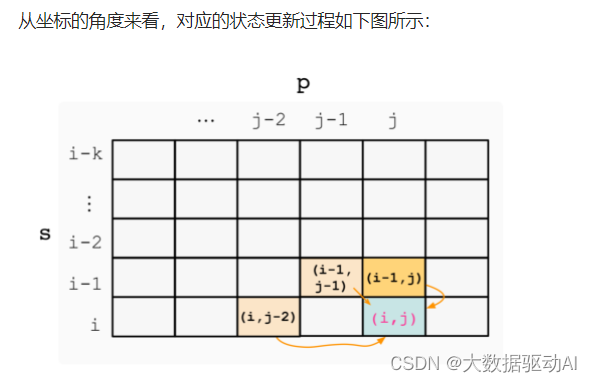
記 s 的長度為 m，p的長度為 n 。為便于狀態更新，減少對邊界的判斷，初始二維 dpdpdp 數組維度為 (m+1)×(n+1)，其中第一行和第一列的狀態分別表示字符串 s 和 p 為空時的情況。

顯然，dp[0][0]=True。對于其他 dp[0][j]，當 p[j]≠p[j]='‘時，s[0,…,j]無法與空字符匹配，因此有 dp[0][j]=False；而當 p[j]=p[j]=p[j]=’'時，則有 dp[0][j]=dp[0][j?2]。

python

class Solution:def isMatch(self, s: str, p: str) -> bool:m, n = len(s), len(p)dp = [[False] * (n+1) for _ in range(m+1)]# 初始化dp[0][0] = Truefor j in range(1, n+1):if p[j-1] == '*':dp[0][j] = dp[0][j-2]# 狀態更新for i in range(1, m+1):for j in range(1, n+1):if s[i-1] == p[j-1] or p[j-1] == '.':dp[i][j] = dp[i-1][j-1]elif p[j-1] == '*':     # 【題目保證'*'號不會是第一個字符，所以此處有j>=2】if s[i-1] != p[j-2] and p[j-2] != '.':dp[i][j] = dp[i][j-2]else:dp[i][j] = dp[i][j-2] | dp[i-1][j]return dp[m][n]