目錄

摘要

一、文獻閱讀

1、題目

2、摘要

3、模型架構

4、文獻解讀

一、Introduction

二、實驗

三、結論

二、PINN

一、PINN比傳統數值方法有哪些優勢

二、PINN方法

三、正問題與反問題

三、PINN實驗

一、數學方程

二、模型搭建

總結

摘要

本周我閱讀了一篇題目為Deep Residual Learning for Image Recognition的文獻，文章的貢獻是作者提出了殘差網絡的思想，且證明了更深層的殘差網絡具有比VGG網絡更低的復雜度和更高的準確性，同時，殘差網絡實現了更容易的訓練過程。其次，對PINN進行了繼續的學習，PINN?是一種科學機器在傳統數值領域的應用方法，特別是用于解決與偏微分方程相關的各種問題，包括方程求解、參數反演、模型發現、控制與優化等。

This week, I read a paper titled "Deep Residual Learning for Image Recognition." The contribution of the paper is that the author introduces the concept of residual networks and demonstrates that deeper residual networks have lower complexity and higher accuracy compared to VGG networks. Additionally, residual networks achieve a more straightforward training process. Furthermore, I gained preliminary insights into Physics-Informed Neural Networks (PINN). PINN is an application of scientific machine learning in traditional numerical domains, particularly for solving various problems related to partial differential equations. This includes equation solving, parameter inversion, model discovery, control, and optimization.

一、文獻閱讀

1、題目

題目：Deep Residual Learning for Image Recognition??

鏈接：https://arxiv.org/abs/1512.03385

2、摘要

本文展示了一種殘差學習框架，能夠簡化使那些非常深的網絡的訓練，該框架使得層能根據其輸入來學習殘差函數而非原始函數。作者提出了殘差網絡的思想，且證明了更深層的殘差網絡具有比VGG網絡更低的復雜度和更高的準確性。同時，殘差網絡實現了更容易的訓練過程。

This article presents a residual learning framework that simplifies the training of very deep networks. The framework allows layers to learn residual functions based on their inputs rather than the original functions. The author introduces the concept of residual networks and demonstrates that deeper residual networks have lower complexity and higher accuracy compared to VGG networks. Additionally, residual networks achieve a more straightforward training process.

?

3、模型架構

Plain Network
受VGG網絡的影響，plain網絡（如下圖中間）的卷積層主要是3*3的濾波器，加權層的層數為34，在網絡的最后是全局的平均pooling層和一個1000種類的包含softmax函數的全連接層。plain網絡比VGG網絡有更少的濾波器（卷積核后面的64，128，256等代表個數）和更低的計算復雜度，VGG-19模型有196億個FLOPS，plain網絡含有36億個FLOPS。
Residual Network
在plain網絡的基礎上，加入shortcut連接，就變成了相應的殘差網絡，上圖中所加實線表明可以直接使用恒等shortcuts，虛線表示維度不匹配時的情況，需要先調整維度再相加，調整維度的方法有兩種：（A)仍然使用恒等映射，只是在增加的維度上使用0來填充，這種方法不會引入額外的參數；(B)使用1x1的卷積映射shortcut來調整維度保持一致。這兩種方法都使用stride為2的卷積。

4、文獻解讀

一、Introduction

神經網絡模型的深度對訓練任務起著至關重要的作用，但是當模型深度太大時，會存在梯度消失/梯度爆炸的問題，盡管normalized initial-ization和intermediate normalization可以在一定程度上解決這個問題，但是準確率依然會在達到飽和后迅速退化，因此錯誤率甚至會更高，如下圖所示，越深的網絡有越高的訓練錯誤率和測試錯誤率。
?

文章提出了深度殘差學習（deep residual learning）框架來解決上圖中的問題，如下圖所示，通過前饋神經網絡的shortcut connections來跨過一個層或者多個層，將前層的輸出直接與卷積層的輸出疊加，相當于做了個恒等映射。在極端情況下，如果恒等映射最優，可以將殘差設置為0就簡單地實現了恒等映射。簡單來說，殘差學習就是將一層的輸入與另一層的輸出結果一起作為一整個塊的輸出。

ResNet?之所以叫殘差網絡（Residual Network），是因為 ResNet 是由很多殘差塊（Residual Block）組成的。而殘差塊的使用，可以解決前面說到的退化問題。殘差塊如下圖所示。

殘差（residual）在數理統計中是指實際觀察值（觀測值）與估計值（擬合值）之間的差。
假設上圖中的 weight layer 是 3×3 的卷積層；F(x) 表示經過兩個卷積層計算后得到的結果；identity x 表示恒等映射（identity?mapping），也稱為shortcut connections。其實就是把 x 的值是不做任何處理直接傳過去。最后計算 F(x)+x，這里的 F(x) 跟 x 是種類相同的信號，所以將其對應位置進行相加。我們讓 H(x) = F(x)+x ，所以 H(x) 就是觀測值，x 就是估計值。
我們如果使用plain networks（一般的卷積神經網絡）那么 H(x) = F(x) ?，這樣某一層達到最優之后在加深就會出現退化問題。殘差就體現在：F(x) = H(x)-x ?，我們假設優化殘差映射比優化原始的、未引用殘差的映射更容易。在極端情況下，如果一個恒等映射 x 是最優的，那么將殘差 F(x) 推到 0 比通過一堆非線性層來擬合一個恒等映射要容易得多。

二、實驗

1、數據集

數據集：ImageNet 2012 classifi-cation dataset（1000類）
數據量：128 萬張訓練圖像，5萬張測試圖像
標準：評估 top-1 和 top-5 錯誤率

2、參數設置

從一張圖像或者它的水平翻轉圖像中隨機采樣一個224*224的crop，每個像素都減去均值。圖像使用標準的顏色增強。我們在每一個卷積層之后，激活層之前均使用batch normalization（BN）。我們根據He2014spatial來初始化權值然后從零開始訓練所有plain/殘差網絡。
我們使用的mini-batch的尺寸為256。學習率從0.1開始，每當錯誤率平穩時將學習率除以10，整個模型進行次迭代訓練。我們將權值衰減設置為0.0001，a 動量為0.9。

3、實驗結果

普通網絡，結論：
（1）較深的 34 層普通網絡比較淺的 18 層普通網絡具有更高的驗證誤差。34 層普通網絡在整個訓練過程中具有較高的訓練誤差，盡管 18 層普通網絡的解空間是 34 層網絡的子空間。
（2）論文認為這種優化困難不是由梯度消失引起的。這些普通網絡使用 BN 進行訓練，確保前向傳播的信號具有非零方差。我們還驗證了反向傳播的梯度在 BN 中表現出健康的范數。所以前向和后向信號都不會消失。事實上，34 層的普通網絡仍然能夠達到有競爭力的精度（表 3），這表明求解器在一定程度上起作用。我們推測深的普通網絡的收斂速度可能呈指數級低，這會影響訓練誤差的減少。

ResNet，結論：
（1）34 層 ResNet 優于 18 層 ResNet（提高 2.8%）。更重要的是，34 層的 ResNet 表現出相當低的訓練誤差，并且可以推廣到驗證數據。這表明退化問題在此設置中得到了很好的解決，可以通過增加深度來獲得準確度。
（2）相比普通網絡ResNet 將 top-1 誤差降低了 3.5%（表 2），這是由于成功降低了訓練誤差。這種比較驗證了殘差學習在極深系統上的有效性。
（3）我們還注意到 18 層的普通/殘差網絡相當準確，但 18 層的 ResNet 收斂速度更快。當網絡“不太深”（此處為 18 層）時，當前的 SGD 求解器仍然能夠為普通網絡找到好的解決方案。在這種情況下，ResNet 通過在早期提供更快的收斂來簡化優化。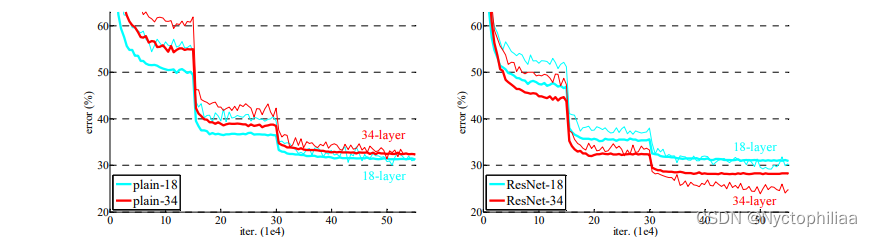

三、結論

殘差結構的主要作用是傳遞信號，把深度學習淺層的網絡信號直接傳給深層的網絡。深度學習中不同的層所包含的信息是不同的，一般我們認為深層的網絡所包含的特征可能對最后模型的預測更有幫助，但是并不是說淺層的網絡所包含的信息就沒用，深層網絡的特征就是從淺層網絡中不斷提取而得到的。現在我們給網絡提供一個捷徑，也就是Shortcut Connections，它可以直接將淺層信號傳遞給深層網絡，跟深層網絡的信號結合，從而幫助網絡得到更好的效果。
?

二、PINN

一、PINN比傳統數值方法有哪些優勢

PINN是一種（深度）網絡，在定義時空區域中給定一個輸入點，在訓練后在微分方程的該點中產生估計的解。結合對控制方程的嵌入得到殘差，利用殘差構造損失項。本質原理就是將方程（物理知識）集成到網絡中，并使用來自控制方程的殘差項來構造損失函數，由該項作為懲罰項來限制可行解的空間。用PINN來求解方程并不需要有標簽的數據，比如先前模擬或實驗的結果。PINN算法本質上是一種無網格技術，通過將直接求解控制方程的問題轉換為損失函數的優化問題來找到偏微分方程解。

1、傳統數值方法主要針對復雜問題的正計算，比如說已知邊界條件、已知控制方程的正計算，在正計算上，深度學習的方法遜色一些，但是針對一些反問題，比如說一些測量數據和部分物理(方程中某些參數未知、邊界條件未知)，深度學習方法可以形成數據和物理雙驅動的模型，比傳統數值方法的效率更高。

2、當面對一些數值問題時，PINN可以不需要用數值格式去推導求解，可以直接利用加物理損失的方法得到一個參考解，當問題邊界需要不停地換時，或者很多資源不停的變化的情況下，如果利用大量時間去訓練一個網絡，在推斷階段可以實現快速預測。

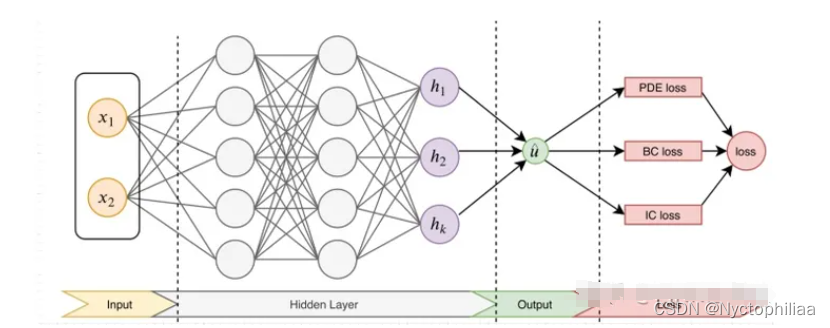
二、PINN方法

先構建一個輸出結果為?的神經網絡，將其作為PDE解的代理模型，將PDE信息作為約束，編碼到神經網絡損失函數中進行訓練。損失函數主要包括4部分：偏微分結構損失(PDE loss)，邊值條件損失(BC loss)、初值條件損失(IC loss)以及真實數據條件損失(Data loss)。

?

后，利用梯度優化算法最小化損失函數，直到找到滿足預測精度的網絡參數?。

對于逆問題(即方程中的某些參數未知)，若只知道PDE方程及邊界條件，PDE參數未知，該問題為非定問題，所以必須要知道其他信息，如部分觀測點u的值。此時，PINN做法可將方程中的參數作為未知變量，加到訓練器中進行優化，損失函數包括Data loss。

三、正問題與反問題

正問題和反問題的正經定義可以解釋為：正問題，已知原因，根據已有的模型和規律，得到結果狀態或者觀測，而反問題則是已知結果狀態或者觀測，來反推原因。正問題例子包括設計飛機的方案參數，然后通過模擬，可以知道飛機的性能，反問題則是根據飛機的設計需求，反推應該給什么設計方案。因此，工程界通常稱正問題為模擬問題，反問題為設計問題。對于一個PDE方程，我們這樣來定義正問題，已知PDE方程，求解PDE方程在場域內的解為正問題；反問題我們定義為，已知一些場域內的觀測情況，來反推最優的PDE方程的系數/參數的值。?

對于PDE問題而言，PINN的正問題就是根據已有的PDE來求解場域內的解。建立一個神經網絡?，來學習PDE的特性。具體來說，就是建立時間坐標和空間坐標與解的映射，即：。

神經網絡的訓練需要一個目標函數，PDE方程其實就是一個損失函數，如果不滿足等式關系，就會產生損失，因此，把神經網絡的放進PDE里面獲取損失。

從數學角度看，和傳統的機器學習相比，它最大的不同就是在要求0階常數項與系統一致的基礎上，同時要求高階梯度項與系統一致。從泰勒展開的角度來看，它顯然具有更高的精度，因為它更滿足系統的高維特征。 從機器學習和問題的適配角度來看，采用神經網絡而不是別的機器學習方法也是非常有見地的設計，因為神經網絡的可微性帶來了梯度求解的可行性。求解正問題時，PINN完全不需要數據，只需要隨意在空間和時間步上采樣，然后讓PDE方程來評估神經網絡的建模是否準確；或者說真實數據是基于PDE損失函數的中間量。

PINN 解反問題的任務是需要反推出PDE中的各項的超參數。這個問題的設定意味著我們沒有真實可靠的PDE方程來做評判 ，因此，需要實際的觀測（場域的值）來提供損失函數。簡而言之，我們就是在一族的PDE中挑一個最合適的來擬合實際的系統。

三、PINN實驗

一、數學方程

使用一個最簡單的常微分方程：

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ??

????????????????????????????????????????????????????????????????

這個微分方程其實就是：

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ??

二、模型搭建

核心-使用最簡單的全連接層：

class Net(nn.Module):def __init__(self, NL, NN): # NL n個l（線性，全連接）隱藏層， NN 輸入數據的維數，# NL是有多少層隱藏層# NN是每層的神經元數量super(Net, self).__init__()self.input_layer = nn.Linear(1, NN)self.hidden_layer = nn.linear(NN,int(NN/2)) ## 原文這里用NN，我這里用的下采樣，經過實驗驗證，“等采樣”更優。更多情況有待我實驗驗證。self.output_layer = nn.Linear(int(NN/2), 1)def forward(self, x):out = torch.tanh(self.input_layer(x))out = torch.tanh(self.hidden_layer(out))out_final = self.output_layer(out)return out_final

?偏微分方程定義，也就是第一個公式：

def ode_01(x,net):y=net(x)y_x = autograd.grad(y, x,grad_outputs=torch.ones_like(net(x)),create_graph=True)[0]return y-y_x   # y-y' = 0

源碼：

import torch
import torch.nn as nn
import numpy as np
import matplotlib.pyplot as plt
from torch import autograd"""
用神經網絡模擬微分方程,f(x)'=f(x),初始條件f(0) = 1
"""class Net(nn.Module):def __init__(self, NL, NN): # NL n個l（線性，全連接）隱藏層， NN 輸入數據的維數，# NL是有多少層隱藏層# NN是每層的神經元數量super(Net, self).__init__()self.input_layer = nn.Linear(1, NN)self.hidden_layer = nn.Linear(NN,int(NN/2)) ## 原文這里用NN，我這里用的下采樣，經過實驗驗證，“等采樣”更優。更多情況有待我實驗驗證。self.output_layer = nn.Linear(int(NN/2), 1)def forward(self, x):out = torch.tanh(self.input_layer(x))out = torch.tanh(self.hidden_layer(out))out_final = self.output_layer(out)return out_finalnet=Net(4,20) # 4層 20個
mse_cost_function = torch.nn.MSELoss(reduction='mean') # Mean squared error 均方誤差求
optimizer = torch.optim.Adam(net.parameters(),lr=1e-4)  # 優化器def ode_01(x,net):y=net(x)y_x = autograd.grad(y, x,grad_outputs=torch.ones_like(net(x)),create_graph=True)[0]return y-y_x   # y-y' = 0# requires_grad=True).unsqueeze(-1)plt.ion()  # 動態圖
iterations=200000
for epoch in range(iterations):optimizer.zero_grad()  # 梯度歸0## 求邊界條件的損失函數x_0 = torch.zeros(2000, 1)y_0 = net(x_0)mse_i = mse_cost_function(y_0, torch.ones(2000, 1))  # f(0) - 1 = 0## 方程的損失函數x_in = np.random.uniform(low=0.0, high=2.0, size=(2000, 1))pt_x_in = autograd.Variable(torch.from_numpy(x_in).float(), requires_grad=True)  # x 隨機數pt_y_colection=ode_01(pt_x_in,net)pt_all_zeros= autograd.Variable(torch.from_numpy(np.zeros((2000,1))).float(), requires_grad=False)mse_f=mse_cost_function(pt_y_colection, pt_all_zeros)  # y-y' = 0loss = mse_i + mse_floss.backward()  # 反向傳播optimizer.step()  # 優化下一步。This is equivalent to : theta_new = theta_old - alpha * derivative of J w.r.t thetaif epoch%1000==0:y = torch.exp(pt_x_in)  # y 真實值y_train0 = net(pt_x_in) # y 預測值print(epoch, "Traning Loss:", loss.data)print(f'times {epoch}  -  loss: {loss.item()} - y_0: {y_0}')plt.cla()plt.scatter(pt_x_in.detach().numpy(), y.detach().numpy())plt.scatter(pt_x_in.detach().numpy(), y_train0.detach().numpy(),c='red')plt.pause(0.1)

結果展示：

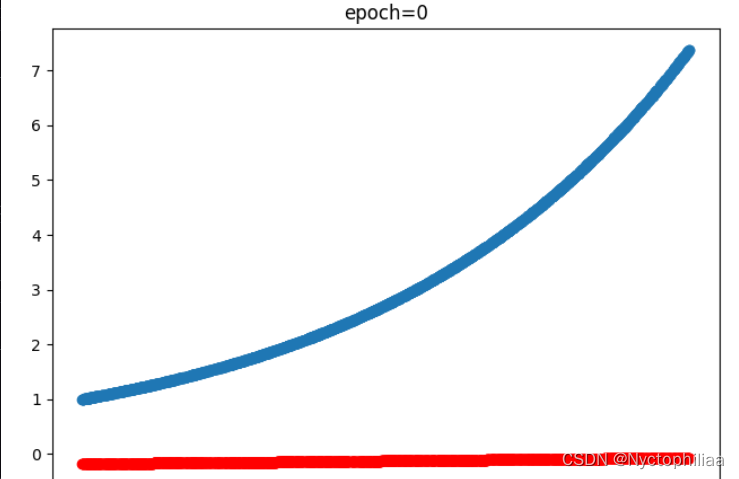
訓練0次時的結果也就是沒訓練，藍色是真實值、紅色是預測值：

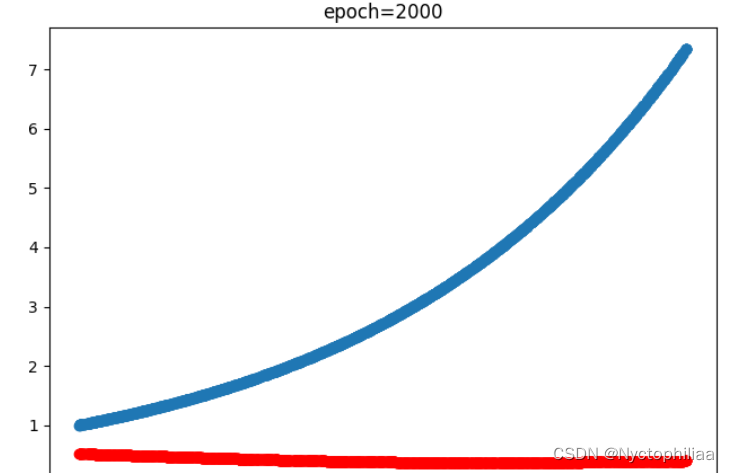
?訓練2000次時的結果，藍色是真實值、紅色是預測值：

訓練20000時的結果，藍色是真實值、紅色是預測值，不過紅色已經完全把藍色覆蓋了，也就是完全擬合了：

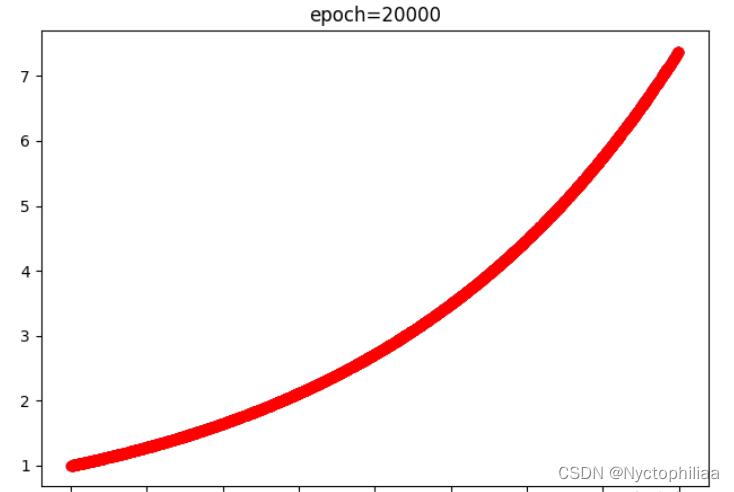
總結

ResNet網絡的最初原始論文說明：一味地加深網絡深度會使得網絡達到了一種飽和狀態（論文中強調不是過擬合現象，而是一種網絡深度到一定程度之后的退化問題），而導致精度的下降。PINN的原理就是通過訓練神經網絡來最小化損失函數來近似PDE的求解，所謂的損失函數項包括初始和邊界條件的殘差項，以及區域中選定點（按傳統應該稱為"配點"）處的偏微分方程殘差。

?