1、引言

小屌絲：魚哥，泡澡啊。
小魚：不去
小屌絲：… 此話當真？
小魚：此話不假
小屌絲：到底去還是不去？
小魚：我昨天剛泡完澡，今天還去？
小屌絲：… 你竟然自己去？
小魚：沒有啊

小屌絲：… 我不信，我不聽，反正你昨天去泡澡沒帶我。
小魚：…那待會咱倆再去唄
小屌絲： 這還差不多。嘿嘿~ ~
小魚：那等我一會
小屌絲：干啥啊這又？
小魚：當然是在忙嘍。
小屌絲：…

2、決策樹

2.1 定義

支持向量機（Support Vector Machine，簡稱SVM）是一種分類算法，它試圖找到一個超平面來分隔兩個類別的數據點，使得兩側的間隔（margin）最大。

當數據點在高維空間中不是線性可分時，SVM通過使用核函數（kernel function）將原始數據映射到更高維的特征空間，使得數據在新的空間中線性可分。

2.2 原理

SVM的基本原理涉及到高維空間中的數據點和一個決策邊界（也稱為超平面）。它的目標是找到一個超平面，使得不同類別的數據點距離它最遠，這個距離稱為“間隔”。

工作原理如下：

• 數據轉換：首先，SVM將數據點映射到高維空間，這樣它們可以更容易地被一個超平面分開。

• 超平面選擇：然后，SVM嘗試找到一個超平面，使得不同類別的支持向量離它最遠。這個超平面的方程可以表示為：，其中是超平面的法向量，是偏置。

• 間隔最大化：SVM的目標是最大化支持向量到超平面的距離，這個距離稱為“間隔”。間隔的計算公式是：。

• 分類：最后，SVM使用這個超平面來進行分類。對于新的數據點，它會根據這個超平面的位置來決定它屬于哪個類別。

2.3 實現方式

SVM的實現方式主要包括：

• 線性可分SVM：當數據集線性可分時，可以直接使用線性SVM進行分類。

• 線性SVM（軟間隔）：當數據集近似線性可分時，引入松弛變量和懲罰參數，允許部分樣本被錯分。

• 非線性SVM：當數據集非線性可分時，使用核函數將原始數據映射到更高維的特征空間，然后在新的空間中尋找最優超平面。

2.4 算法公式

SVM的公式可能看起來有點嚇人，但我們可以用簡單的例子來解釋它們。

• 數據點的映射：

  • 假設我們在二維空間中有數據點 ((x_1, y_1), (x_2, y_2), \ldots, (x_n, y_n))。
  • 我們可以將它們映射到三維空間，通過增加一個額外的維度 (z)，得到新的數據點 ((x_1, y_1, z_1), (x_2, y_2, z_2), \ldots, (x_n, y_n, z_n))。
  • 這個映射可以通過一個函數 (f) 來實現，例如 (z = f(x, y))。

• 超平面選擇：

  • 在三維空間中，我們的超平面方程可以表示為：[ w_1x + w_2y + w_3z + b = 0 ]。這里的(w_1, w_2, w_3) 是超平面的法向量的分量，(b) 是偏置項。這個超平面將數據點分隔成兩個類別。

• 間隔最大化：

  • 在SVM中，間隔是指數據點到超平面的最短距離。對于任意數據點 ((x, y, z)) 和超平面 (w_1x + w_2y + w_3z + b = 0)，其到超平面的距離 (d) 可以計算為：

    [ d = \frac{|w_1x + w_2y + w_3z + b|}{\sqrt{w_1^2 + w_2^2 + w_3^2}} ]

  • 間隔最大化就是要找到這樣的超平面，使得所有數據點到這個超平面的距離中的最小值最大。

• 分類：

  • 對于新的數據點 ((x_{\text{new}}, y_{\text{new}}, z_{\text{new}}))，我們可以將其映射到三維空間，然后計算它到超平面的距離 (d_{\text{new}})。
  • 根據 (d_{\text{new}}) 的正負以及超平面的位置（由法向量的方向決定），我們可以判斷這個數據點屬于哪一個類別。

2.5 代碼示例

# -*- coding:utf-8 -*-
# @Time   : 2024-02-21
# @Author : Carl_DJ'''
實現功能：用于生成線性可分的數據集并可視化SVM的分界線'''
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.svm import SVC# 生成線性可分的數據集
X, y = datasets.make_classification(n_samples=100, n_features=2, n_informative=2, n_redundant=0, random_state=42)# 創建SVM分類器并擬合數據
clf = SVC(kernel='linear', C=1000)
clf.fit(X, y)# 繪制數據點
plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.Paired, marker='o', edgecolors='k')# 繪制決策邊界
ax = plt.gca()
xlim = ax.get_xlim()
ylim = ax.get_ylim()# 創建網格來評估模型
xx, yy = np.meshgrid(np.linspace(xlim[0], xlim[1], 50), np.linspace(ylim[0], ylim[1], 50))
Z = clf.decision_function(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)# 繪制決策邊界
ax.contour(xx, yy, Z, colors='k', levels=[-1, 0, 1], alpha=0.5, linestyles=['--', '-', '--'])
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.title('SVM Decision Boundary')
plt.show()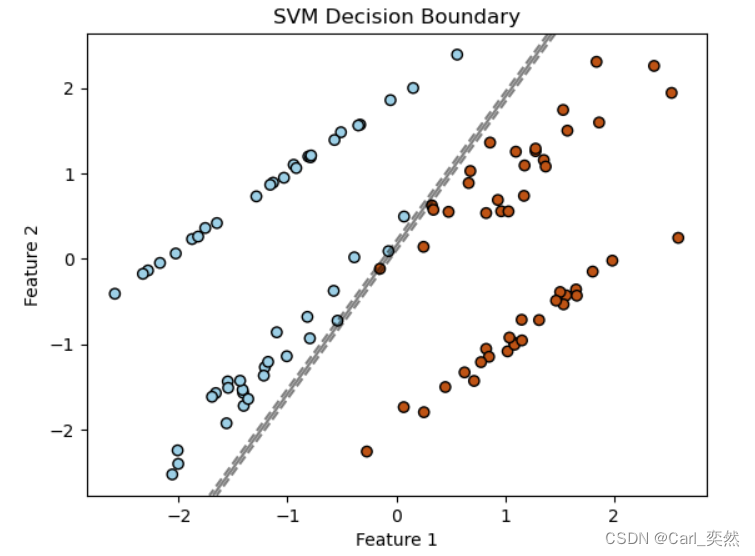

3、總結

支持向量機是一種強大的分類算法，它通過尋找最優超平面來實現分類，并且具有優秀的泛化能力。
SVM對于高維數據的處理效果尤為出色，并且可以通過核函數來處理非線性問題。
然而，SVM的計算復雜度相對較高，尤其是當樣本數量很大時，訓練過程可能會比較慢。
在實際應用中，需要根據具體問題和數據集特點來選擇合適的算法和參數。

我是小魚：

• CSDN 博客專家；
• 阿里云 專家博主；
• 51CTO博客專家；
• 多個名企認證講師等；
• 認證金牌面試官；
• 名企簽約職場面試培訓、職場規劃師；
• 多個國內主流技術社區的認證專家博主；
• 多款主流產品(阿里云等)測評一、二等獎獲得者；

關注小魚，學習機器學習領域的知識。