作為機器學習的基礎算法，SVM被反復提及，西瓜書、wiki都能查到詳細介紹，但是總是覺得還差那么點，于是決定自己總結一下。

一、什么是SVM？

1、解決什么問題？

SVM，最原始的版本是用于最簡單的線性二分類問題。當我們被給了一個新的數據點，其形式是一個p-維的向量，我們想知道它應該屬于被一個（p-1）-維超平面分開的兩半中哪一半。那么我們就想要通過已有數據找到“最有代表性的”超平面。這個超平面就是我們的分類標準。因為我們用到的是超平面而不是曲面，所以這是一個線性的問題。（加入核方法等可以改進為非線性分類）

2、怎么找超平面？?

以下是一個取p=2的示例圖，從圖里可以看出，有許多超平面可以對數據進行分類。（在二維，超平面就是一條直線，需要確定直線的斜率和截距。）最佳超平面的一個合理選擇是代表兩個類別之間最大分離度或邊際的超平面。因此，我們在選擇超平面時，要使它到兩側最近數據點的距離最大。如果存在這樣一個超平面，它就被稱為最大邊際超平面（maximum-margin hyperplane），而它所定義的線性分類器就被稱為最大邊際分類器（maximum-margin classifier）；或者等同于最佳穩定性感知器（the perceptron of optimal stability）。【from wiki】

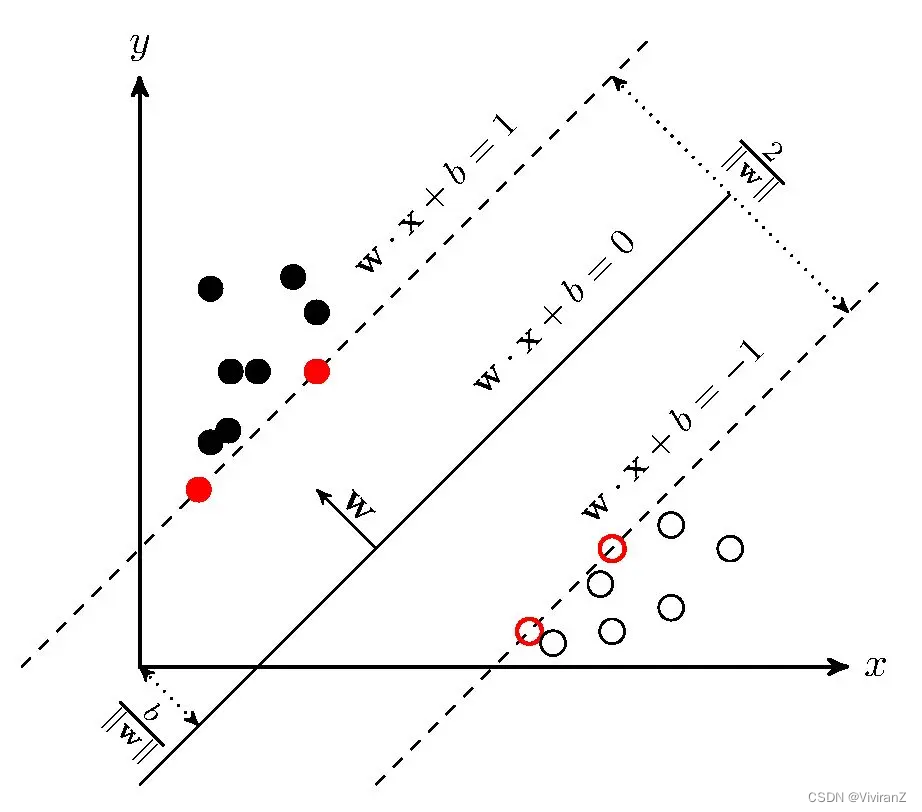
3、如何定義“最大距離”？

這一步博客?

支持向量機（SVM）——原理篇

里講的很清晰了，基本也和西瓜書一致，我就不加贅述，簡而言之，就是設出超平面的參數方程，代入求距離最近的點（min），再調整參數方程讓最近的點距離盡量遠（max）。

這種二次規劃問題，一眼要用到拉格朗日乘子法求對偶問題，都是很基礎的優化方法。

最終得到：

4、為什么叫“支持向量機”？

接下來這段話很簡單但是清晰說明了SVM的本質：

?也就是說，最終我們只會考慮支持向量。

定義：距離超平面最近的幾個訓練樣本點使得，這幾個樣本（由向量表示）被稱為支持向量。兩個異類支持向量到超平面的距離之和為，被稱為間隔（margin）。

5、總結

SM，就是把分類問題或者回歸問題，轉化為基于已知的分類點求一個分類效果最好的分割超平面，進而可以用優化方法求解。

二、一些特殊的優化技巧？?

1、核方法

a. 解決什么問題？

?基礎的SVM需要假設所有樣本是線性可分的，但是實際任務可能不是，而是需要一個曲面。

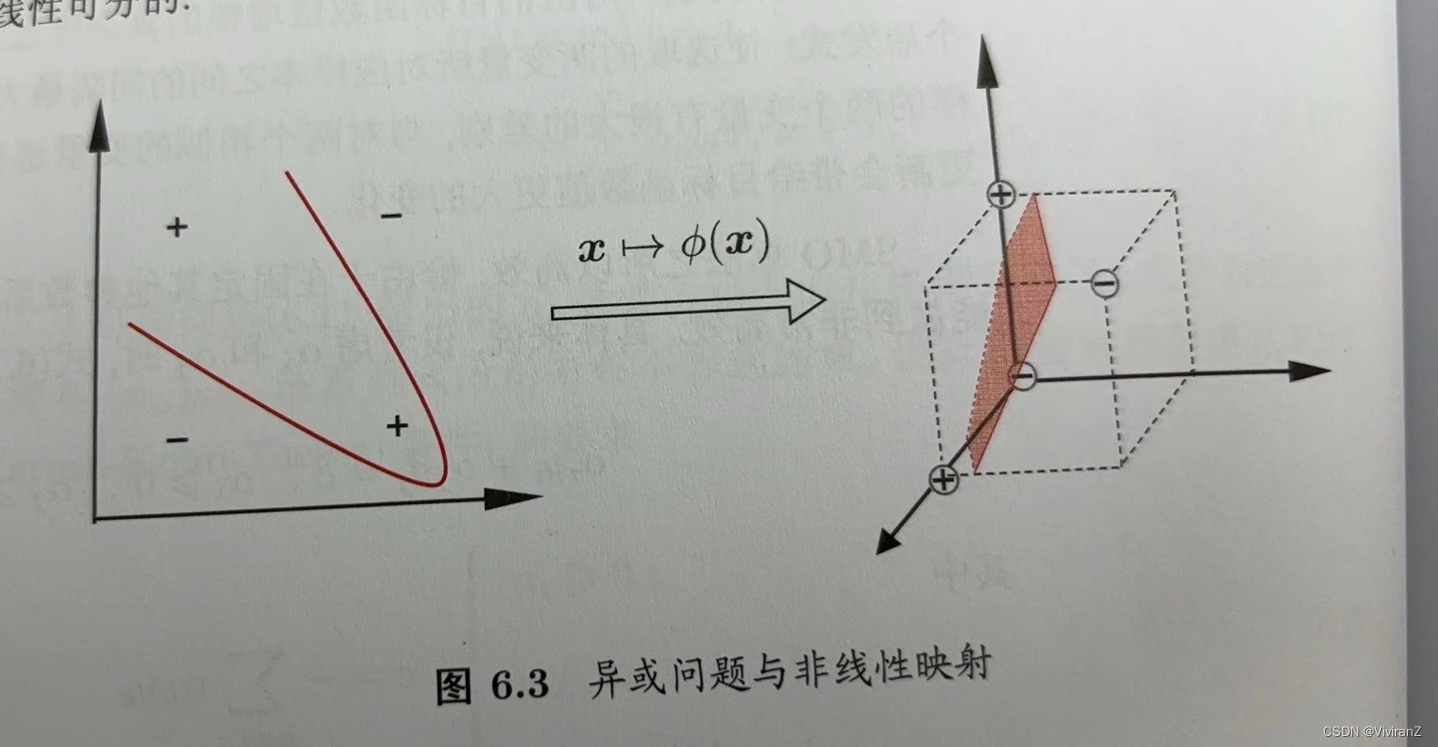
對這樣的問題，可將樣本從原始空間映射到一個更高維的特征空間，使得樣本在這個特征空間內線性可分：例如在圖6.3中，若將原始的二維空間映射到一個合適的三維空間，就能找到一個合適的劃分超平面，幸運的是，如果原始空間是有限維，即屬性數有限，那么一定存在一個高維特征空間使樣本可分。【引自西瓜書】

b.如何實現？

簡單來說，就是找一個映射，把原本的數據映射到，通過推演我們發現

具體實現細節可以參考西瓜書或者以下博客：?
j??????????????淺入淺出核方法 (Kernel Method) - 知乎

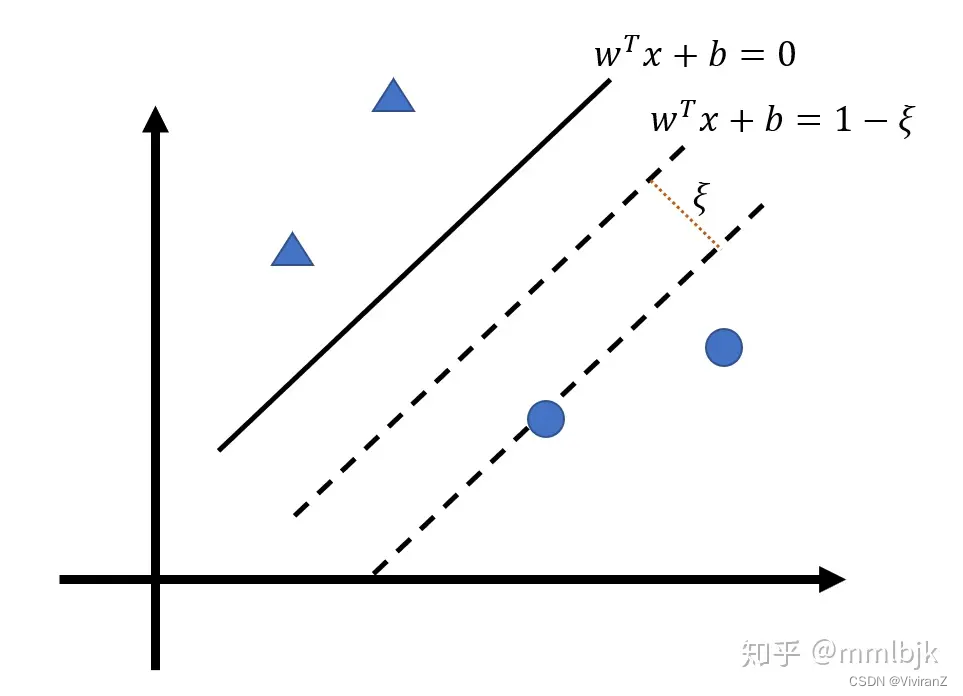
2、軟間隔

a. 解決什么問題？

即使我們用了核方法讓原本不是線性可分的數據變得貌似線性可分，我們也不知道是不是過擬合了，緩解方法之一就是允許算法在一些樣本上出錯、也就是把硬間隔變成軟間隔。

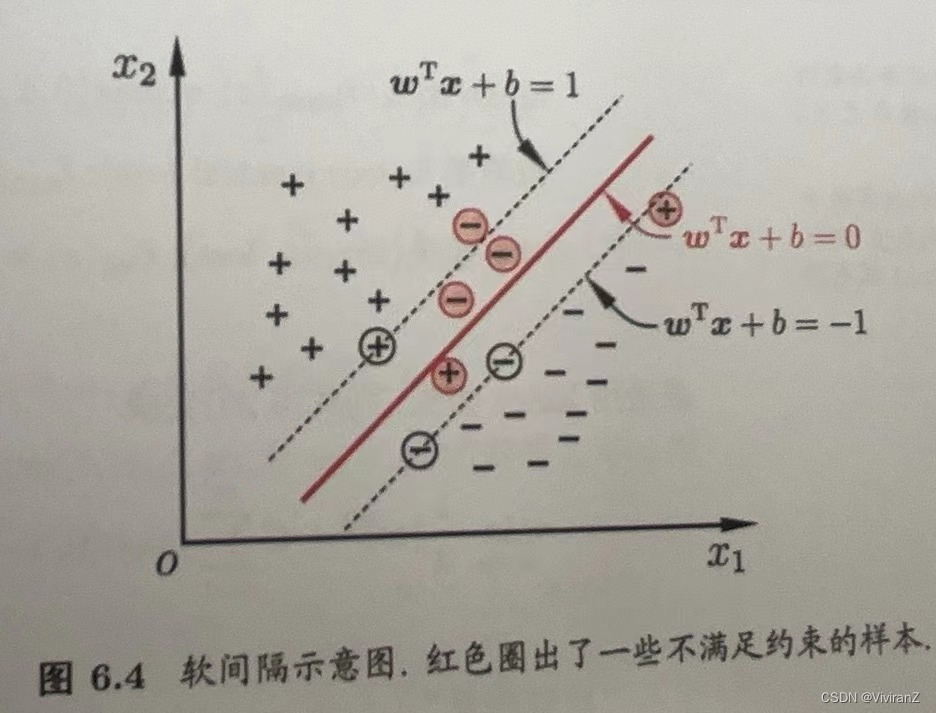
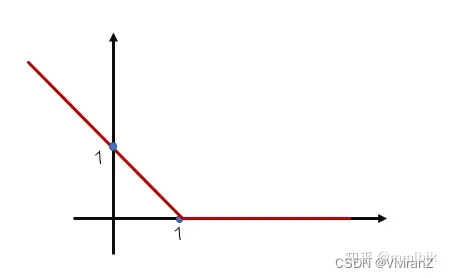
那么問題就變成如何讓不滿足約束的樣本盡量少。?

線性SVM之硬間隔和軟間隔的直覺和原理 - 知乎

這個講得還挺清晰的。。。????????

?

三、支持向量回歸

回歸問題和分類問題不同，分類是希望樣本盡量遠離預測的超平面，而回歸是希望樣本盡量靠近預測的超平面。一般來說就是落入間隔帶。?

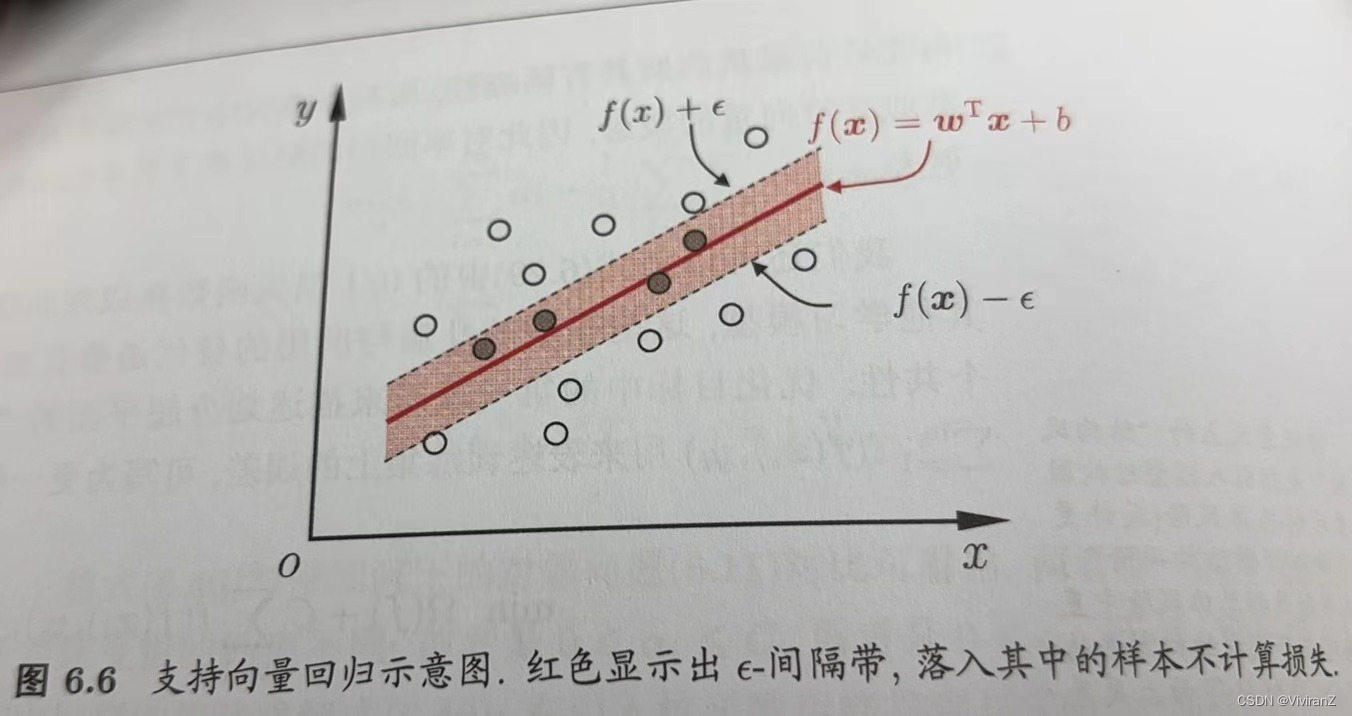
細節不表。可參考西瓜書。

參考文獻：

[1]?https://en.wikipedia.org/wiki/Support_vector_machine

[2]《機器學習》周志華

[3]支持向量機（SVM）——原理篇

[4]淺入淺出核方法 (Kernel Method) - 知乎?

[5]?線性SVM之硬間隔和軟間隔的直覺和原理 - 知乎