在開始講述SVM算法之前，我們先來看一段定義：

'''
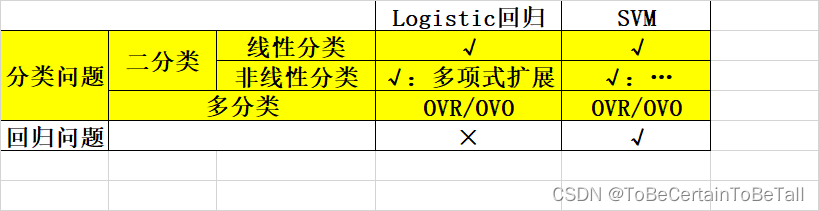
支持向量機(Support VecorMachine, SVM)本身是一個二元分類算法，支持線性分類和非線性分類的分類應用，同時通過OvR或者OvO的方式可以應用在多元分類領域中能夠直接將SVM應用于回歸應用中
在不考慮集成學習算法或者特定的數據集時，SVM在分類算法中可以說是一種特別優秀的算法
'''

一. SVM的優越性

在Logistic回歸算法中：
????我們追求是尋找一條決策邊界，即找到一條能夠正確劃分所有訓練樣本的邊界；
????當所有樣本正確劃分時，損失函數已降至最低，模型不再優化

在SVM算法中：
????我們追求是尋找一條最優決策邊界

	那什么是最優呢？SVM提出的基本思想是，尋找一條決策邊界，使得該邊界到兩邊最近的點間隔最大這樣做得目的在于：相比于其他邊界，svm尋找到的邊界對于樣本的局部擾動容忍性最好，對新進樣本更容易判斷正確；也就是說，此時決策邊界具有最好的魯棒性

二. SVM算法推導

	注意：下面講述的是線性分類

這里我們換一種思路尋找最佳決策邊界：

首先假設決策邊界為
$$y=\overrightarrow{\omega }?\overrightarrow{x}+b$$

公式解釋1：
?
為什么要這么設方程呢？

我們希望通過向量點乘來確定距離
換句話說，希望通過向量點乘來確定正負樣本的邊界

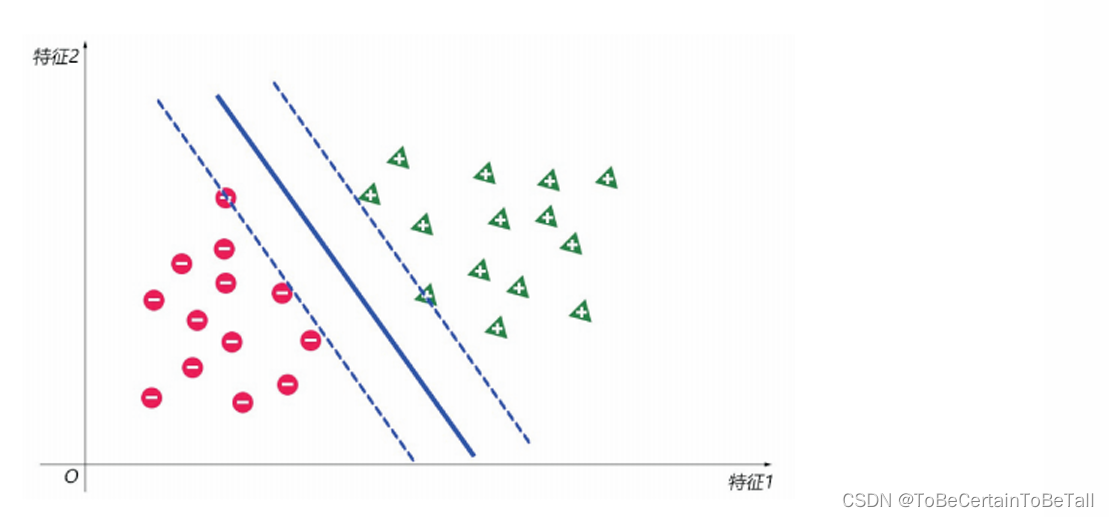
為了尋找最佳決策邊界，我們可以：
以上述決策邊界為中心線，向兩邊做平行線，讓這兩條平行線過兩邊最近的樣本點；此時會形成一條“街道”，最佳決策邊界就是使這條街道最寬的那個決策邊界。

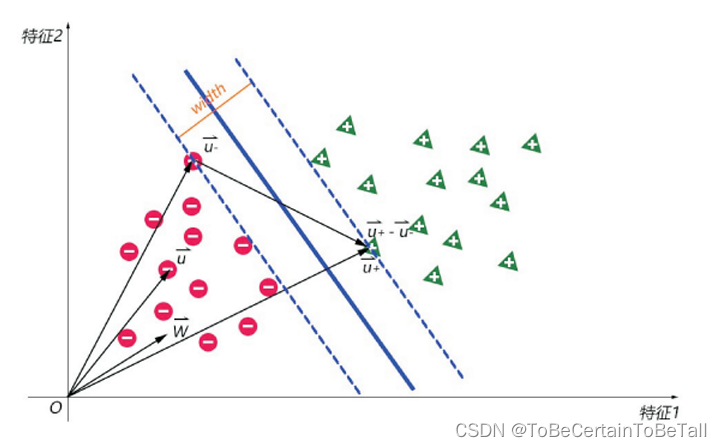
補充一點：
在Logistic回歸算法中，我們人為的將數據集設為1，0
在SVM算法中，我們人為的將數據集設為1，-1
?
參數說明：

width：街寬
?
$\overrightarrow{\omega }$：決策邊界的法向量
?
$\overrightarrow{u_{?}}$：街邊上的負樣本向量
?
$\overrightarrow{u_{+}}$：街邊上的正樣本向量
?
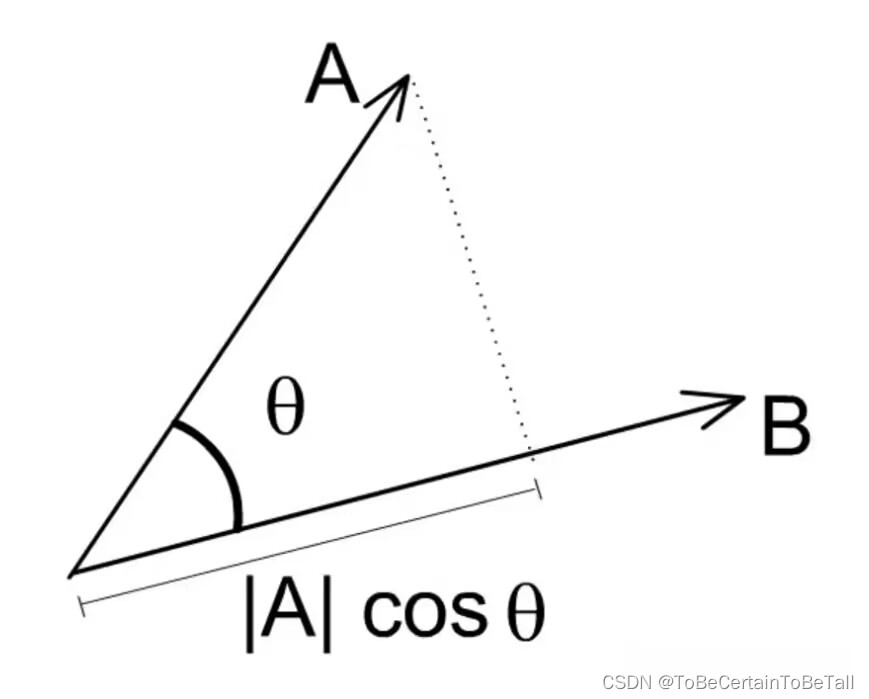
單位向量：$\frac{\overrightarrow{a}}{\Vert a\Vert }$

向量點乘幾何的意義：
$\overrightarrow{a}?\overrightarrow{b}=\left|\overrightarrow{a}\right||\overrightarrow{b}|\cos \theta$
可以理解為$\overrightarrow{a}$ 在$\overrightarrow{b}$上的投影長度乘以$|\overrightarrow{b}|$的模長

對于訓練集中的任何一個數據，我們總會取到一個合適長度的$\overrightarrow{\omega }$，以及一個適合的常數b，得到：
$$\{\begin{array}{c}\overrightarrow{\omega }?\overrightarrow{u_{+}}+b\ge 1\\ \overrightarrow{\omega }?\overrightarrow{u_{?}}+b\le ?1\end{array}$$

即可以合并為：$$y_i(\overrightarrow{\omega }?\overrightarrow{u_i}+b)\ge 1$$
而對于街邊點而言，滿足
$$y_i(\overrightarrow{\omega }?\overrightarrow{u_i}+b)=1$$

	注意：這些街邊點對于決定決策邊界取決定性作用，因此被稱為支持向量

---

這樣，我們就可以用數學方式將上述街寬抽象出來：
$$width=(\overrightarrow{u_{+}}?\overrightarrow{u_{?}})?\frac{\overrightarrow{w}}{\Vert w\Vert }$$
推導式子，就可以進一步得到：

$width=(\overrightarrow{u_{+}}?\overrightarrow{u_{?}})?\frac{\overrightarrow{w}}{\Vert w\Vert }$

???????$=\frac{\overrightarrow{u_{+}}?\overrightarrow{{\omega }_{}}}{\Vert \overrightarrow{\omega }\Vert }?\frac{\overrightarrow{u_{?}}?\overrightarrow{{\omega }_{}}}{\Vert \overrightarrow{\omega }\Vert }$

???????$=\frac{1?b}{\Vert \overrightarrow{w}\Vert }?\frac{?1?b}{\Vert \overrightarrow{w}\Vert }$

???????$=\frac{2}{\Vert \overrightarrow{w}\Vert }$

此時，我們要求街寬最大，即是求$min(\Vert \overrightarrow{w}\Vert )$，這里為了后續求導方便，將值寫成$min(\frac{1}{2}{\Vert \overrightarrow{w}\Vert }^2)$

需要明確，"街邊"最大值的條件是基于支持向量的，而支持向量是屬于數據集的，因此我們的問題就變成了：
$$\{\begin{array}{c}min(\frac{1}{2}{\Vert \overrightarrow{w}\Vert }^2)\\ s.t.y_i(\overrightarrow{\omega }?\overrightarrow{x}+b)?1\ge 0\end{array}$$

這是一個典型的條件極值問題，我們用拉格朗日乘數法，得到拉格朗日函數為：
$$L=\frac{1}{2}{\Vert \overrightarrow{w}\Vert }^2?\sum _{i=1}^m{\beta }_i[y_i(\overrightarrow{\omega }?\overrightarrow{x}+b)?1],({\beta }_i\ge 0)$$

這里的約束是不等式約束，所以要使用KKT條件(KKT是拉格朗日乘數法的一種泛化形式，此時${\beta }_i\ge 0$)，而KKT條件的計算方式為：$$\underset{\beta \ge 0}{\max }\underset{w,b}{\min }L(w,b,\beta )$$

$$\frac{?L}{?w}=w?\sum _{i=1}^m{\beta }_i{x}^{(i)}{y}^{(i)}=0?w=\sum _{i=1}^m{\beta }_i{x}^{(i)}{y}^{(i)}$$

$$\frac{?L}{?b}=?\sum _{i=1}^m{\beta }_i{y}^{(i)}=0?0=\sum _{i=1}^m{\beta }_i{y}^{(i)}$$

公式解釋：
$\beta$是每個樣本對應的拉格朗日乘子

對于非支持向量而言， $\beta =0$，即對非支持向量無約束

則：$y^{(i)}?0=0$

對于支持向量而言， $\beta >0$，即對支持向量有約束

則：$正樣本支持向量?1+負樣本支持向量?(?1)=0$

此時$L(\beta )$為：

$L(\beta )=\frac{1}{2}{\Vert \overrightarrow{w}\Vert }^2?{\sum }_{i=1}^m{\beta }_i[y^{(i)}({\omega }^T?x^{(i)}+b)?1]$

????? $=\frac{1}{2}{\omega }^T\omega ?{\sum }_{i=1}^m{\beta }_i{y}^{(i)}{\omega }^T?x^{(i)}?b{\sum }_{i=1}^m{\beta }_i{y}^{(i)}+{\sum }_{i=1}^m{\beta }_i$

????? $=\frac{1}{2}{\omega }^T{\sum }_{i=1}^m{\beta }_i{x}^{(i)}{y}^{(i)}?{\sum }_{i=1}^m{\beta }_i{y}^{(i)}{\omega }^T{x}^{(i)}+{\sum }_{i=1}^m{\beta }_i$

????? $=?\frac{1}{2}{\omega }^T{\sum }_{i=1}^m{\beta }_i{x}^{(i)}{y}^{(i)}+{\sum }_{i=1}^m{\beta }_i$

????? $=?\frac{1}{2}({\sum }_{j=1}^m{\beta }_j{x}^{(j)}{y}^{(j)}{)}^T({\sum }_{i=1}^m{\beta }_i{x}^{(i)}{y}^{(i)})+{\sum }_{i=1}^m{\beta }_i$

????? $=?\frac{1}{2}{\sum }_{j=1}^m{\beta }_j{x}^{(j{)}^T}{y}^{(j)}{\sum }_{i=1}^m{\beta }_i{x}^{(i)}{y}^{(i)}+{\sum }_{i=1}^m{\beta }_i$

????? $={\sum }_{i=1}^m{\beta }_i?\frac{1}{2}{\sum }_{i=1}^m{\sum }_{j=1}^m{\beta }_i{\beta }_j{y}^{(i)}{y}^{(j)}{x}^{(j{)}^T}{x}^{(i)}$

即：$$\{\begin{array}{c}L(\beta )={\sum }_{i=1}^m{\beta }_i?\frac{1}{2}{\sum }_{i=1}^m{\sum }_{j=1}^m{\beta }_i{\beta }_j{y}^{(i)}{y}^{(j)}{x}^{(j{)}^T}{x}^{(i)}\\ s.t:{\sum }_{i=1}^m{\beta }_i{y}^{(i)}=0\end{array}$$

解到這一步，我們發現L函數只與$\beta$有關，所以此時可以直接極大化我們的優化函數，且
$$\underset{\beta \ge 0}{\max }l(\beta )?\underset{\beta \ge 0}{\min }?l(\beta )$$
因此，求解$\beta$就變成了
$$\{\begin{array}{c}{\min }_{\beta \ge 0}\frac{1}{2}{\sum }_{i=1}^m{\sum }_{j=1}^m{\beta }_i{\beta }_j{y}^{(i)}{y}^{(j)}{x}^{(j{)}^T}{x}^{(i)}?{\sum }_{i=1}^m{\beta }_i\\ s.t:{\sum }_{i=1}^m{\beta }_i{y}^{(i)}=0\end{array}$$

但是對于$\beta$，可以使用SMO算法求得；對于SMO算法，我們先放一放

這里，假設我們用SMO求得了$\beta$的最優解，那么我們可以分別計算得到對應的：

$w={\sum }_{i=1}^m{\beta }_i{x}^{(i)}{y}^{(i)}$
b：一般使用所有支持向量的計算均值作為實際值

怎么得到支持向量呢？
$\beta =0$，該樣本不是支持向量
$\beta >1$，該樣本是支持向量

小節

對于線性可分的m個樣本(x1,y1)，(x2,y2)… ：

	x為n維的特征向量y為二元輸出，即+1，-1

SVM輸出的為w，b，分類決策函數

通過構造約束問題：
$$\{\begin{array}{c}{\min }_{\beta \ge 0}\frac{1}{2}{\sum }_{i=1}^m{\sum }_{j=1}^m{\beta }_i{\beta }_j{y}^{(i)}{y}^{(j)}{x}^{(j{)}^T}{x}^{(i)}?{\sum }_{i=1}^m{\beta }_i\\ s.t:{\sum }_{i=1}^m{\beta }_i{y}^{(i)}=0\end{array}$$
使用SMO算法求出上述最優解$\beta$
找到所有支持向量集合：
$$S=(x^{(i)},y^{(i)})(\beta >0,i=1,2,...,m)$$
從而更新w，b

$w={\sum }_{i=1}^m{\beta }_i{x}^{(i)}{y}^{(i)}$

$b=\frac{1}{S}{\sum }_{i=1}^S(y^s?{\sum }_{i=1}^m{\beta }_i{x}^{(i{)}^T}{y}^{(i)}{x}^s)$

構造最終的分類器，為：
$$f(x)=sign(w?x+b)$$

	x<0時，y=-1x=0時，y=0x>0時，y=1注意：假設，不會出現0若出現，正負樣本隨意輸出一個，即+0.00000001或-0.00000001都可以

概念

最后，我們定義具體概念：

分割超平面(Separating Hyperplane)：將數據集分割開來的直線、平面叫分割超平面

支持向量(Support Vector)：離分割超平面最近的那些點叫做支持向量

間隔(Margin)：支持向量數據點到分割超平面的距離稱為間隔；任何一個支持向量到分割超平面的距離都是相等的

---

感謝閱讀🌼
如果喜歡這篇文章，記得點贊👍和轉發🔄哦！
有任何想法或問題，歡迎留言交流💬，我們下次見！
本文相關代碼存放位置
????

祝愉快🌟！

---