輪廓系數(Silhouette Coefficient)是評估聚類算法效果的常用指標之一。它結合了聚類的凝聚度(Cohesion)和分離度(Separation),能夠量化聚類結果的緊密度和分離度。
背景
1.聚類分析的背景
在數據挖掘和機器學習領域,聚類分析是一種常用的無監督學習方法,用于將數據集中的對象劃分為具有相似特征的簇。聚類分析的目標是發現數據中的內在結構,將相似的數據點歸為一類,并使不同類別之間的差異最大化。通過聚類,我們可以識別出數據中的模式、群集和關聯,從而進行進一步的分析和決策制定。
2.評估聚類效果的需求
在進行聚類分析時,評估聚類效果是至關重要的。一個好的聚類結果應該具有以下特征:
簇內的樣本應該盡可能相似。
不同簇之間應該盡可能不相似。
因此,我們需要一種評估指標來衡量聚類的緊密度和分離度,以便對不同的聚類結果進行比較,并選擇最佳的聚類數目和算法。
3.輪廓系數的產生
輪廓系數是由Peter J. Rousseeuw 在1987年提出的。它的提出是為了克服傳統的聚類評估方法的局限性,如僅僅依賴于簇內的均方差來評估聚類效果。輪廓系數的目的是同時考慮簇內和簇間的距離,從而提供更全面的聚類質量評估。輪廓系數是一種相對直觀且易于理解的指標,它將聚類的緊密度和分離度結合在一起,提供了對聚類質量的綜合評價。它的取值范圍在-1到1之間,值越接近1表示聚類效果越好,值越接近-1表示聚類效果越差。
定義
輪廓系數通過計算每個數據點的輪廓系數來評估聚類的質量。輪廓系數的計算基于以下兩個因素:
-
簇內相似度(凝聚度)(a):數據點與同一簇內其他點的平均距離。它衡量了數據點與其所屬簇的緊密程度。
-
簇間不相似度(分離度)(b):數據點與其最近的不同簇的所有點的平均距離。它衡量了數據點與其他簇的分離程度。
計算過程
對于每個數據點i,其輪廓系數 s i s_i si??可以通過以下公式計算:
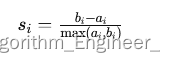
其中,
a i a_i ai?? 是數據點i與其所屬簇內其他點的平均距離。
b i b_i bi?? 是數據點i與最近的不同簇中所有點的平均距離。
對于整個數據集,輪廓系數SS是所有數據點的輪廓系數的平均值。
解釋
輪廓系數的取值范圍在-1到1之間。
當輪廓系數接近1時,表示簇內相似度高,簇間不相似度低,聚類效果好。
當輪廓系數接近0時,表示簇內相似度和簇間不相似度相當,聚類效果一般。
當輪廓系數接近-1時,表示簇內相似度低,簇間不相似度高,聚類效果差。
優缺點
優點:能夠同時考慮簇內和簇間的距離,提供了對聚類質量的全面評估。易于理解和計算,適用于各種類型的聚類算法。缺點:對聚類形狀和密度不敏感,可能無法有效地處理非凸形狀的簇或密度不均勻的簇。受到數據集不均衡的影響,可能導致評估結果不準確。
應用
輪廓系數廣泛應用于各種聚類算法的性能評估和比較,如K均值聚類、層次聚類、DBSCAN等。它也被用于確定最佳的聚類數目和幫助解釋聚類結果。



)
)


邏輯回歸與交叉熵--九五小龐)








)


