2023年第十四屆藍橋杯大賽軟件類省賽C/C++大學A組部分真題和題解分享

藍橋杯2023年第十四屆省賽真題-平方差

題目描述
給定 L, R，問 L ≤ x ≤ R 中有多少個數 x 滿足存在整數 y,z 使得 x = y2 ? z2。
輸入格式
輸入一行包含兩個整數 L, R，用一個空格分隔。
輸出格式
輸出一行包含一個整數滿足題目給定條件的 x 的數量。
樣例輸入
1 5
樣例輸出
4
提示
1 = 12 ? 02 ；
3 = 22 ? 12 ；
4 = 22 ? 02 ；
5 = 32 ? 22 。
對于 40% 的評測用例，LR ≤ 5000 ；
對于所有評測用例，1 ≤ L ≤ R ≤ 109 。

思路題解

解題思路:

• 規律：只有當x為奇數或4的倍數時才能拆分為兩個數的平方差。
  注意事項:
• 剛開始用c++寫循環的時候，有一個樣例會超時，故進一步尋找規律：F(X)=x/4+(x+1)/2，該式代表不大于x的滿足條件的數的個數，用F?-F(L-1)即為L-R之間（大于等于L，小于等于R）滿足條件的數的個數。

#include<iostream>
using namespace std;
int F(int x) {return x / 4 + (x + 1) / 2;//不大于x的滿足條件的數的個數
}
int main() {int l = 0, r = 0;cin >> l >> r;cout << F(r)-F(l-1);return 0;
}

藍橋杯2023年第十四屆省賽真題-更小的數

題目描述

輸入格式
輸入一行包含一個長度為 n 的字符串表示 num（僅包含數字字符 0 ～ 9），
從左至右下標依次為 0 ～ n ? 1。
輸出格式
輸出一行包含一個整數表示答案。
樣例輸入
210102
樣例輸出
8
提示
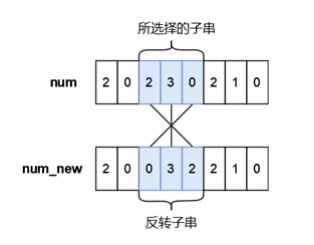
一共有 8 種不同的方案：
1）所選擇的子串下標為 0 ～ 1 ，反轉后的 numnew = 120102 < 210102 ；
2）所選擇的子串下標為 0 ～ 2 ，反轉后的 numnew = 012102 < 210102 ；
3）所選擇的子串下標為 0 ～ 3 ，反轉后的 numnew = 101202 < 210102 ；
4）所選擇的子串下標為 0 ～ 4 ，反轉后的 numnew = 010122 < 210102 ；
5）所選擇的子串下標為 0 ～ 5 ，反轉后的 numnew = 201012 < 210102 ；
6）所選擇的子串下標為 1 ～ 2 ，反轉后的 numnew = 201102 < 210102 ；
7）所選擇的子串下標為 1 ～ 4 ，反轉后的 numnew = 201012 < 210102 ；
8）所選擇的子串下標為 3 ～ 4 ，反轉后的 numnew = 210012 < 210102 ；

對于 20% 的評測用例，1 ≤ n ≤ 100 ；
對于 40% 的評測用例，1 ≤ n ≤ 1000 ；
對于所有評測用例，1 ≤ n ≤ 5000 。

思路題解

解題思路:

中心思想：s[l] > s[r]則滿足條件，答案的個數+1。

詳細解釋：考慮s的所有子串[l,r], l即left，是子串的起始下標，r即right是子串的末尾下標，判斷s[l] 和 s[r]的大小關系:

• 若s[l] > s[r]則該子串反轉后，新串<原串，滿足條件，答案數+1；

• 若s[l] = s[r]則將子串區間[l,r]縮小為[l+1,r-1],再判斷s[l+1]和s[r-1]的大小關系；

• 若s[l] < s[r]則該子串反轉后，新串>原串，不滿足條件。

注意事項:

• 注意l和r的取值范圍（詳見代碼注釋）。

#include<iostream>
#include<string>
using namespace std;
string s;
int F(int l, int r) {while (l < r) {if (s[l] > s[r])return 1;//如果s[l] > s[r]，反轉后滿足條件 新字符串<原字符串。else if (s[l] == s[r]) { l++;r--; }//如果s[l] == s[r]，兩邊同時縮小區間。else break;//如果s[l] < s[r]，不用繼續考慮，反轉后一定不滿足條件，直接退出循環}return 0;
}
int main(){cin >> s;int n = s.length();//n是字符串長度int ans = 0;//記錄答案for (int l = 0;l <= n - 2;l++) {//l即left是子串的起始下標，從0開始到n-2（子串長度至少為2，最右側的最小子串下標為[n-2,n-1],故l最多到n-2）for (int r = n - 1;r > l;r--) {//r即right是子串的末尾下標，從s的最末下標n-1到l+1。if(F(l,r))ans++;}}cout << ans;return 0;
}

藍橋杯2023年第十四屆省賽真題-顏色平衡樹

題目描述
給定一棵樹，結點由 1 至 n 編號，其中結點 1 是樹根。樹的每個點有一個顏色 Ci。
如果一棵樹中存在的每種顏色的結點個數都相同，則我們稱它是一棵顏色平衡樹。
求出這棵樹中有多少個子樹是顏色平衡樹。
輸入格式
輸入的第一行包含一個整數 n ，表示樹的結點數。
接下來 n 行，每行包含兩個整數 Ci , Fi，用一個空格分隔，表示第 i 個結點的顏色和父親結點編號。
特別地，輸入數據保證 F1 為 0 ，也即 1 號點沒有父親結點。保證輸入數據是一棵樹。
輸出格式
輸出一行包含一個整數表示答案。
樣例輸入
6
2 0
2 1
1 2
3 3
3 4
1 4
樣例輸出
4
提示
編號為 1, 3, 5, 6 的 4 個結點對應的子樹為顏色平衡樹。
對于 30% 的評測用例，n ≤ 200，Ci ≤ 200 ；
對于 60% 的評測用例，n ≤ 5000，Ci ≤ 5000 ；
對于所有評測用例，1 ≤ n ≤ 200000，1 ≤ Ci ≤ 200000，0 ≤ Fi < i 。

思路題解

思路：

• 要判斷每個子樹是否為平衡樹，需要統計子樹的每種顏色的節點的數量，并判斷所有數量是否相等。

• 對于一顆樹的根節點，若該樹的所有子樹的統計結果都得到了，就可以直接將子樹的統計結果累加，并加上根節點的顏色。因此可以使用dfs對樹進行搜索，在后序遍歷位置得到子樹的統計結果并累加，就可以計算出該樹的統計結果，判斷所有顏色數量是否相等即可。

注意：

• 統計結果cnt使用數組時，需要判斷整顆樹所有顏色的數量，而部分子樹的顏色并不包含所有的顏色，每次判斷的時間復雜度為O(num_c)，num_c為整棵樹的顏色種數，這樣會超時。因此可以使用map數據結構，這樣每次只需判斷子樹所包含的顏色。

#include<iostream>
#include<vector>
#include<cstring>
#include<map>
using namespace std;
const int N = 2e5+1;
//最終結果
int ans=0;
//將子樹的計數結果cnt_nb累加到根節點的結果cnt上
void add(map<int,int>& cnt,map<int,int>& cnt_nb){for(auto entry:cnt_nb){int c=entry.first,count = entry.second;cnt[c] += count;}
}
/*
對樹進行dfs搜索，樹的根節點為i，并返回該子樹的各節點顏色計數結果
*/
map<int,int> dfs(vector<int>* g,int* c,int i){int sz = g[i].size();map<int,int> cnt; //記錄子樹的每個節點的各顏色節點的數量/*如果為葉子節點，直接返回*/if(sz==0){ cnt[c[i]] = 1; ans++; return cnt;}/*如果不是葉子節點*///將根節點的顏色加入cntcnt[c[i]]=1;//遍歷根節點的所有子樹，并將子樹的計數結果累加到cnt中for(int j=0;j<sz;j++){int nb = g[i][j];map<int,int> cnt_nb = dfs(g,c,nb);add(cnt,cnt_nb);} //判斷該子樹的各種顏色節點的數量是否相等int count = cnt[c[i]];for(auto entry:cnt){//存在一種顏色數量不等，直接返回if(entry.second != count) return cnt; }//各顏色的數量相等，結果+1ans++;//返回計數結果return cnt;
}
int main()
{int n;cin>>n;vector<int> g[N]; int c[N]; //每個節點的顏色for(int i=0;i<n;i++){int f;cin>>c[i]>>f;if(f>=1){g[f-1].push_back(i); //記錄節點f的子節點i（節點編號從0開始）}}dfs(g,c,0);cout<<ans;return 0;
}

藍橋杯2023年第十四屆省賽真題-買瓜

題目描述
小藍正在一個瓜攤上買瓜。瓜攤上共有 n 個瓜，每個瓜的重量為 Ai 。
小藍刀功了得，他可以把任何瓜劈成完全等重的兩份，不過每個瓜只能劈一刀。
小藍希望買到的瓜的重量的和恰好為 m 。
請問小藍至少要劈多少個瓜才能買到重量恰好為 m 的瓜。如果無論怎樣小藍都無法得到總重恰好為 m 的瓜，請輸出 ?1 。
輸入格式
輸入的第一行包含兩個整數 n, m，用一個空格分隔，分別表示瓜的個數和小藍想買到的瓜的總重量。
第二行包含 n 個整數 Ai，相鄰整數之間使用一個空格分隔，分別表示每個瓜的重量。
輸出格式
輸出一行包含一個整數表示答案。
樣例輸入
3 10
1 3 13
樣例輸出
2
提示
對于 20% 的評測用例，∑n≤10；
對于 60% 的評測用例，∑n≤20；
對于所有評測用例，1 ≤n≤30，1≤ Ai ≤ 109 ，1 ≤ m ≤ 109

思路題解

對于每一個瓜有三種選擇:
1)買整個瓜
2)買半個瓜，需要增加劈瓜次數
3)不買

則可以使用深度優先搜索解決, 對每個瓜的三種選擇進行搜索, 解空間樹是一顆完全三叉樹, 時間復雜度為O(3^n), 肯定會超時, 故需要進行剪枝。

買半個瓜時需要將重量除2，會產生小數，故可以將重量數組都乘2，最大重量也乘2。

搜索時需要記錄三個狀態，當前層數pos，當前總重量sum，當前劈瓜的次數cnt，以下情況需要剪枝：
1）當前劈瓜次數大于已求得的最小次數，即cnt>ans
2）當前重量之和大于要求的重量，即sum>m

但是這樣仍然會超時，還可以將重量數組降序排列，使得更快剪枝。還可以創建一個重量數組的后綴數組suf，這樣在搜索時可以利用其剪枝：若當前重量加上剩余的所有瓜重量之和小于要求的重量，剪枝。

#include<iostream>
#include<algorithm>
using namespace std;
const int N = 30; 
int INF = 100;
int n,m;
int v[N]; //重量數組
long suf[N+1]; //重量數組的后綴數組
int ans = INF; //將結果初始化為INF
/*
dfs搜索,參數分別表示當前層數,當前重量之和,切瓜的次數
*/
void dfs(int pos,long sum,int cnt){if(sum==m){ //找到了一個結果ans = min(ans,cnt);return;}//剪枝if(pos>=n || cnt>=ans || sum>m || sum+suf[pos]<m) return;//對三種選擇進行搜索dfs(pos+1,sum+v[pos],cnt); dfs(pos+1,sum+v[pos]/2,cnt+1);dfs(pos+1,sum,cnt);
}
int main()
{ios::sync_with_stdio(false);cin.tie(0),cout.tie(0);cin>>n>>m;m*=2; //總重量乘2for(int i=0;i<n;i++) cin>>v[i],v[i]*=2;sort(v,v+n,greater<int>());for(int i=n-1;i>=0;i--) suf[i] = suf[i+1]+v[i];dfs(0,0,0);if(ans==INF) cout<<-1;else cout<<ans;return 0;
}