1.圖論基礎概念
概念
(注意連通非連通情況,+1節點)
無向圖: 度是邊的兩倍(沒有入度和出度的概念)
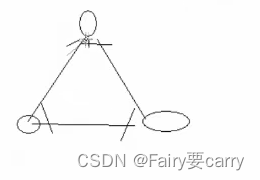
1.完全圖: 假設一個圖有n個節點,那么任意兩個節點都有邊則為完全圖
2.連通圖:是指任意兩個結點之間都有一個路徑相連。
3.區別: n個頂點的完全圖有n(n-1)/2條邊;而連通圖則不一定,但至少有n-1條邊。舉個例子,四個頂點的完全圖有6條邊,也就是四條邊加上2條對角線;而連通圖可以只包含周圍四條邊就可以了。
4.強連通圖:
你到我有路徑,我到你有路徑——>最少邊數為n(環),至多邊數為n(n-1);
有向圖G中,如果兩個頂點vi,vj間(vi>vj)有一條從vi到vj的有向路徑,同時還有一條從vj到vi的有向路徑,則稱兩個頂點強連通(strongly connected)。如果有向圖G的每兩個頂點都強連通,稱G是一個強連通圖。
5.連通分量:
- 子圖相通
- 子圖極大
與連通圖對應,一般書上說的都是特指無向圖!!
首先要知道分量,分量其實就是子圖,只不過說的高大尚罷了。但連通分量不是簡單的子圖連通,他還除了要求子圖連通,還要求該連通子圖極大。說白了,無向圖極大連通子圖就是連通分量。到這里先往下看極大連通子圖再回來看

6.極大連通分量:
從5我們知道他首先是連通子圖,并且該連通子圖是極大的,主要是這里的極大很不好理解。這里我畫圖舉例

7.極小連通分量:

7.生成樹:
連通圖的生成樹是包含圖中全部頂點的一個極小連通子圖。

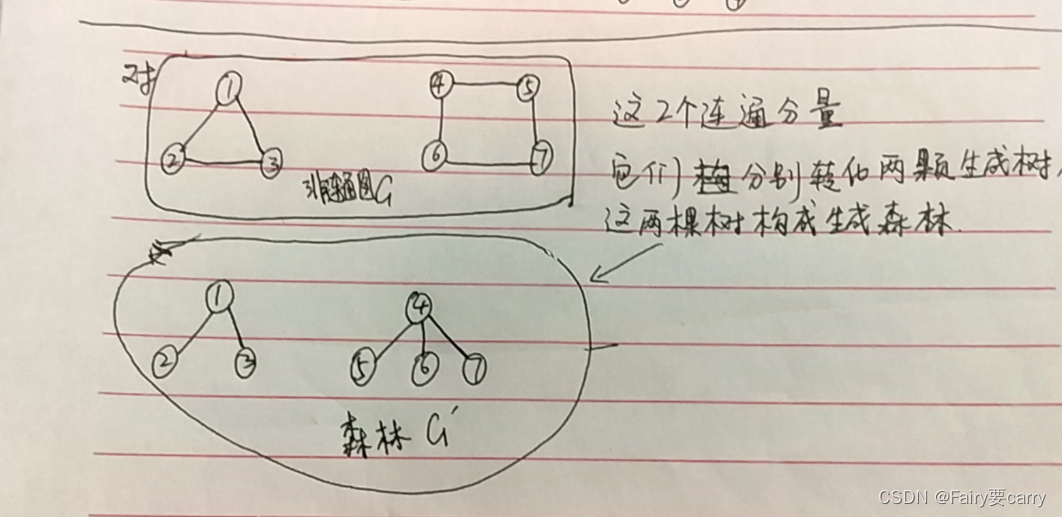
8.生成森林:
9.有向樹
一個頂點的入度為0,其余頂點入度為1的有向圖為有向樹
例題
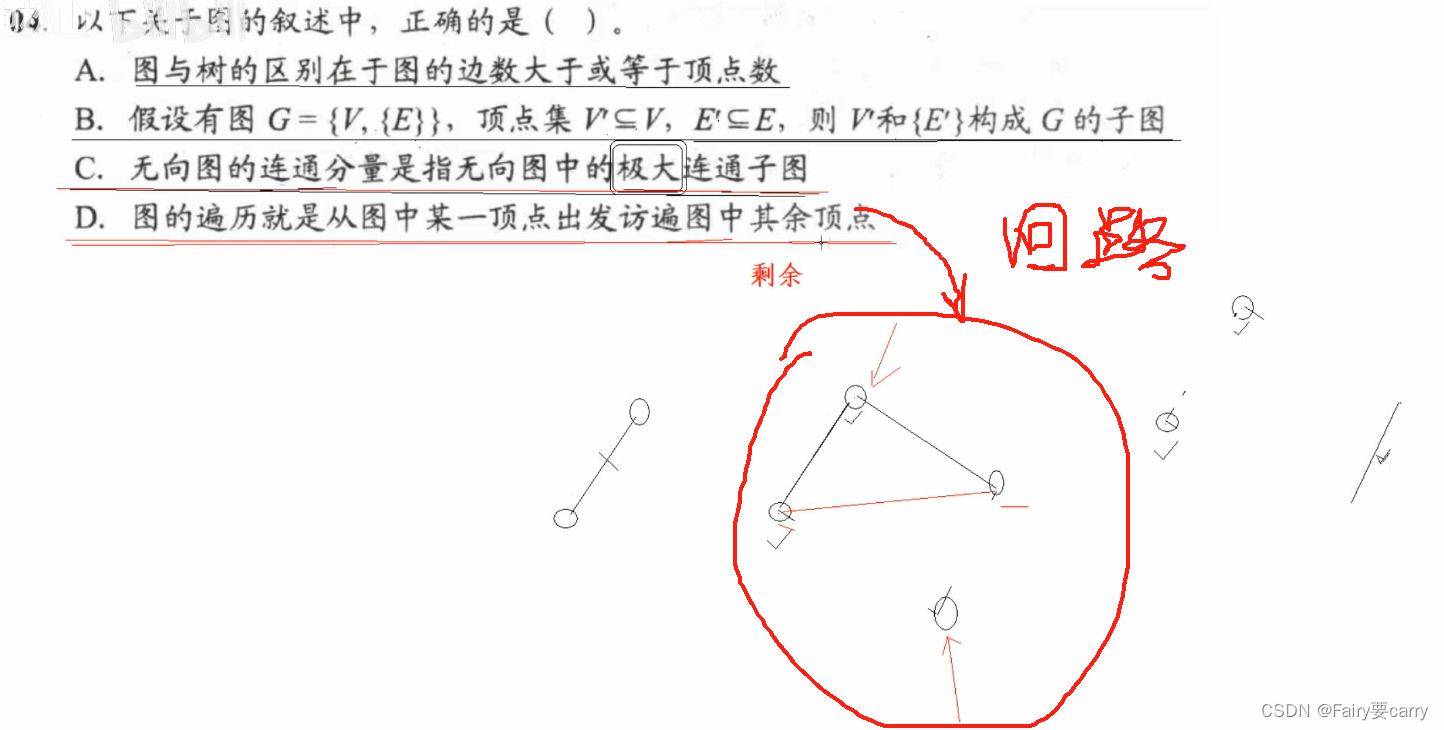
1.

2.
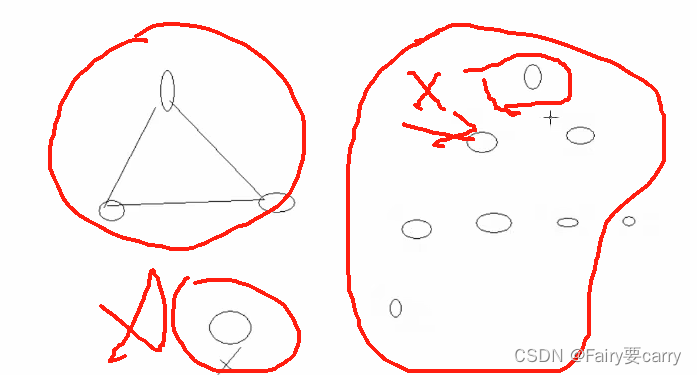
答案選B:
無向圖:是沒有方向的,而強連通圖 強調的是有方向的圖
而有回路,也不一定正確,可能會出現以下情況:訪問不到其余節點
而一棵樹,只有從根節點出發才能訪問所有節點

3.
1.子圖的概念:
**子圖:**假設有兩個圖G=(V,{E})和g=(v,{e}),如果v?V,e?E,則稱g為G的子圖;
例:假設有圖G=(V,{E}),頂點集A?V,B?E,則A和{B}構成G的子圖。答:錯誤,因為A和B未必能構成圖。定義中g是G的子圖,是因為給條件時已經明確g是圖
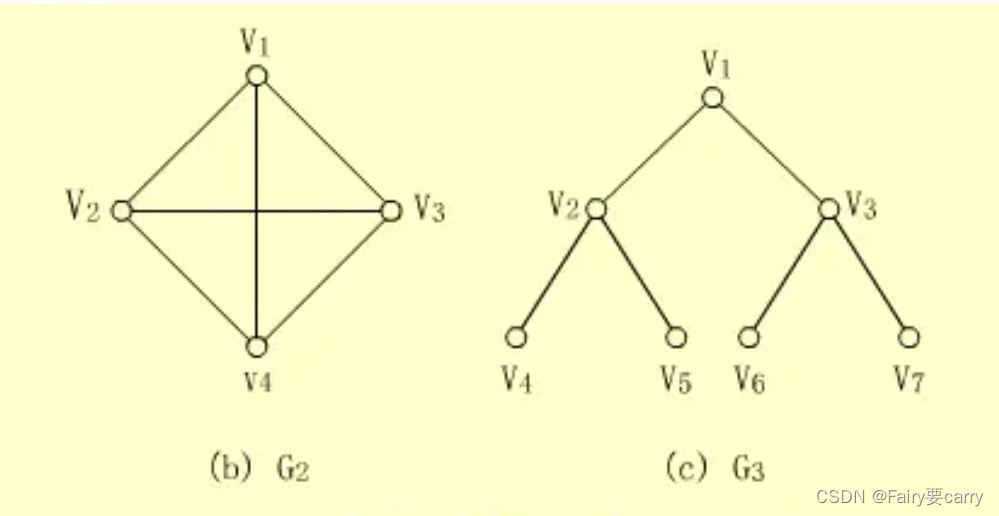
2.無向完全圖和有向完全圖的概念:
無向完全圖:每個節點之間都有邊,為1/2(n(n-1));
有向完全圖:任意兩個頂點之間都存在方向相反的兩條弧。n(n-1);
3.
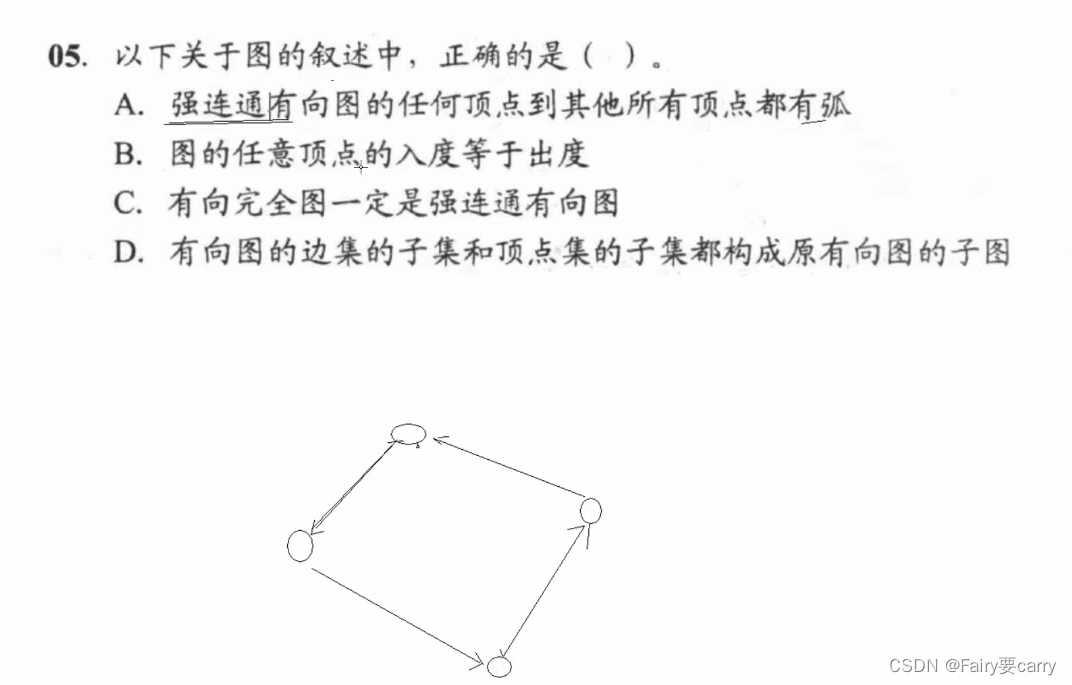
強連通圖的概念:
有方向,有邊,但是強連通圖不能保證任何頂點到其他所有頂點都有弧,可能只與其中之一之間有弧
圖的入度和出度:
圖的入度和出度不一定相等,入讀可能為0
有向完全圖:
有邊且方向為雙向,邊數為n(n-1),故有向完全圖一定為強連通圖 (有邊有方向)
有向圖邊集的子集和頂點的子集不一定能夠構成子圖:除非明確給出這個子集構成了個圖
5.
注意非連通的情況

6.
對于強連通有向圖,成一個環,三個節點三條邊
你到我有路徑,我到你有路徑——>最少邊數為n(環),至多邊數為n(n-1);

7.
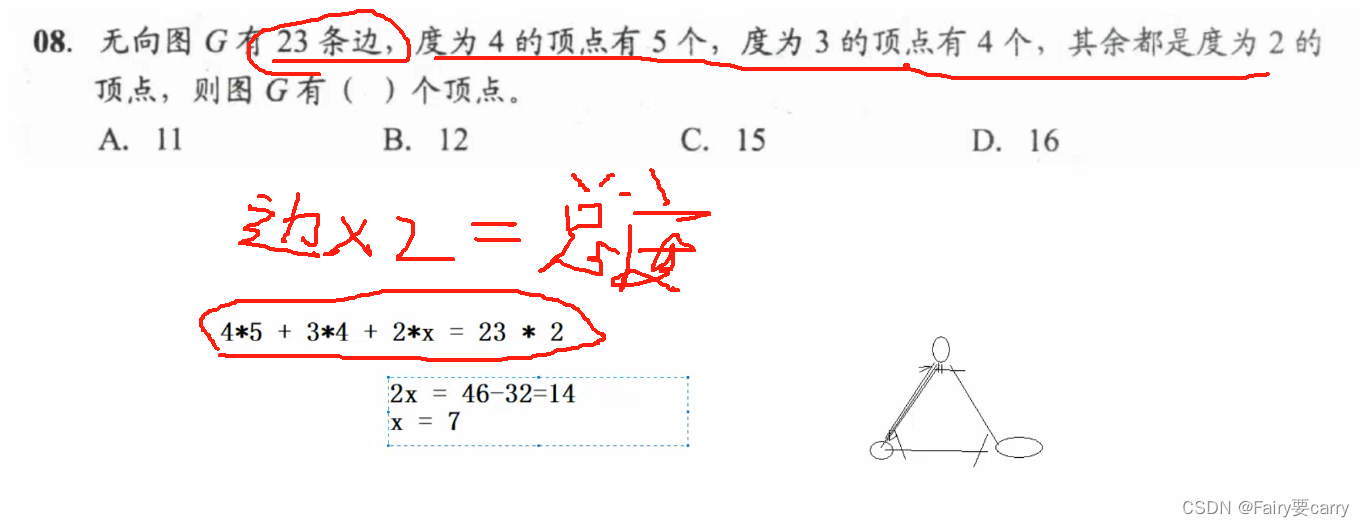
8.
n個頂點最多n-1條邊,算入度出度,2*(n-1)

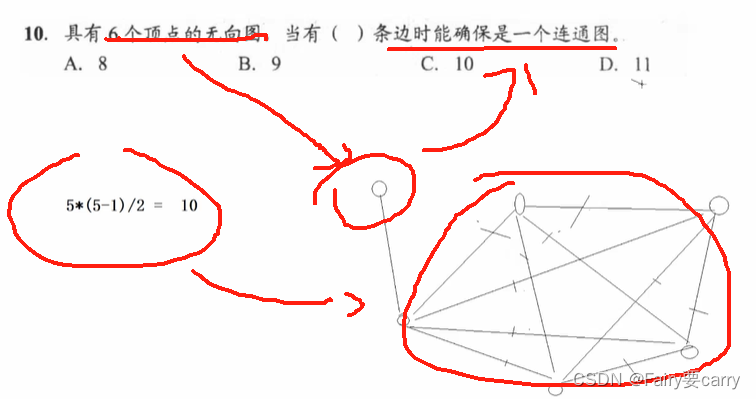
10.
在五個頂點的完全圖基礎之上再加一個頂點使其為連通圖
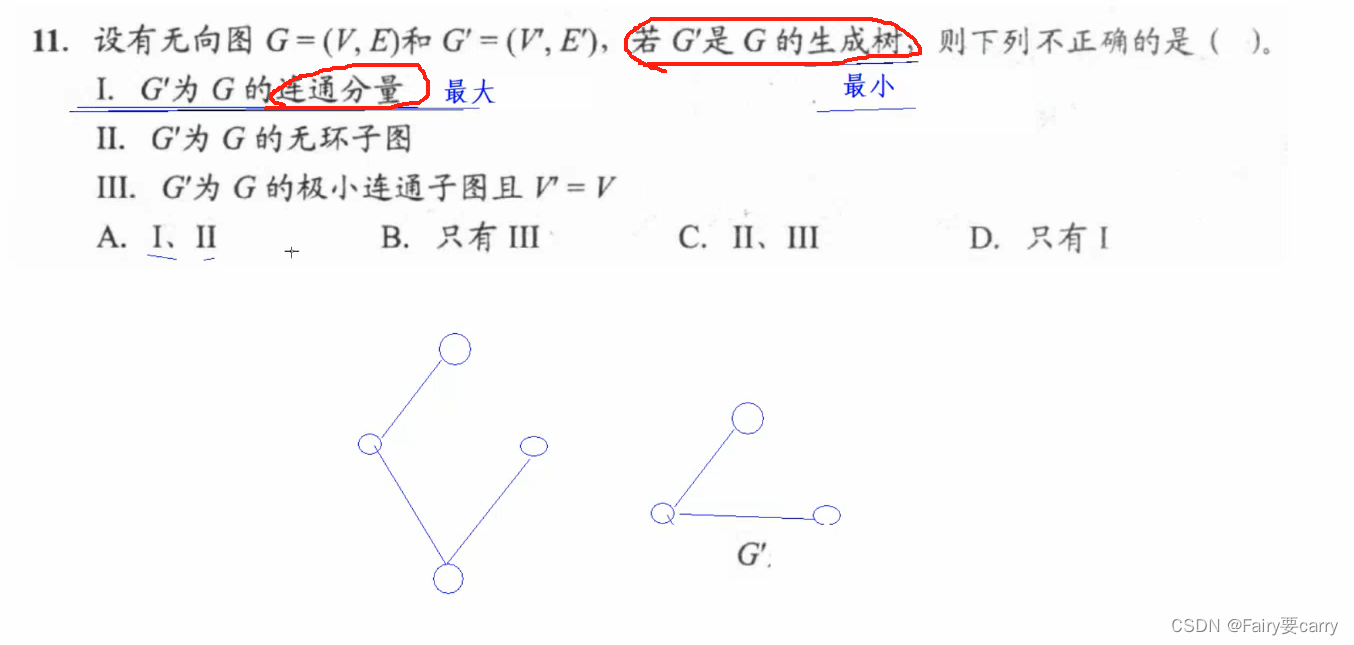
11.
可以知道的是樹一定是一個連通圖——>所以符合n個節點n-1條邊
- 生成樹指的是最小連通子樹,而連通分量指的是極大連通子樹
- 生成樹確實是無環的
- 生成樹與最下連通子樹相關
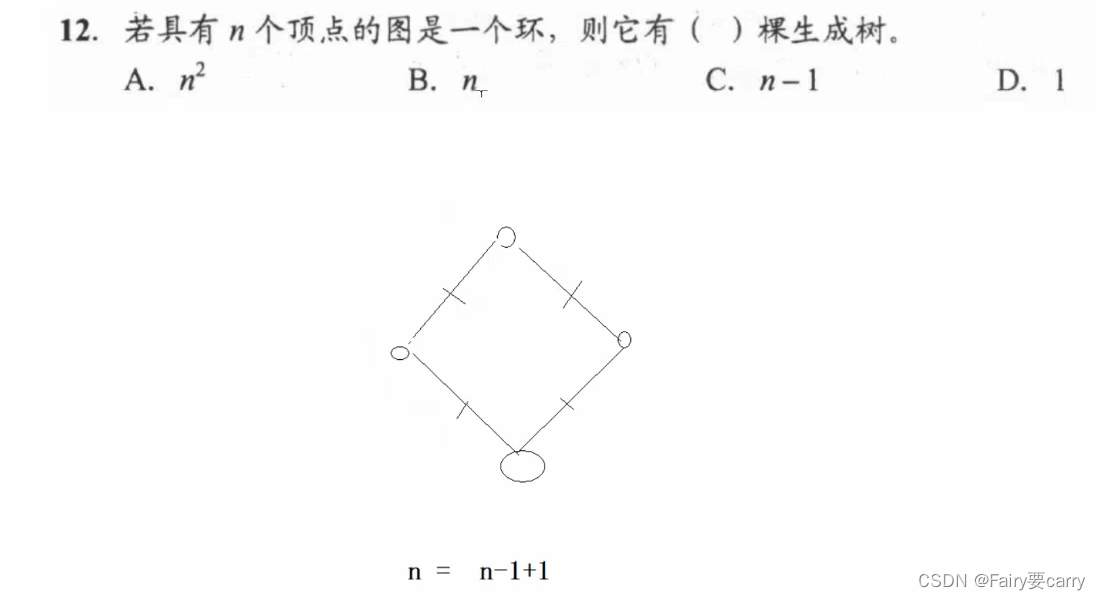
12.
n個頂點,成為一個環,有n個邊,n個邊有n顆生成樹(也可以從度方面思考)
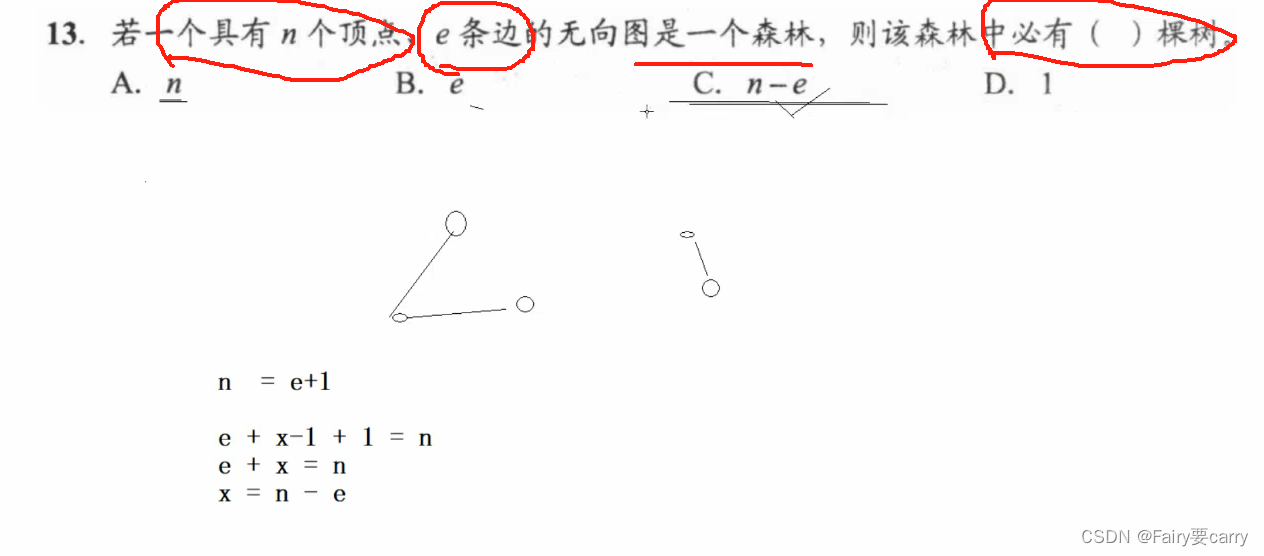
13.
設森林中有s棵樹,再用n-1條邊就能把所有的樹連接成一棵樹,此時,邊數+1=頂點數,即e+(x-1)+1=n => x=n-e
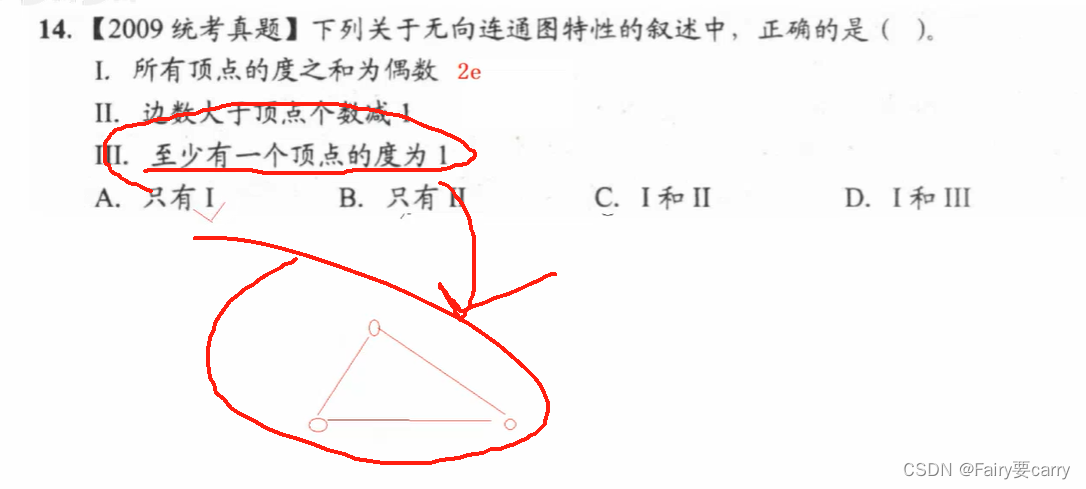
14.
在有向圖中,頂點的度為入度與出度之和。n個頂點的有向圖中,任一頂點最多還可以與其他n—1個頂點有一對邊相連。 2(n-1)*
15.
若圖為環,則度最少為2
16.
與上述類似,一個無向圖若要有七個節點,要保證它是連通的,說明六個節點的時候是完全圖,所以邊數為6*(5)/2,但因為要將其變為連通圖,所以需要+1條邊

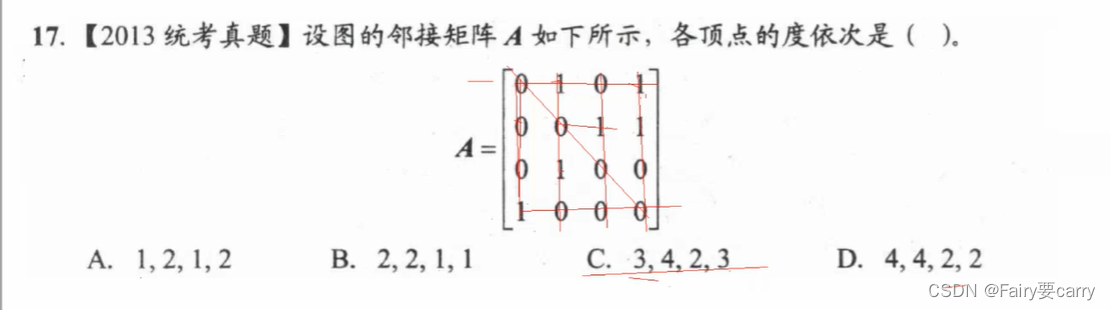
17.鄰接矩陣:
非對稱的鄰接矩陣,說明為有向圖,(因為無向圖一定是對稱的),各頂點的度依次是=入度+出度,為3423
如果是無向圖,就要/2;
2.圖的存儲
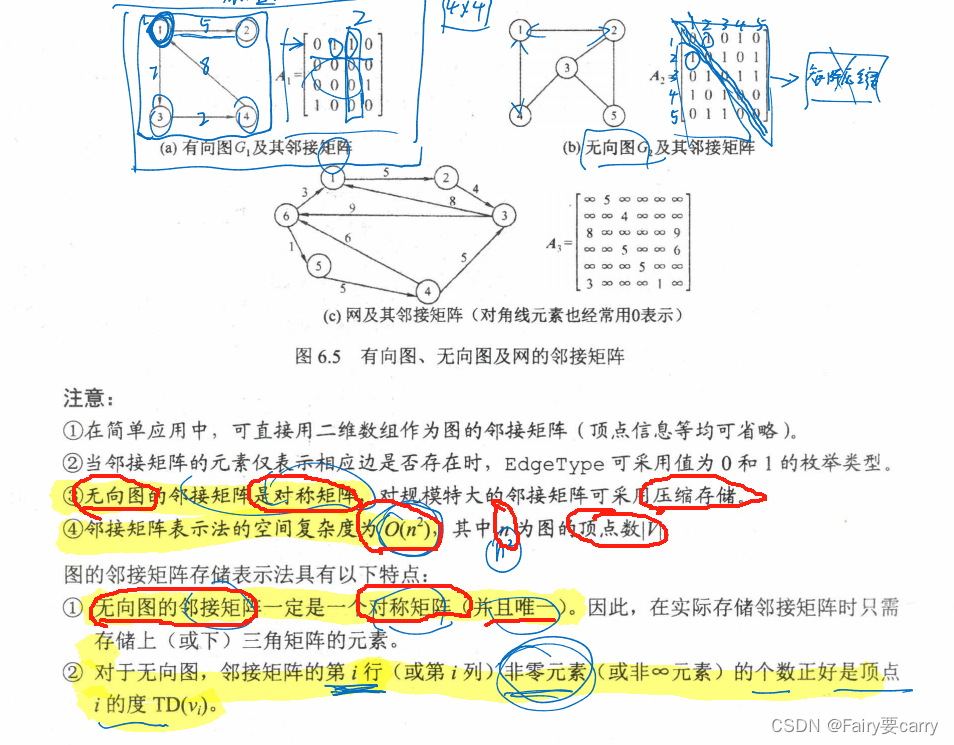
鄰接矩陣
無向圖的鄰接矩陣是唯一的;鄰接表是唯一的
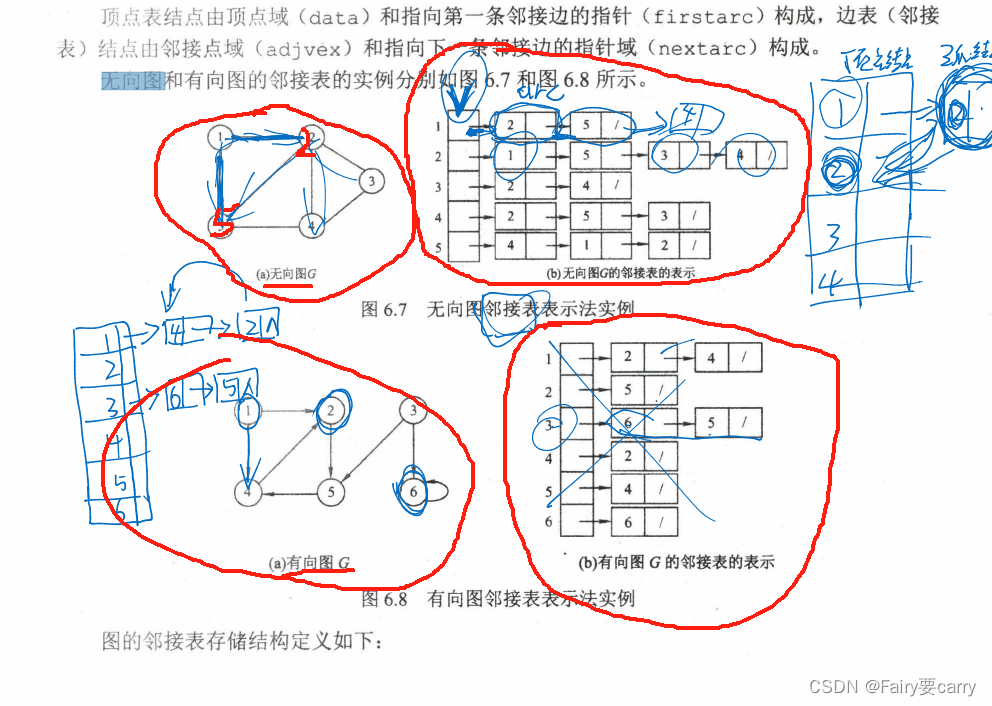
鄰接表
**前提:**因為鄰接矩陣較為稀疏,所以我們用鄰接表法減少空間的消耗
-
有向圖,無向圖都能夠存儲
-
鄰接表存儲有向圖時,頂點的出度個數為單鏈表中的節點個數
-
無向圖中,鄰接表不唯一,若無向圖中有n個頂點、e條邊,則其鄰接表需要n個頭結點和2e個表結點。適宜存儲稀疏圖。
-

-
無向圖和有向圖存儲空間的比較
**無向圖:**頂點數+2*邊數;**有向圖:**定點數+邊數

圖的遍歷
深度優先DFS:
從上至下遍歷,如果到頂了(已經走過的路就不走了),就返回上一步節點
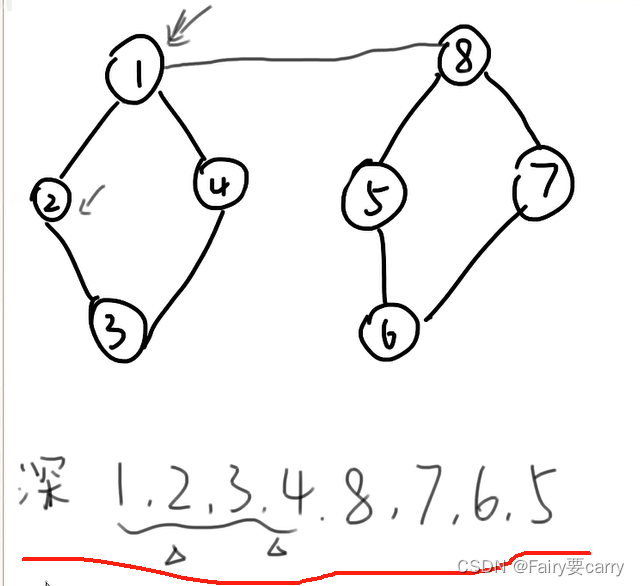
廣度優先BFS:
從左到右一層一層遍歷,放入(找當前節點距離為1的節點們,放入,然后繼續遍歷)
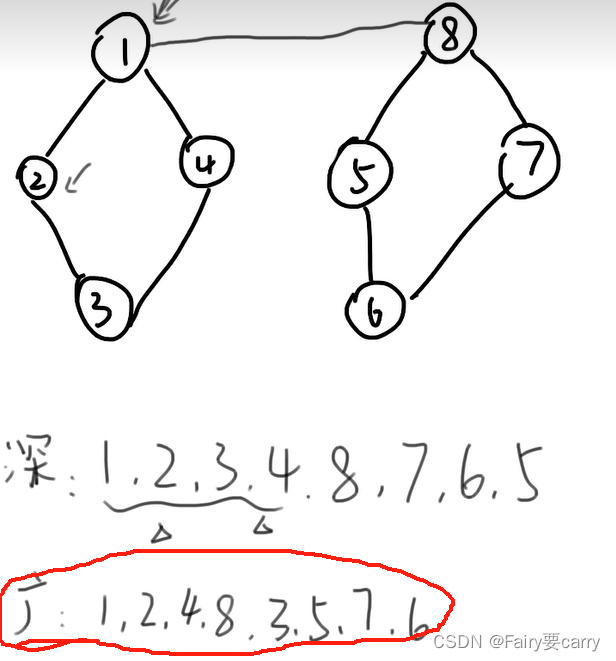
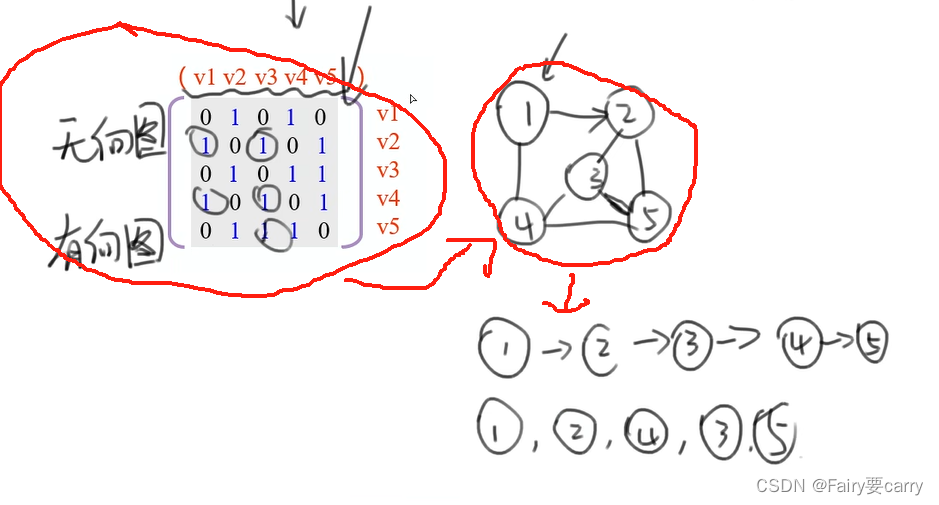
鄰接矩陣的遍歷:
注意遍歷的唯一性

 + Pycharm 錯誤(無法啟動)+ python 報錯)
)


 和 puts() 有兩個小區別))









—— 實用小函數總結)



