首先我們的目標是讓 s[i][j]表示為其左方和上方形成的矩陣所有元素的和

加上s[i-1][j]和s[i][j-1]后 s[i-1][j-1]部分重復了所以減去

最后加上a[i][j]即可完成目標?

s[i][j]=s[i-1][j]+s[i][j-1]-s[i-1][j-1]+a[i][j];

然后看題目要求

要求x1,y1,x2,y2圍成的小正方形內的元素和

我們利用剛剛處理好的s[i][j]來操作

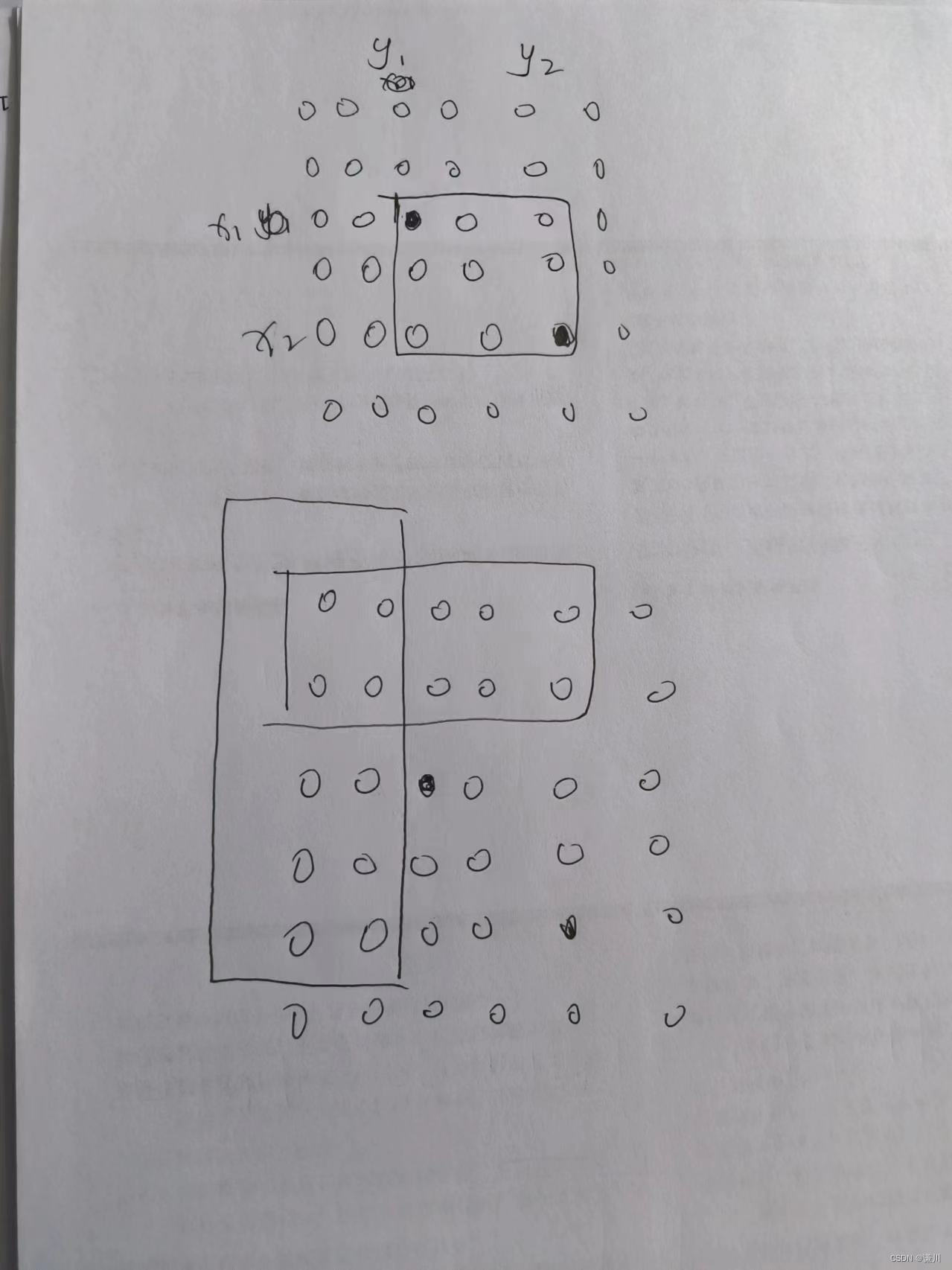
將是s[x2][y2]圈成的大正方形里面扣掉這兩塊

即s[x2][y1-1]和s[x1-1][y2]

最后加回去重復減去的s[x1-1][y1-1]即可?

所以式子為?s[x2][y2]-s[x2][y1-1]-s[x1-1][y2]+s[x1-1][y1-1]；

代碼

#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>
using namespace std;
const int N=1010;
int a[N][N],s[N][N];

int n,m,q;
int main(){
?? ?cin>>n>>m>>q;
?? ?for(int i=1;i<=n;i++)
?? ?{
?? ??? ?for(int j=1;j<=m;j++)
?? ??? ?{
?? ??? ??? ?cin>>a[i][j];
?? ??? ??? ?s[i][j]=s[i-1][j]+s[i][j-1]-s[i-1][j-1]+a[i][j];
?? ??? ?}
?? ?}
?? ?while(q--){
?? ??? ?int x1,y1,x2,y2;
?? ??? ?cin>>x1>>y1>>x2>>y2;
?? ??? ?cout<<s[x2][y2]-s[x2][y1-1]-s[x1-1][y2]+s[x1-1][y1-1];?
?? ?}
?? ?
?? ?return 0;
}