目錄
案例一——Hybrid A*(基于正向運動學)
1、基本思想
2、 實現流程
?3、啟發函數設計
4、分析擴張(Analytic Expansions)?
5、分級規劃(Hierarchical planning)
案例二——State Lattice Planning(基于逆向運動學)
1、基本思想
2、Conformal Lattice
3、目標狀態實例
4、生成路徑集合
5、代價值評估與路徑選擇
案例比較
案例一——Hybrid A*(基于正向運動學)
1、基本思想

? ? ? ? Hybrid A*是A*算法的一種擴展,本質也是一種圖搜索算法,Hybrid A*有以下特點:
- 通過在控制空間中實時構件狀態圖
????????整體思想是在控制空間中采樣利用前向積分的方式生成多條運動基元作為狀態圖的邊。以自行車模型為例,輸入量有兩個,分別是運動速度v和前輪轉角φ,為了簡化過程可以假設速度恒定,此時只需要考慮φ一個變量,可以假設φ∈[-umax, umax],對其做等距的離散采樣(上圖采樣了三份,實際應用當中會分成跟多份),取得的三個控制量分別為-umax,0和umax,然后對這三個控制量進行前向仿真/積分(給定初始狀態量,給定時間△t通過積分得到新的狀態);
- 在網格地圖中修剪一些節點,減少圖的大小(剪枝)
? ? ? ? 若在采樣時狀態空間取的足夠密(采樣等距距離足夠小),那么會導致圖中的節點和邊過多,極大地消耗計算資源,因此為了保證整體算法的實時性,Hybrid A*采用剪枝的操作,將狀態空間進行離散得到網格,若多個state落入同一個網格中,那么就選擇最優的一個state(cost最小)保留;
- 使用與A*算法相同的方法在狀態圖上搜索路徑
????????A*算法與Hybrid A*算法的比較:

- A*將代價值與網格中心聯系,并且只訪問與網格中心相對應的狀態;
- Hybrid A*為每一個網格賦予了連續的狀態(通過在模型的控制空間中采樣并積分得到),每一個網格對應的分數是其關聯的連續狀態下的代價值。
2、 實現流程
下面用偽代碼的方式對Hybrid A*算法的實現流程進行簡要描述:
Algorithm Astar(G, start):let open_list be priority queue;g[start] := 0;f[start] := g[start] + h[start];open_list.push(start,f[start]);while (open_list is not empty):current := open_list.pop();mark current as visitedif current is the goal:return current;// 通過從控制空間采樣和前向仿真來擴展鄰居節點for all unvisited neighbours next of current in Graph G:next_cost := g[current] + cost(current,next);if next is not in open_list:open_list.push(next,next_cost + h[next]) // 合并在離散空間中占用相同單元的連續坐標狀態else:if g[next] > next_cost:g[next] := next_cost;f[next] := next_cost + h[next];? ? ? ? 對于Hybrid A*算法,g(n)不單單表示路徑距離上的代價值,還包括一些其他方面的代價,比如方向改變(包括前后和左右)的懲罰項;
????????而對于啟發式函數h(n)的設置,可以用經典的歐幾里得距離或和曼哈頓距離,也可以用一些其它的方式使整體的搜索效率更高,這方面會在下面講解;
?3、啟發函數設計
? ? ? ? 在Practical search techniques in path planning for autonomous driving.?論文中作者給出了兩種啟發函數的設計,分別是:
- Non-holonomic-without-obstacles
? ? ? ? 這種啟發式函數的估計是基于Reeds Sheep Path的方法,此方法考慮了車輛本身的特性,卻忽略了環境;
- Holonomic-with-obstacles
? ? ? ? 這種啟發式函數的估計是基于目標節點和當前正在擴展的頂點之間的最短距離,此方法忽略了車輛本身的特性,只考慮了障礙物。
? ? ? ? 原論文中給出了兩個特定場景下使用不同的啟發式函數取得的效果,如下圖所示:

? ? ? ? (a)使用最簡單的歐幾里得距離作為啟發式函數
? ? ? ? (b)使用non-holonomic-without-obstacles作為啟發式函數
? ? ? ? (c)使用non-holonomic-without-obstacles作為啟發式函數
? ? ? ? (d)non-holonomic-without-obstacles和Holonomic-with-obstacles組合使用
? ? ? ? 通過(a)圖和(b)圖的比較,可以得到相比與簡單使用歐幾里得距離,使用non-holonomic-without-obstacles作為啟發式函數使樹節點縮小了接近十倍,效率有顯著的提升;
? ? ? ? (c)(d)圖中是一個更為復雜的場景,(c)圖表示在復雜場景下單純使用non-holonomic-without-obstacles作為啟發式函數會導致樹的規模很大,因為沒有考慮環境障礙物的因素,需要把環境探索完全才能得到可行的路徑;
????????而將non-holonomic-without-obstacles和Holonomic-with-obstacles組合進行使用就能得到(d)圖所示的路徑,有前面的學習可知通過一次完整的迪杰斯特拉算法可以實現圖中某個節點到其他所有節點啊之間的距離,利用這個性質,在做Hybrid A*算法前,先從終點反向的進行一次迪杰斯特拉算法對整個圖進行遍歷我們可以得到圖中任意節點到終點的最短路勁(考慮障礙物),將節點距離記錄在表格中(前期的離線收集過程)。然后在Hybrid A*算法實時的搜索時直接根據當前位置從表格中獲取對應的離終點考慮障礙物的最短路徑。
4、分析擴張(Analytic Expansions)?
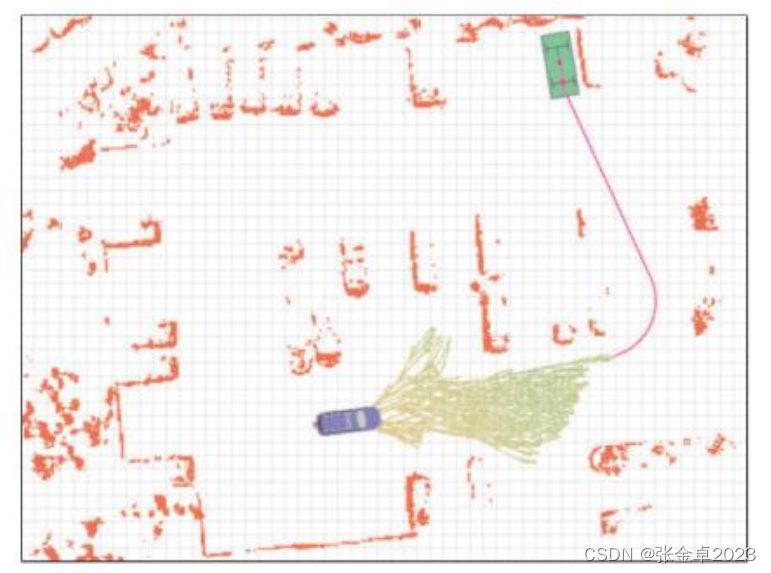
? ? ? ? ?論文指出離散搜索(前向積分)永遠無法達到精確的連續目標狀態(整體的精度還取決于A*網格的分辨率),因此文章中使用Reeds Shepp Path解析地連接當前節點和目標節點,利用這種方法可以大大提高障礙物在稀疏環境下的搜索速度。
5、分級規劃(Hierarchical planning)

? ? ? ? ?在一個復雜的狀態空間下想要一次性找到兩點之間的最優軌跡是比較困難的,分級規劃的思想就是利用分布的思路,先利用某種方式(上圖是利用Hybrid A*)獲得一條初解(全局最優解),再基于初解做局部的平滑得到局部最優解。
? ? ? ? 由Hybrid A*得到的路徑通常是次優的,主要有兩個原因:一是在剪枝的過程中,每一個柵格內都只保留一個state,這種操作會導致在某種層面上不是最優的;二是在控制空間采樣時,不管是對前輪轉角(方向盤轉角)或者是轉角變化率進行采樣,都無法實現嚴格意義上的連續,最終的結果可能并不是很平滑。因此需要進一步改善。
? ? ? ? 論文中通過采用共軛梯度下降法對Hybrid A*路徑進行光滑處理。
案例二——State Lattice Planning(基于逆向運動學)
1、基本思想

? ? ? ? 在狀態空間中采用獲得終點狀態(一系列離散的點)?,可以在Frenet坐標系下采樣,也可以在Cartesian坐標系下采樣,再通過求解邊界值(BVP)問題來獲得運動基元,通過計算每條路徑的成本選擇最佳路徑。
2、Conformal Lattice
? ? ? ? conformal lattice指的是在結構化道路上定義的一種采樣規則,大致是在在橫向上獲取目標狀態沿道路目標點橫向偏移采樣,在縱向上沿著車道中心線行駛,能夠在避開障礙的同時加快規劃過程。
3、目標狀態實例
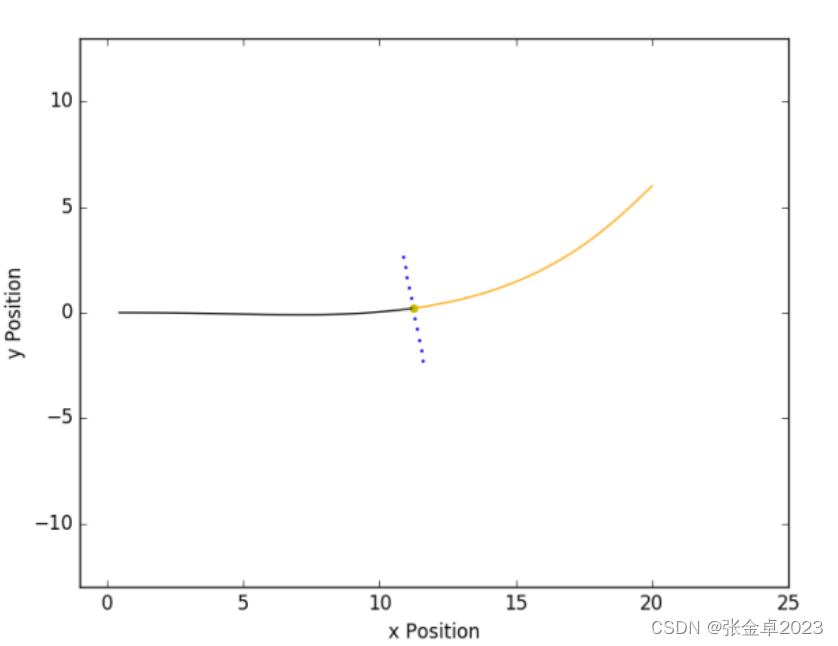
? ? ? ? 目標狀態從目標點沿道路橫向偏移采樣,具體的采樣規則需要根據當前速度和其他因素進行調整。比如在縱向上生成的路徑的長度(弧長)往往需要和車速關聯,在低速時往往希望弧長短一些,因為在低速時弧長過長會使車輛運動對應位置時失去時效性;而在高速時往往希望弧長長一些,弧長過短不利于下一時間對環境事物的判斷。
? ? ? ? 另一方面,在側向方向上的采樣也有特定的策略,比如在擁堵場景下,采樣距離過大可能會導致無解。
4、生成路徑集合
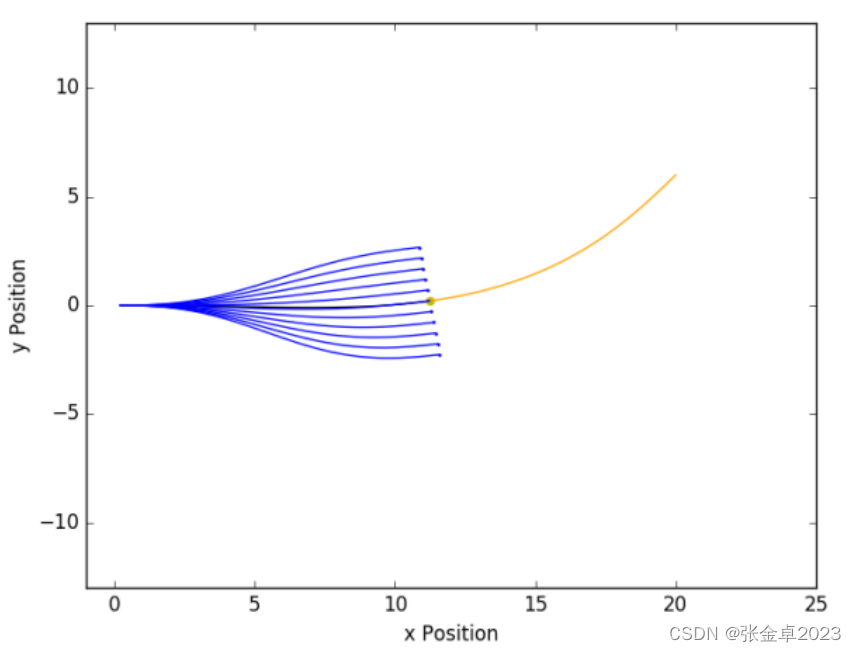
?????????在采樣結束后,要進行邊界值問題(BVP)處理,在Frenet坐標系中可以用五次多項式進行處理,在Cartesian坐標系中可以用三次螺旋線進行處理。
5、代價值評估與路徑選擇
? ? ? ? 代價函數的設計往往要考慮多個方面,為了簡化問題可以簡單考慮安全性、平滑性和對中心線的貼合度三個方面的代價函數考慮:
- 安全性:
- 平滑性:
- 中心線貼合度:
?
? ? ? ? 將這三個因素進行不同的權重進行組合,計算總的代價函數:
? ? ? ? ?得到了代價函數后就可以評估生成的各曲線的代價值進而獲得最優路徑。
案例比較
? ? ? ? 案例一是基于正向運動學的方法,案例二則是基于逆向運動學的方法,下面介紹這兩種運動學方法以及它們的對比。
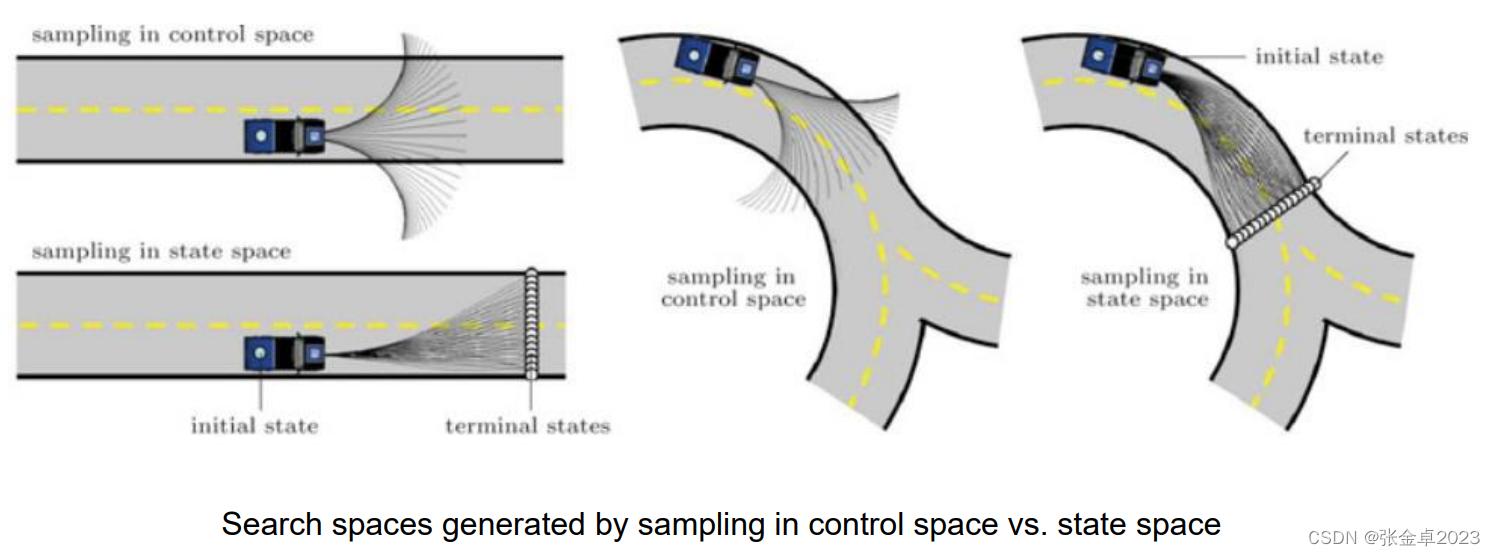
? ? ? ? 正向運動學方法對應上圖中的在控制空間采樣,在知道控制量v、u以及給定時間t通過前向積分的方式得到一系列的軌跡;而逆向運動學對應上圖中在狀態空間中采樣,此時的輸入量是起始和終點的狀態量,通過起點和終點的狀態量反推中間的狀態量和輸入量。
- 正向運動學(控制空間采樣)
????????優點:只要給定初始狀態和控制變量,通過運動學/動力學模型進行前向積分的方式即可得到? ? ? ? ? ? ? ? ? ? ?整個狀態軌跡;
????????缺點:缺少對目標點的引導,單純依靠啟發式函數來引導搜索過程。
- 逆向運動學(狀態空間采樣)
? ? ? ? 優點:具有較強的任務引導性,直接生成朝著目標的采樣狀態;
? ? ? ? 缺點:BVP問題較難處理?,并且采樣的規則需要精心計算。

)
)
)
)
的演進)






![[技巧]Arcgis之圖斑四至點批量計算](http://pic.xiahunao.cn/[技巧]Arcgis之圖斑四至點批量計算)




策略模式)

之數據校驗)