前言

有人說設計出AVL樹的的人是個大牛，那寫紅黑樹（RBTree）的人就是天才！
上一篇文章，我們已經學習了AVL樹，牛牛個人認為AVL樹已經夠優秀了，那讓我們一起探究一下，為什么紅黑樹比AVL樹的結構還要優秀吧！

一、紅黑樹的介紹

紅黑樹，是一種二叉搜索樹，但在每個結點上增加一個存儲位表示結點的顏色，可以是Red或Black。 通過對任何一條從根到葉子的路徑上各個結點著色方式的限制，紅黑樹確保沒有一條路徑會比其他路徑長出倆倍，因而是接近平衡的。

紅黑樹，是一種自平衡的二叉查找樹，它的性質比較復雜，但卻非常重要，常用于C++中的STL庫中的set、map等容器。紅黑樹的節點有兩種顏色：紅色（red）和黑色（black）。它具有如下五個性質：

1. 每個節點是紅色或者黑色的。
2. 根節點是黑色的。
3. 每個葉子節點（這里特指最下面的空節點）是黑色的。
4. 如果一個節點是紅色的，則它的子節點必須是黑色的。（即：每條路徑上不能出現連續的紅結點）
5. 從任一節點到其每個葉子節點的所有路徑都包含相同數目的黑色節點。

由于紅色結點的父親必須是黑色結點，并且每條路徑上的黑色結點的個數也必須相同，所以得到了紅黑樹最長路徑中節點個數不會超過最短路徑節點個數的兩倍

這也就決定了，紅黑樹的高度是log（n）級別的。
例如，下面這個就是紅黑樹

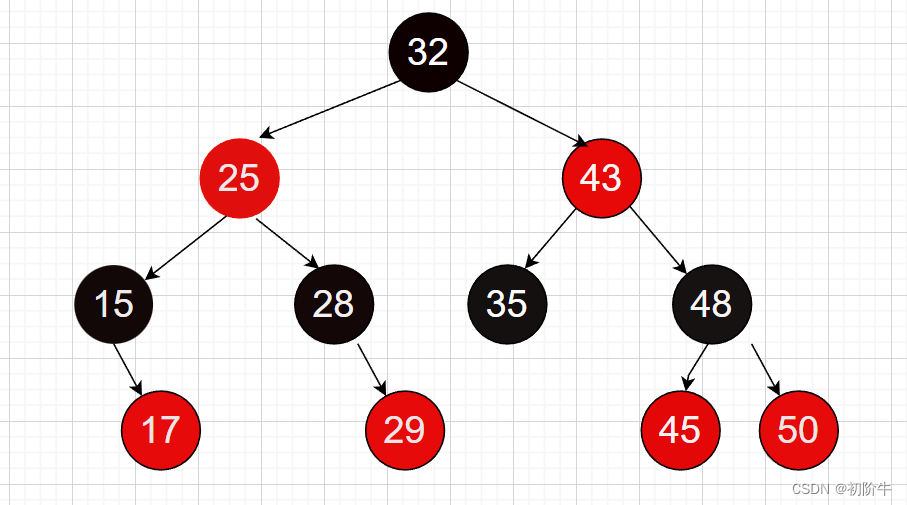
二、手撕紅黑樹

2.1 框架結構分析

2.11 結點顏色

紅黑樹較于AVL樹，不在使用平衡因子，而是增設了顏色變量，這里我們可以枚舉出這兩種顏色，方便使用。

	enum Colour	//枚舉出顏色{RED,		//紅色BLACK		//黑色};

2.12 結點類

同AVL樹一樣，紅黑樹也是三叉鏈

	//結點類template<class K, class V>struct RBTreeNode{//指針域RBTreeNode<K, V>* _left;RBTreeNode<K, V>* _right;RBTreeNode<K, V>* _parent;pair<K, V> _kv;	//數據域Colour _Col;RBTreeNode(const pair<K, V>& kv)//構造函數:_left(nullptr), _right(nullptr), _parent(nullptr), _kv(kv), _Col(RED)				//注意這里，默認新構造的結點是紅色的{}};

2.13 紅黑樹結構

	//紅黑樹的結構template<class K, class V>class RBTree{typedef RBTreeNode<K, V> Node;public:// 在紅黑樹中插入值為data的節點，插入成功返回true，否則返回false//此版本紅黑樹對于重復元素，插入失敗bool Insert(const pair<K, V>& kv);// 搜索紅黑樹中是否存在值為data的節點。//存在返回該節點的地址，不存在則返回nullptrNode* Find(const pair<K, V>& data);// 獲取紅黑樹最左側節點Node* LeftMost();// 獲取紅黑樹最右側節點Node* RightMost();//（這里的玩法大家應該不陌生了）	int Height();//計算紅黑樹的高度bool IsValidRBTRee();// 檢測紅黑樹是否為有效的紅黑樹private:bool _IsValidRBTRee(Node* pRoot, size_t blackCount, size_t pathBlack);int Height(Node* root);// 左單旋void RotateL(Node* pParent);// 右單旋void RotateR(Node* pParent);// 為了操作樹簡單起見：獲取根節點Node*& GetRoot();private:Node* _root = nullptr;};

2.2 接口實現

2.21 插入接口（重點）

本篇主要講解的部分就是紅黑樹的插入操作。

函數名 ：	insert
返回值	插入成功，返回true；插入失敗，返回false
形參	鍵值對

//插入函數
template<class K, class V>
bool RBTree<K, V>::Insert(const pair<K, V>& kv) {
}

（1）.如果是第一次插入，則插入的是根節點，則需要特殊處理，因為要給根節點root賦值。

在結點類中我們提到，在創建的新節點我們給與了默認顏色為RED（紅色），而紅黑樹的根節點必須是BLACK（黑色）的，這里一定要記得修改一下顏色。

//第一次插入if (_root == nullptr) {_root = new Node(kv);_root->_Col = BLACK;		//注意根節點一定是黑色的，默認構造的新節點是紅色的，所以這里要改一下。return true;}

(2) 尋找插入位置
紅黑樹也是二叉搜索樹，學到這里，相信友友們在AVL樹和二叉搜索樹學習階段，已經知道如何尋找插入位置。

	//尋找插入位置while (cur) {parent = cur;if (_root->_kv.first > kv.first) {cur = cur->_left;		//插入的值當前結點的值小，往左走}else if (_root->_kv.first < kv.first) {cur = cur->_right;		//插入的值當前結點的值大，往右走}else {return false;	//本篇實現的紅黑樹，對于重復值，插入失敗}}//判斷插入在左邊還是右邊cur = new Node(kv);if (kv.first < parent->_kv.first) {				//插入在左邊parent->_left = cur;}else {									//插入在右邊parent->_right = cur;}cur->_parent = parent;					//保證三叉鏈的關系

3.看uncle（叔叔）

叔叔（uncle）？這里我將當前結點的父親（parent）的兄弟稱為叔叔結點。

示例：

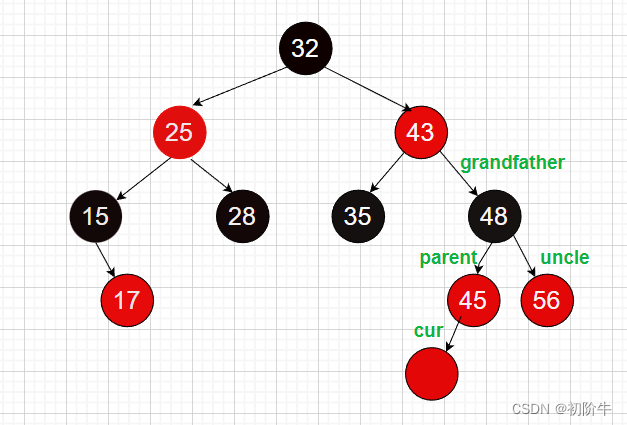
當我們新增一個結點時，默認新節點的顏色為RED，如果它的父親結點是黑色的，則不需要做任何調整，直接插入成功！

當父親結點是紅色的時候，則與新增結點一起，會構成連續的紅色結點，此時需要調整。

調整規則主要看uncle叔叔結點。

情況1： 父親是爺爺的左，cur結點是父親的左。 （左左）

👻情況：叔叔存在且為紅
🔑調整方案： 變色+向上更新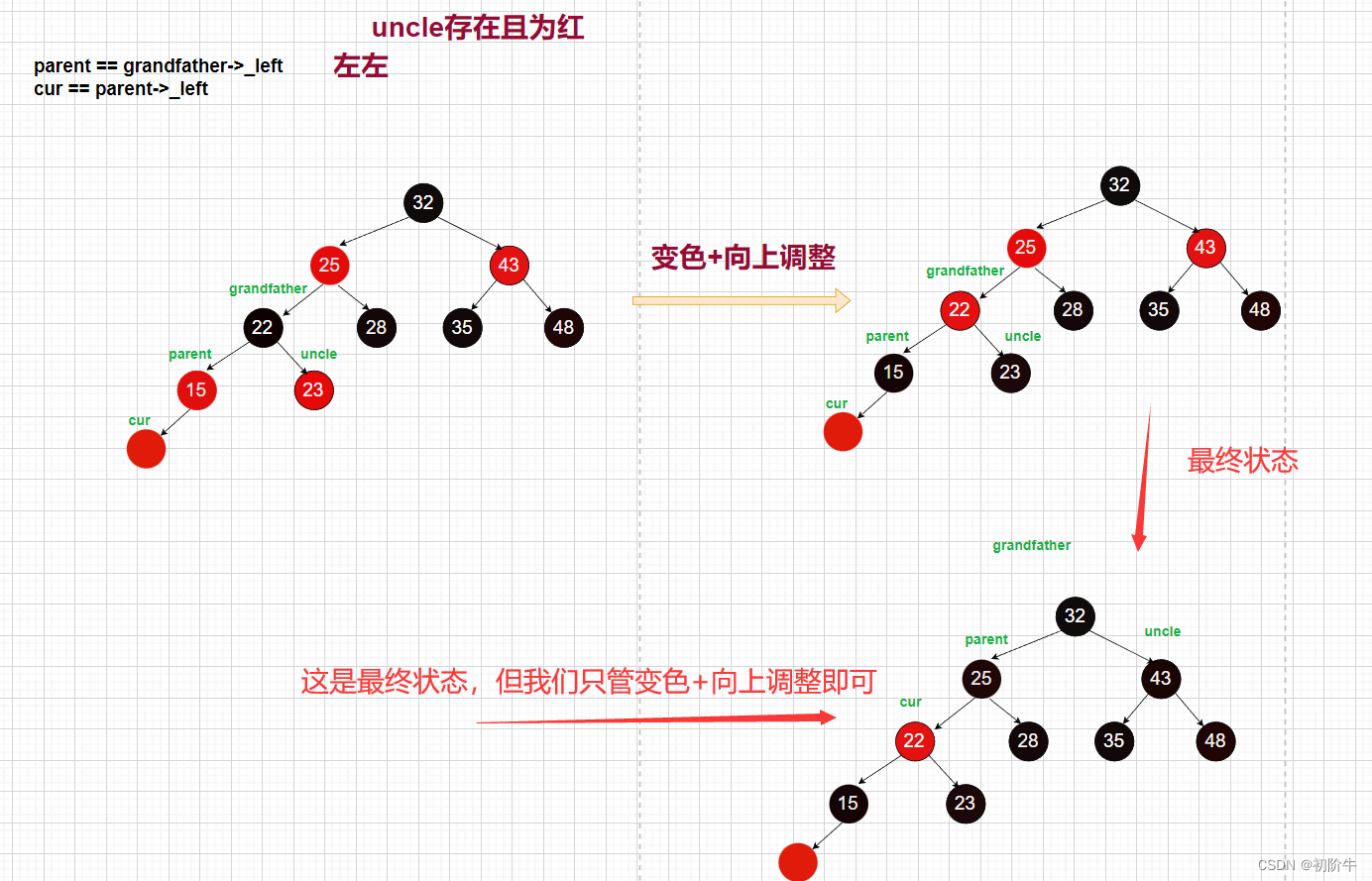（圖片為博主原創，請勿隨意轉發使用）

👻情況：叔叔不存在，或者存在且為黑
🔑調整方案： 右旋+變色

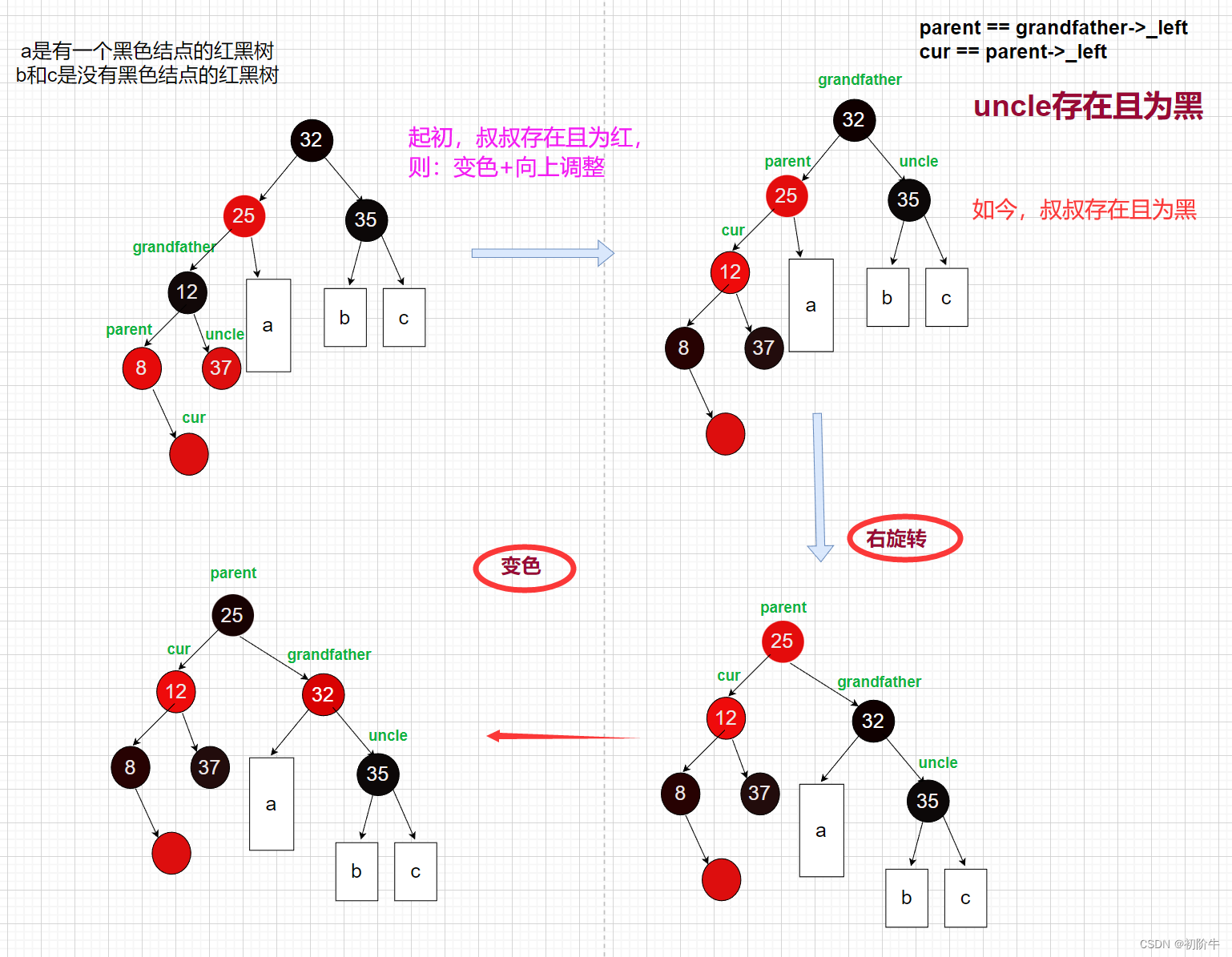（圖片為博主原創，請勿隨意轉發使用）

情況2： 父親是爺爺的左，cur結點是父親的右。 （左右）

👻情況：叔叔存在且為紅
🔑調整方案： 變色+向上更新
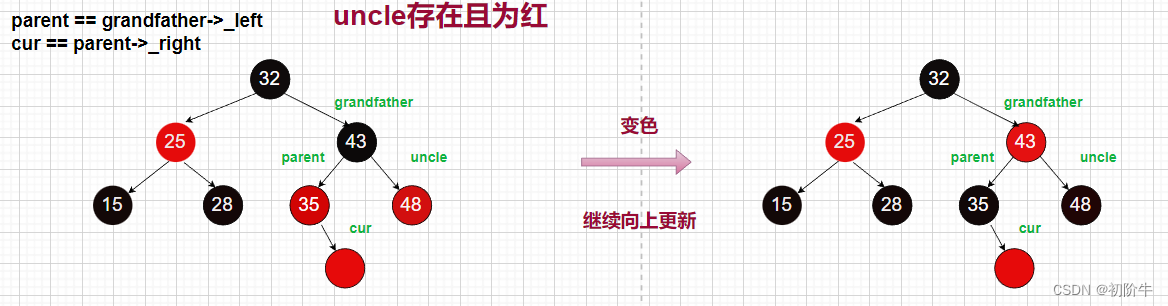（圖片為博主原創，請勿隨意轉發使用）

👻情況：叔叔不存在，或者存在且為黑
🔑調整方案： 左右雙旋+變色

示例圖：

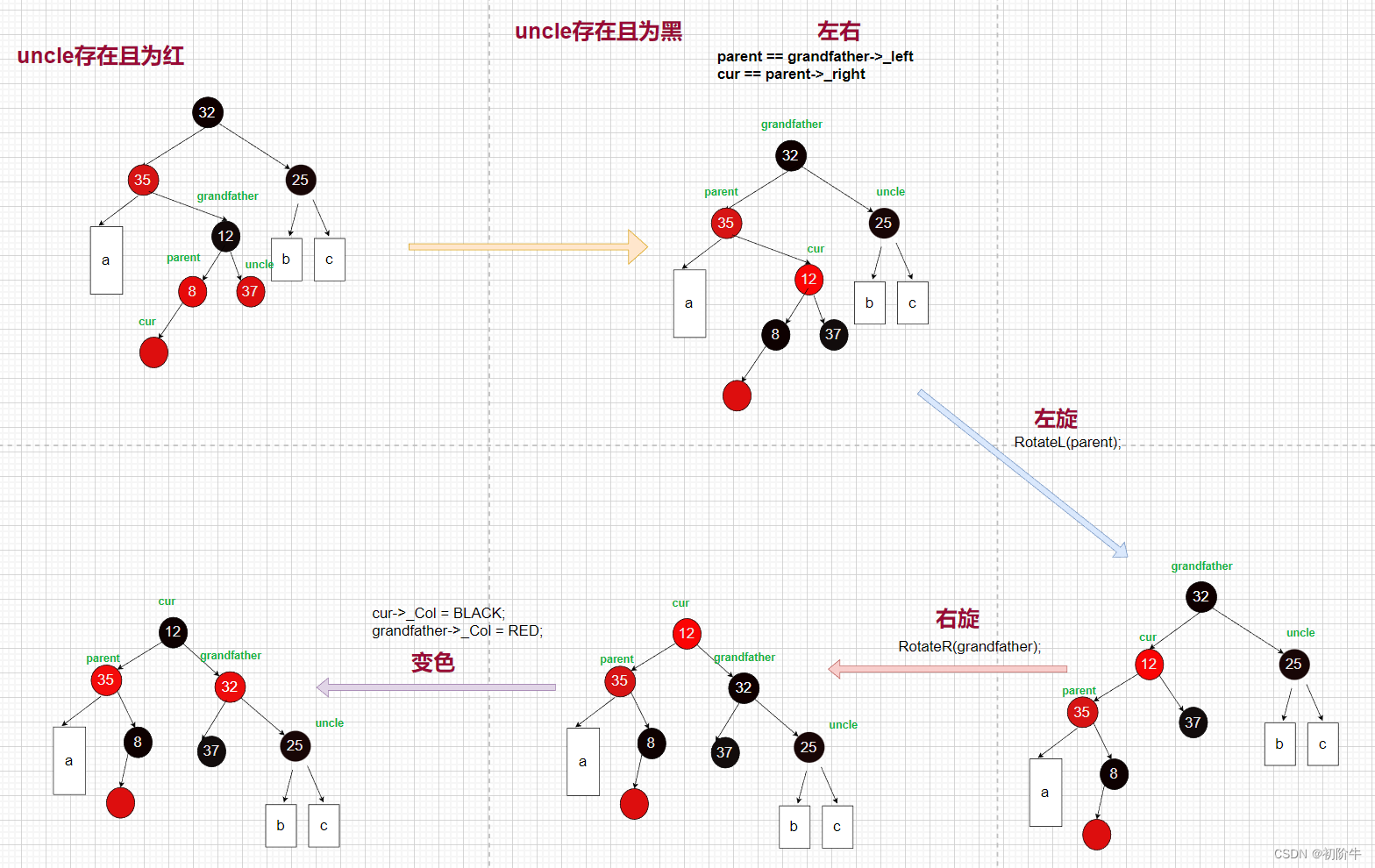（圖片為博主原創，請勿隨意轉發使用）

情況3： 父親是爺爺的右，cur結點是父親的左。 （右左）

👻情況：叔叔存在且為紅
🔑調整方案： 變色+向上更新
這里不畫圖了，牛牛畫累了。

👻情況：叔叔不存在，或者存在且為黑
🔑調整方案： 右左雙旋+變色

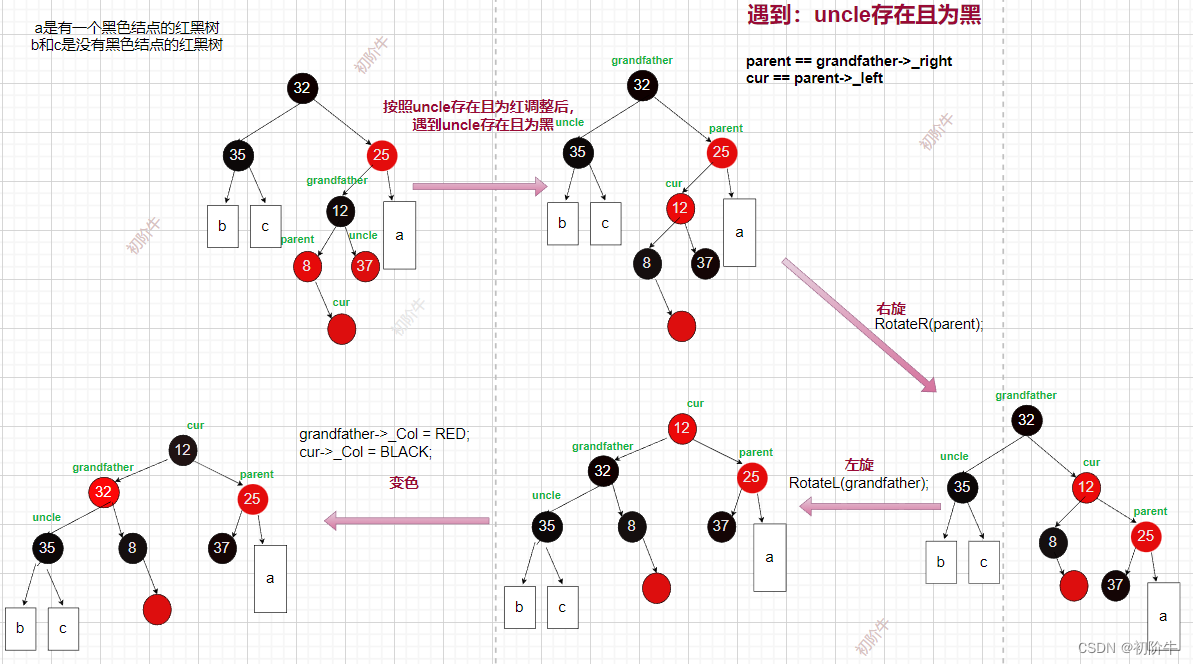（圖片為博主原創，請勿隨意轉發使用）

情況4： 父親是爺爺的右，cur結點是父親的左。 （右右）

👻情況：叔叔存在且為紅
🔑調整方案： 變色+向上更新
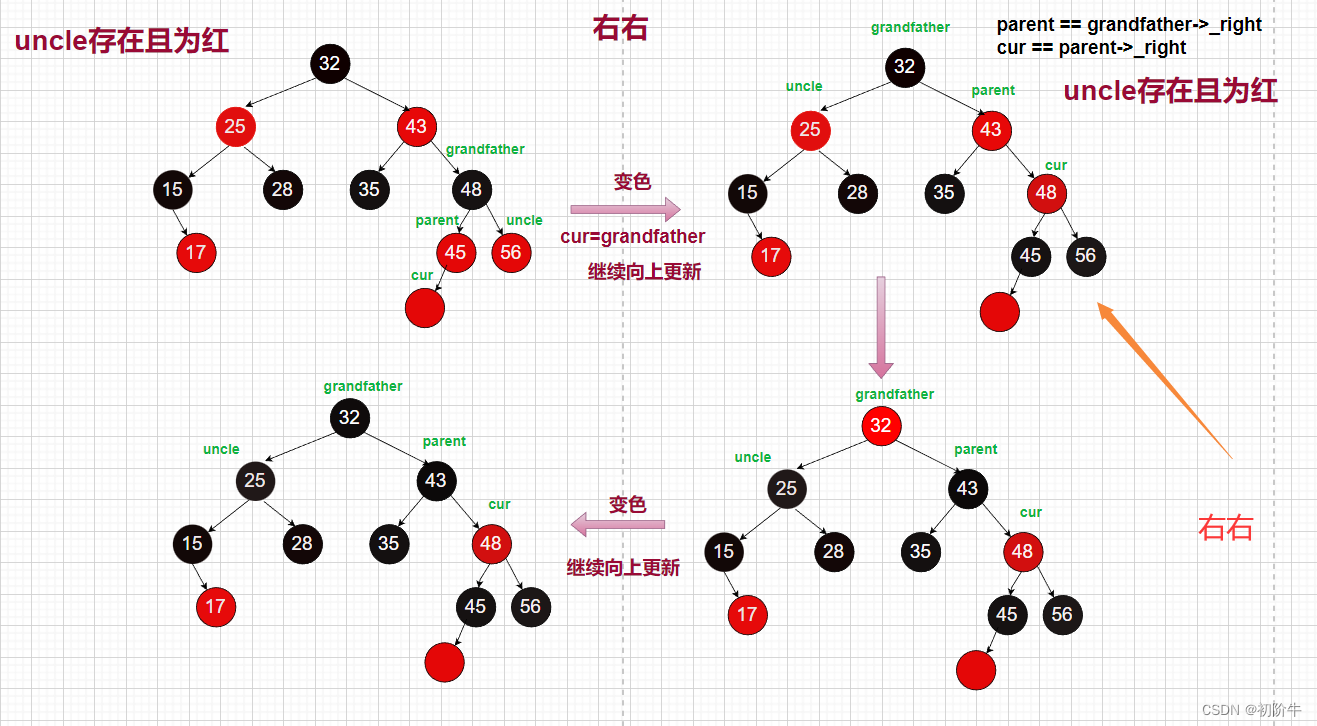（圖片為博主原創，請勿隨意轉發使用）

👻情況：叔叔不存在，或者存在且為黑
🔑調整方案： 左旋+變色
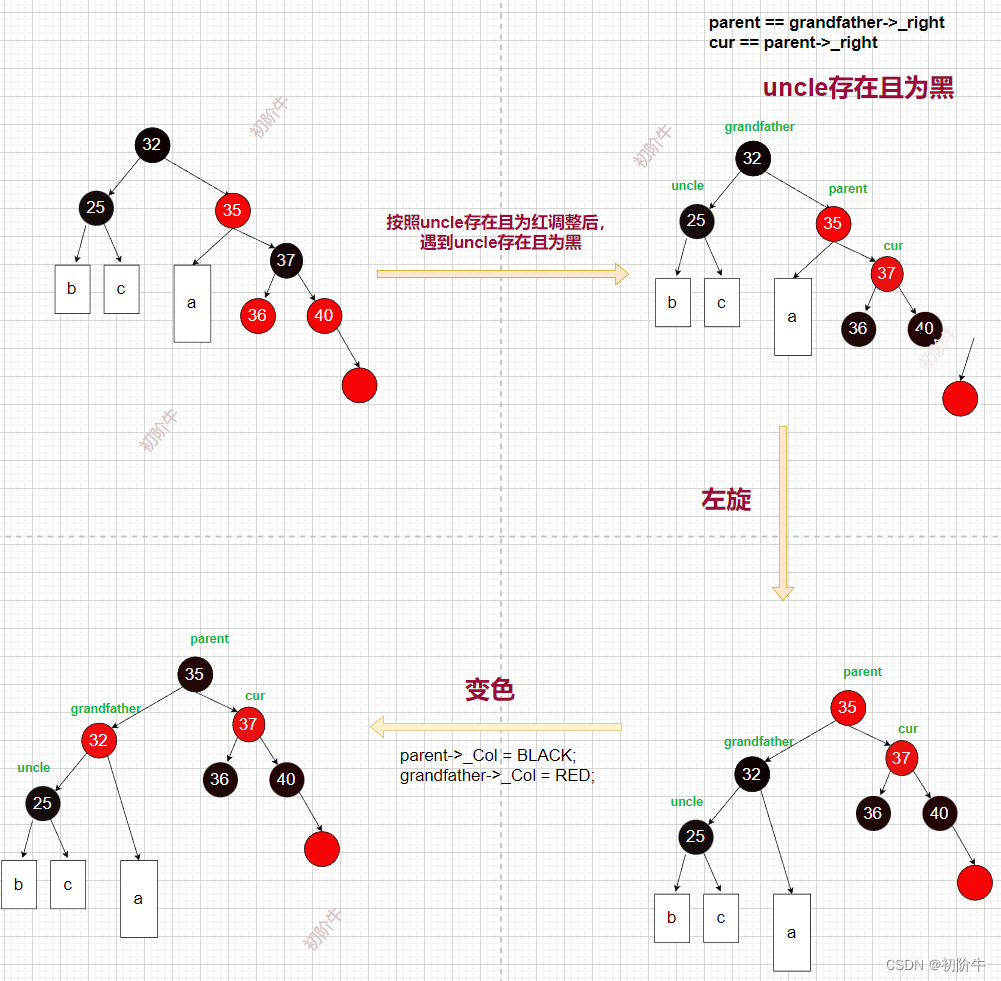（圖片為博主原創，請勿隨意轉發使用）

總結：
紅黑樹的插入主要看uncle
分為兩種情況：
（1）uncle存在且為紅
調整方案： 變色+繼續向上調整
（2）uncle不存在或者uncle存在且為黑
調整方案： 旋轉+變色

至于如何旋轉，因為紅黑樹沒有采用平衡因子的方式，所以我們采用判斷grandfather與parent 和 parent與cur的關系結構來決定。
下圖是具體調整總結：

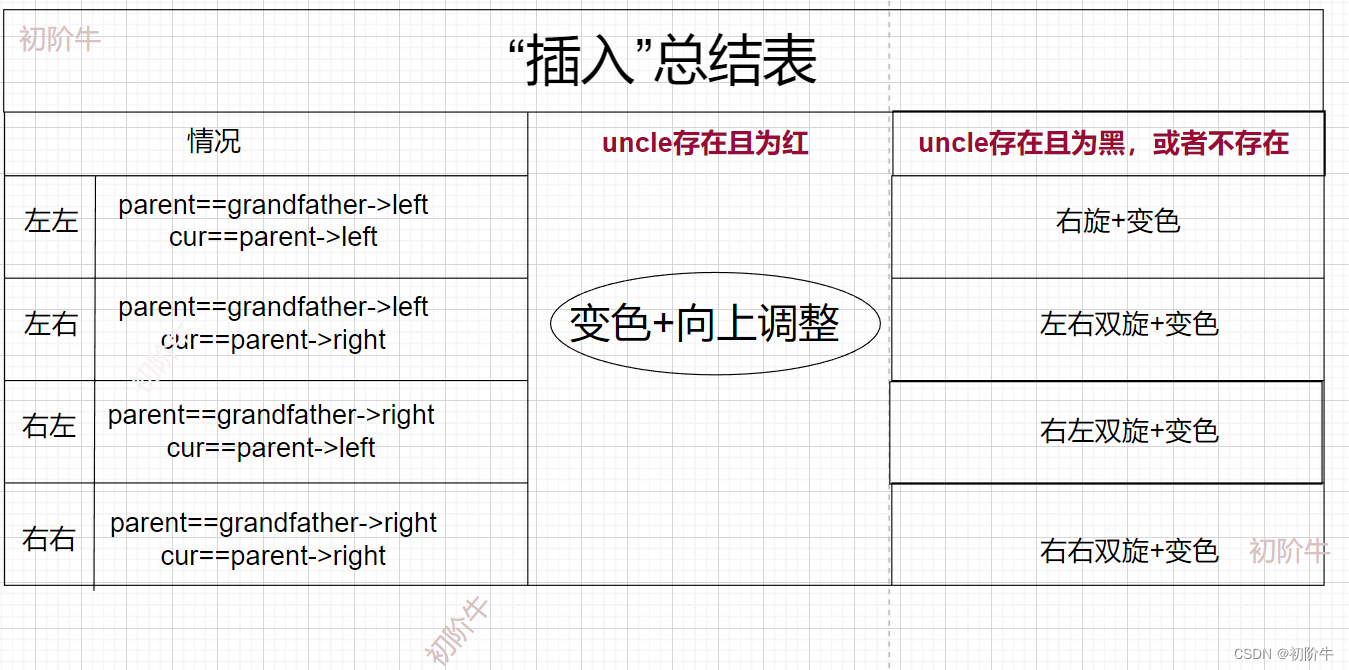
總代碼：

bool Insert(const T& kv) {if (_root == nullptr) {_root = new Node(kv);_root->_Col = BLACK;		//注意根節點一定是黑色的，默認構造的新節點是紅色的，所以這里要改一下。return true;}Node* cur = _root, * parent = nullptr;//尋找插入位置while (cur) {parent = cur;if (_root->_kv.first > kv.first) {cur = cur->_left;}else if (_root->_kv.first < kv.first) {cur = cur->_right;}else {return false;}}//判斷插入在左邊還是右邊cur = new Node(kv);if (kv.first < parent->_kv.first) {				//插入在左邊parent->_left = cur;}else {									//插入在右邊parent->_right = cur;}cur->_parent = parent;					//保證三叉鏈的關系//while (parent && parent->_Col == RED) {//爺爺結點Node* grandfather = parent->_parent;if (parent == grandfather->_left) {			//如果父親是爺爺的左孩子Node* uncle = grandfather->_right;		//那么叔叔就是爺爺的右孩子//叔叔存在且為紅if (uncle && uncle->_Col == RED) {//變色uncle->_Col=parent->_Col = BLACK;grandfather->_Col = RED;//繼續向上更新cur = grandfather;parent = grandfather->_parent;}else {									//叔叔不存在或者 存在且為黑if (cur == parent->_left) {			//			g//		p//cRotateR(grandfather);grandfather->_Col = RED;parent->_Col = BLACK;}else {//		g//	p//		cRotateL(parent);RotateR(grandfather);cur->_Col = BLACK;grandfather->_Col = RED;}break;	//此時最頂端的結點已經變成黑色了，不需要繼續向上更新了。}}else {		// 如果父親是爺爺的右孩子Node* uncle = grandfather->_left;		//那么叔叔就是爺爺的左孩子//叔叔存在且為紅if (uncle && uncle->_Col == RED) {//變色uncle->_Col = parent->_Col = BLACK;grandfather->_Col = RED;//繼續向上更新cur = grandfather;parent = grandfather->_parent;}else {									//叔叔不存在或者 存在且為黑if (cur == parent->_left) {//	g//		p//	c//注意旋轉時的傳參RotateR(parent);RotateL(grandfather);grandfather->_Col = RED;cur->_Col = BLACK;}else {//	g//		p//			cRotateL(grandfather);		//注意旋轉時的傳參parent->_Col = BLACK;grandfather->_Col = RED;}break;	//此時最頂端的結點已經變成黑色了，不需要繼續向上更新了。}}}_root->_Col = BLACK;		//最后根節點一定是黑的return true;}

2.22 最左側結點（LeftMost）

對于二叉搜索樹，如果我們按中序遍歷，則可以得到一個有序序列。
中序遍歷的首個結點： 最左側結點
中序遍歷的最后結點： 最右側結點

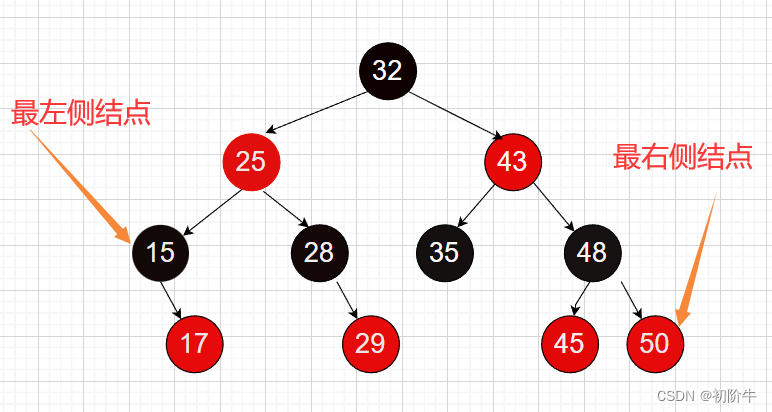
	// 獲取紅黑樹最左側節點template<class K, class V>typename RBTree<K, V>::Node* RBTree<K, V>::LeftMost() {Node* left_most = _root;while (left_most->left) {left_most = left_most->left;}return left_most;}

2.23 最右側結點（RightMost）

	// 獲取紅黑樹最右側節點template<class K, class V>typename RBTree<K, V>::Node* RBTree<K, V>::RightMost() {Node* right_most = _root;while (right_most->right) {right_most = right_most->left;}return right_most;}

2.24 檢測函數（次重點）

在實現紅黑樹時，也許我們會遇到各種問題，好不容易跑通代碼后，我們缺無法判斷自己實現的紅黑樹是否正確，是否符合紅黑樹的規則。

此時，我們可以設計一個檢測函數，檢測實現的紅黑樹是否平衡。

1. 空樹也是紅黑樹
2. 根節點必須是紅黑樹
3. 我們可以設置一個“基準值”，基準值為紅黑樹一條路徑中的黑色結點的個數。
4. 遍歷每條紅黑樹的路徑，判斷紅黑樹結點的個數，是否與基準值相等。
5. 除此之外，出現連續兩個紅色結點則返回false。

// 檢測紅黑樹是否為有效的紅黑樹，注意：其內部主要依靠_IsValidRBTRee函數檢測
template<class K, class V>
bool  RBTree<K, V>::IsValidRBTRee() {if (_root == nullptr)	//空樹也是紅黑樹return true;if (_root->_Col != BLACK)	//根節點必須是紅黑樹{return false;}// 基準值int pathBlack = 0;Node* cur = _root;while (cur){if (cur->_Col == BLACK)++pathBlack;cur = cur->_left;}_IsValidRBTRee(_root, 0, pathBlack);
}template<class K, class V>
bool RBTree<K, V>::_IsValidRBTRee(Node* pRoot, size_t blackCount, size_t pathBlack) {if (pRoot == nullptr){if (blackCount != pathBlack)		//一條路徑走到底，也就是走到葉子結點以后，判斷這條路徑上的黑色結點個數（blackCount）是否與 設定的黑色結點個數相同（pathBlack）return false;return true;}if (pRoot->_Col == BLACK){++blackCount;}if (pRoot->_Col == RED && pRoot->_parent && pRoot->_parent->_Col == RED){cout << _root->_kv.first << "出現連續紅色節點" << endl;return false;}//遞歸訪問左右子樹return _IsValidRBTRee(pRoot->_left, blackCount, pathBlack)&& _IsValidRBTRee(pRoot->_right, blackCount, pathBlack);
}

2.25 獲取根節點

	template<class K, class V>typename RBTree<K, V>::Node*& RBTree<K, V>::GetRoot() {return _root;}

2.25 獲取紅黑樹的高度

	template<class K, class V>int RBTree<K, V>::Height(){return Height(_root);}template<class K, class V>int RBTree<K, V>::Height(typename RBTree<K, V>::Node* root){if (root == nullptr)return 0;int leftHeight = Height(root->_left);	//計算左子樹的高度int rightHeight = Height(root->_right);	//計算右子樹的高度return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;}

2.26 find函數

template<class K, class T,>
typename RBTree<class K, class T, class Of_T>::Node* RBTree<class K, class T, class Of_T>::Find(const T& data) {Node* cur = _root;while (cur){if (data > cur->_data){cur = cur->_right;}else if (data < cur->_data){cur = cur->_left;}else return cur;}return nullptr;  // 找不到目標元素時返回nullptr
}

三、結語：

看完本篇文章，我們不難知道，對于插入操作，無論是紅黑樹還是avl樹，要維持對應的“平衡”，會進行沿路徑的更新，其中涉及大量的旋轉操作，而紅黑樹較于avl樹那種嚴格的高度差在-1到1之間，紅黑樹的平衡條件相對寬松，這也就大大減少了的為了維持平衡的大量旋轉操作，而且還能保證效率在log（N），這也就是為啥說紅黑樹較于avl樹更加優秀。
你贊同這個觀點嗎？

后續牛牛會模擬實現map和set，會在那篇文章封裝紅黑樹，對紅黑樹進行改造，增加迭代器等功能。幫助友友們更加深入理解map和set容器。