部分內容整理自張宇和網絡
序

題型分布:
| 題型 | 單題分值 | 題目數量 | 總分值 |
|---|---|---|---|
| 選擇題 | 5 | 3 | 15 |
| 填空題 | 5 | 1 | 5 |
| 解答題 | 12 | 1 | 12 |
*一道大題可能用到六部分所有知識
矩陣
性質
| k k k倍 | 和 | 乘積 | |
|---|---|---|---|
| 行列式 | ∣ k A ∣ = k n ∣ A ∣ |kA|=k^n|A| ∣kA∣=kn∣A∣ | ∣ A + B ∣ ≠ ∣ A ∣ + ∣ B ∣ |A+B|≠|A|+|B| ∣A+B∣=∣A∣+∣B∣ | ∣ A B ∣ = ∣ A ∣ ∣ B ∣ = ∣ B ∣ ∣ A ∣ |AB|=|A||B|=|B||A| ∣AB∣=∣A∣∣B∣=∣B∣∣A∣ |
| 轉置 | ( k A ) T = k A T (kA)^T=kA^T (kA)T=kAT | ( A + B ) T = A T + B T (A+B)^T=A^T+B^T (A+B)T=AT+BT | ( A B ) T = B T A T (AB)^T=B^TA^T (AB)T=BTAT |
| 逆 | ( k A ) ? 1 = 1 k A ? 1 (kA)^{-1}=\frac1kA^{-1} (kA)?1=k1?A?1 | A + B A+B A+B未必可逆,且 ( A + B ) ? 1 ≠ A ? 1 + B ? 1 (A+B)^{-1}≠A^{-1}+B^{-1} (A+B)?1=A?1+B?1 | ( A B ) ? 1 = B ? 1 A ? 1 (AB)^{-1}=B^{-1}A^{-1} (AB)?1=B?1A?1 |
| 伴隨 | ( k A ) ? = k n ? 1 A ? (kA)^*=k^{n-1}A^* (kA)?=kn?1A? | ( A + B ) ? ≠ A ? + B ? (A+B)^*≠ A^*+B^* (A+B)?=A?+B? | ( A B ) ? = B ? A ? (AB)^*=B^*A^* (AB)?=B?A? |
- 行列式的乘積等于乘積的行列式 ∣ A B ∣ = ∣ A ∣ ∣ B ∣ |AB|=|A||B| ∣AB∣=∣A∣∣B∣
- 轉置伴隨和逆 任意兩個運算順序可交換
基本運算
行列式
- ∏ i = 1 n λ i = ∣ A ∣ \prod\limits_{i=1}^n \lambda_i=|A| i=1∏n?λi?=∣A∣,所有特征值相乘結果等于行列式
- 矩陣可逆行列式不為零,矩陣不可逆行列式為零
- 矩陣逆矩陣的行列式等于原矩陣行列式的倒數
- r ( A A T ) = r ( A T A ) = r ( A ) r(AA^T)=r(A^TA)=r(A) r(AAT)=r(ATA)=r(A)
- 可逆乘可逆必可逆
求行列式
- 加邊法
- 伴隨矩陣行列式可用原矩陣行列式+特征值得出(見下方“伴隨矩陣的特征值”一節)
- 遞推法(通常是 n n n階行列式)
知乎 - 分塊矩陣行列式
圍繞矩陣 A A A可逆
- 矩陣若可逆,逆矩陣必唯一
- 逆矩陣特征值倒數
- ∣ A ? 1 ∣ = ∣ A ∣ ? 1 |A^{-1}|=|A|^{-1} ∣A?1∣=∣A∣?1,
- 證明矩陣 A A A可逆
- 求矩陣 A ? 1 A^{-1} A?1
求逆矩陣:
- 求 ∣ A ∣ ≠ 0 |A|≠0 ∣A∣=0
- 求 A ? A^* A?
- 代公式 A ? 1 = 1 ∣ A ∣ A ? A^{-1}=\frac{1}{|A|}A^* A?1=∣A∣1?A?
證矩陣 A A A可逆(利用性質):
- 可逆矩陣 r ( A ) = n r(A)=n r(A)=n(滿秩則可逆)
- 可逆矩陣 ∣ A ∣ ≠ 0 |A|\neq 0 ∣A∣=0(行列式值不為零則可逆)
- (按定義)存在 A B = B A = E AB=BA=E AB=BA=E則可逆
- 齊次線性方程AX=0,如果方程只有零解,則矩陣可逆,反之如果有無窮解,則矩陣不可逆
- 對于非齊次線性方程AX=b,如果方程只有一個特解,那么矩陣是可逆的;否則,如果有無窮解,矩陣是不可逆的。

秩
非零矩陣秩大于等于1,不滿秩的矩陣的行列式必然為0
- 對于矩陣 A m × n A_{m×n} Am×n?,必有 r ( A ) ≤ min ? { m , n } r(A)\le\min\{m,n\} r(A)≤min{m,n}
- r ( A B ) ≤ min ? { r ( A ) , r ( B ) } r(AB)\le\min\{r(A),r(B)\} r(AB)≤min{r(A),r(B)}
- 二級結論:對于矩陣 A m × n A_{m×n} Am×n?, r ( A ) = r ( A T A ) r(A)=r(A^TA) r(A)=r(ATA)
- 兩向量組被表出的秩不大
- 可逆矩陣滿秩(秩等于階數,行列式不為零)
- 若 A A A可逆,則 r ( A B ) = r ( B ) , r ( B A ) = r ( B ) r(AB)=r(B),r(BA)=r(B) r(AB)=r(B),r(BA)=r(B)
- 若 A A A是一個非零列向量, 則 r ( A A T ) = 1 r(AA^T)=1 r(AAT)=1
- 若 n n n階矩陣 A A A的某代數余子式 A i j ≠ 0 A_{ij}\neq 0 Aij?=0,意味著 r ( A ) ≥ n ? 1 r(A)\ge n-1 r(A)≥n?1(2020數學2第七題)
- A B = 0 AB=0 AB=0則 r ( A ) = r ( B ) ≤ 3 r(A)=r(B)\le 3 r(A)=r(B)≤3
r ( A ? ) = { n r ( A ) = n 1 r ( A ) = n ? 1 0 r ( A ) ≤ n ? 1 r(A^*)=\begin{cases} n \text{ \ \ \ \ \ }r(A)=n\\ 1\text{ \ \ \ \ \ }r(A)=n-1\\ 0\text{ \ \ \ \ \ }r(A)\le n-1\\ \end{cases} r(A?)=? ? ??n??????r(A)=n1??????r(A)=n?10??????r(A)≤n?1?
跡
矩陣 A A A的跡即對角線元素之和
t r ( A ) = ∑ i = 1 n a i i = a 11 + a 22 + a 33 + . . . + a n n tr(A)=\sum_{i=1}^na_{ii}=a_{11}+a_{22}+a_{33}+...+a_{nn} tr(A)=i=1∑n?aii?=a11?+a22?+a33?+...+ann?
性質/結論:
- r ( C ) = 1 r(C)=1 r(C)=1則 C n = [ t r ( C ) ] n ? 1 C C^n=[tr(C)]^{n-1}C Cn=[tr(C)]n?1C
性質:
- t r ( A ) = t r ( A T ) tr(A)=tr(A^T) tr(A)=tr(AT)
- t r ( A B ) = t r ( B A ) tr(AB)=tr(BA) tr(AB)=tr(BA)
- 循環性: t r ( A B C ) = t r ( B C A ) = t r ( C A B ) tr(ABC)=tr(BCA)=tr(CAB) tr(ABC)=tr(BCA)=tr(CAB)
- 相似矩陣跡相等,因為$$
- t r ( A + B ) + t r ( A ) + t r ( B ) tr(A+B)+tr(A)+tr(B) tr(A+B)+tr(A)+tr(B)
- 特征值之和等于矩陣的跡,特別是上三角矩陣, t r ( A ) = ∑ i = 1 n a i i = ∑ i = 1 n λ i i tr(A)=\sum_{i=1}^na_{ii}=\sum_{i=1}^n\lambda_{ii} tr(A)=∑i=1n?aii?=∑i=1n?λii?
關于5的解釋如下:
設 A A A、 B B B都是 n n n階矩陣,若有可逆矩陣 P P P,使 P ? 1 A P = B P^{-1}AP=B P?1AP=B則稱 A A A是 B B B的相似矩陣,或說 A A A和 B B B相似。
基于第三點,存在 t r ( A ) = t r ( P B P ? 1 ) = t r ( P P ? 1 B ) = t r ( B ) tr(A)=tr(PBP^{-1})=tr(PP^{-1}B)=tr(B) tr(A)=tr(PBP?1)=tr(PP?1B)=tr(B),可推知第五點
伴隨矩陣
伴隨矩陣的核心在于它的定義和其他推導的二級結論
A ? = ∣ A 11 A 21 . . . A n 1 A 12 A 22 . . . A n 2 ? ? ? A 1 n A 2 n . . . A n n ∣ A^*=\begin{vmatrix} A_{11} & A_{21} & ...& A_{n1} \\ A_{12} & A_{22} & ...& A_{n2} \\ \vdots & \vdots & &\vdots \\ A_{1n} & A_{2n} & ...& A_{nn} \end{vmatrix} A?= ?A11?A12??A1n??A21?A22??A2n??.........?An1?An2??Ann?? ?
其余二級結論如下:
- A A ? = A ? A = ∣ A ∣ E ? ∣ A A ? ∣ = ∣ ∣ A ∣ E ∣ ? ∣ A ∣ ∣ A ? ∣ = ∣ A ∣ n ? ∣ A ? ∣ = ∣ A ∣ n ? 1 AA^*=A^*A=|A|E\\\Rightarrow|AA^*|=||A|E|\\\Rightarrow|A||A^*|=|A|^n\\\Rightarrow|A^*|=|A|^{n-1} AA?=A?A=∣A∣E?∣AA?∣=∣∣A∣E∣?∣A∣∣A?∣=∣A∣n?∣A?∣=∣A∣n?1
- A ? = ∣ A ∣ A ? 1 A^*=|A|A^{-1} A?=∣A∣A?1
- A ? ( A ? ) ? = ∣ A ? ∣ E = ∣ A ∣ n ? 1 E ? ( A ? ) ? = ∣ A ∣ n ? 1 ( A ? ) ? 1 = ∣ A ∣ n ? 1 ( ∣ A ∣ A ? 1 ) ? 1 = ∣ A ∣ n ? 2 A A^*(A^*)^*=|A^*|E=|A|^{n-1}E\\\Rightarrow (A^*)^*=|A|^{n-1}(A^*)^{-1}=|A|^{n-1}(|A|A^{-1})^{-1}=|A|^{n-2}A A?(A?)?=∣A?∣E=∣A∣n?1E?(A?)?=∣A∣n?1(A?)?1=∣A∣n?1(∣A∣A?1)?1=∣A∣n?2A
- ∣ A ? ∣ = ∣ A ∣ n ? 1 |A^*|=|A|^{n-1} ∣A?∣=∣A∣n?1
當提到伴隨矩陣 A ? ≠ 0 A^*\neq 0 A?=0時,這意味著存在某個余子式 A i j ≠ 0 A_{ij}\neq 0 Aij?=0
? A \Rightarrow A ?A中有 n ? 1 n-1 n?1階子式不為零
? r ( A ) ≥ n ? 1 \Rightarrow r(A) \ge n-1 ?r(A)≥n?1
如果求多個余子式構成的式子(如 A 11 + A 22 + A 33 A_{11}+A_{22}+A_{33} A11?+A22?+A33?)就有可能用到伴隨矩陣作為輔助
等價
計算矩陣等價可以行列變換同時出現,但是解方程組時只可以進行行變換
矩陣等價時列向量組之間、行向量組之間可能不等價(也可能等價),但秩一定相等。向量組等價看下面“向量組”一節的“等價小節”
矩陣n次方
CSDN - 常見各種類型的矩陣n次方求法
知乎 - 線代——求矩陣的n次方方法總結
A A A、 B B B相似,則 A n A^n An、 B n B^n Bn相似
正交
正交矩陣行列式值為 ± 1 \pm1 ±1之一
向量組
線性相關/無關
首先明確這個在描述的是向量組,而且處理方法跟它是行向量或者列向量無關
線性無關 ? ∣ A ∣ ≠ 0 ? \Leftrightarrow|A|\neq 0 \Leftrightarrow ?∣A∣=0?滿秩 ? A x = 0 \Leftrightarrow Ax=0 ?Ax=0只有0解 ? A \Leftrightarrow A ?A可逆

即 α 1 \alpha_1 α1?、 α 2 . . . α n \alpha_2...\alpha_n α2?...αn?線性相關等價于
? A x = 0 \Leftrightarrow Ax=0 ?Ax=0有非零解
? r ( A ) < n \Leftrightarrow r(A)<n ?r(A)<n
- n n n個 n n n維向量 α 1 \alpha_1 α1?、 α 2 . . . α n \alpha_2...\alpha_n α2?...αn?相關 ? ∣ α 1 α 2 . . . α n ∣ = 0 \Leftrightarrow|\alpha_1\alpha_2...\alpha_n|=0 ?∣α1?α2?...αn?∣=0
- n + 1 n+1 n+1個 n n n維向量必線性相關
- 兩向量組被表出的秩不大(若不能被表出,秩之間無必然大小關系)
- 不成比例,線性無關
- 若 A = [ α 1 α 2 . . . α n ] A=[\alpha_1\alpha_2...\alpha_n] A=[α1?α2?...αn?]相似于B,若B線性無關,則A線性無關
證明 α 1 \alpha_1 α1?、 α 2 . . . α n \alpha_2...\alpha_n α2?...αn?線性無關的方法:
- 定義法(見上面的流程圖)(重組或乘)
- 證明秩 r ( α 1 α 2 . . . α n ) = n r(\alpha_1\alpha_2...\alpha_n)=n r(α1?α2?...αn?)=n
- 反證法
處理向量組 I I I能由向量組 I I II II線性表出,而反過來不能的問題
關于被表出的秩不大的特例:若 α 1 \alpha_1 α1?、 α 2 . . . α n \alpha_2...\alpha_n α2?...αn?可用 β 1 β 2 . . . β n \beta_1\beta_2...\beta_n β1?β2?...βn?表出,但 β 1 β 2 . . . β n \beta_1\beta_2...\beta_n β1?β2?...βn?不可用 α 1 \alpha_1 α1?、 α 2 . . . α n \alpha_2...\alpha_n α2?...αn?表出,則 r ( α 1 r(\alpha_1 r(α1?、 α 2 . . . α n ) < r ( β 1 β 2 . . . β n ) \alpha_2...\alpha_n)<r(\beta_1\beta_2...\beta_n) α2?...αn?)<r(β1?β2?...βn?)
若向量組 I I I能由向量組 I I II II線性表出,且 r ( I ) = r ( I I ) r(I)=r(II) r(I)=r(II),則兩向量組等價
若 α 1 \alpha_1 α1?、 α 2 . . . α n \alpha_2...\alpha_n α2?...αn?可用 β 1 β 2 . . . β n \beta_1\beta_2...\beta_n β1?β2?...βn?表出,即 r ( α 1 r(\alpha_1 r(α1?、 α 2 . . . α n ) ≤ r ( β 1 β 2 . . . β n ) \alpha_2...\alpha_n)\le r(\beta_1\beta_2...\beta_n) α2?...αn?)≤r(β1?β2?...βn?)
但另一方面由于向量組等價即可以互相表出,與前提“ β 1 β 2 . . . β n \beta_1\beta_2...\beta_n β1?β2?...βn?不可用 α 1 \alpha_1 α1?、 α 2 . . . α n \alpha_2...\alpha_n α2?...αn?表出”矛盾,則兩秩必不可能相等,故 r ( α 1 r(\alpha_1 r(α1?、 α 2 . . . α n ) < r ( β 1 β 2 . . . β n ) \alpha_2...\alpha_n)<r(\beta_1\beta_2...\beta_n) α2?...αn?)<r(β1?β2?...βn?)
線性表出
若向量 β \beta β可以由 α 1 α 2 . . . α n \alpha_1\alpha_2...\alpha_n α1?α2?...αn?線性表出
? ? \Leftrightarrow \exist ??實數 k 1 k 2 . . . k n k_1k_2...k_n k1?k2?...kn?使 k 1 α + k 2 α + . . . + a n α = β k_1\alpha +k_2\alpha +...+a_n\alpha=\beta k1?α+k2?α+...+an?α=β
? ? \Leftrightarrow \exist ??實數 k 1 k 2 . . . k n k_1k_2...k_n k1?k2?...kn?使
( α 1 α 2 . . . α n ) [ k 1 k 2 ? k n ] = β (\alpha_1\alpha_2...\alpha_n)\begin{bmatrix} k_1 \\ k_2 \\ \vdots\\ k_n \end{bmatrix}=\beta (α1?α2?...αn?) ?k1?k2??kn?? ?=β
? \Leftrightarrow ?下面的方程組有解(方程組有解問題可以使用增廣矩陣解方程組)
( α 1 α 2 . . . α n ) [ k 1 k 2 ? k n ] = β (\alpha_1\alpha_2...\alpha_n)\begin{bmatrix} k_1 \\ k_2 \\ \vdots\\ k_n \end{bmatrix}=\beta (α1?α2?...αn?) ?k1?k2??kn?? ?=β
? \Leftrightarrow ?秩 r ( α 1 α 2 . . . α n ) = r ( α 1 α 2 . . . α n β ) r(\alpha_1\alpha_2...\alpha_n)=r(\alpha_1\alpha_2...\alpha_n\beta) r(α1?α2?...αn?)=r(α1?α2?...αn?β)
此處引用知乎用戶的(來源見水印)的一張圖

- 研究秩相等與否
- 反證法(根據表達式構造矛盾)
- 若 k s ≠ 0 k_s\neq 0 ks?=0(根據題意選擇)證明
表示法不唯一
若 β \beta β可由 α 1 α 2 . . . α n \alpha_1\alpha_2...\alpha_n α1?α2?...αn?線性表示,且向量都是 n n n維列向量,則方程組有 A x = β Ax=\beta Ax=β有無窮多解,即應求得 r ( A ) = r ( A ∣ B ) < n r(A)=r(A|B)<n r(A)=r(A∣B)<n成立
等價
兩個向量組能互相線性表出就稱這兩個向量組等價
- 向量組等價不要求每個組向量個數相同,只要維數一樣即可
- 計算/判斷依據:向量組 I I I和 I I II II存在關系 r ( I ) = r ( I I ) = r ( I ∣ I I ) r(I)=r(II)=r(I|II) r(I)=r(II)=r(I∣II)即三秩相同
- 向量組 I I I和 I I II II等價則記為 ( I ) ≌ ( I I ) (I)≌(II) (I)≌(II)
- 向量組和它的極大線性無關組是等價向量組
向量空間
結合3D圖形領域常說的世界空間坐標和物體局部坐標比較好理解
基變換公式則是
線性方程組
我把它寫在另一篇文章里了:線性方程組的求解問題
- 齊次方程組有無窮多解則 r ( A ) < n r(A) < n r(A)<n,畢竟這樣才能有 n ? r ( A ) n-r(A) n?r(A)個自由量,自由量含 k k k,而 k k k任意取值,那自然就是無窮多解
- A x = 0 Ax=0 Ax=0只有0解 ? r ( A ) = n \Leftrightarrow r(A)=n ?r(A)=n
- A x = b Ax=b Ax=b有唯一解 ? r ( A ) = r ( A  ̄ ) = n \Leftrightarrow r(A)=r(\overline{A})=n ?r(A)=r(A)=n
- 但是 A x = 0 Ax=0 Ax=0只有0解不能推知 A x = b Ax=b Ax=b有唯一解
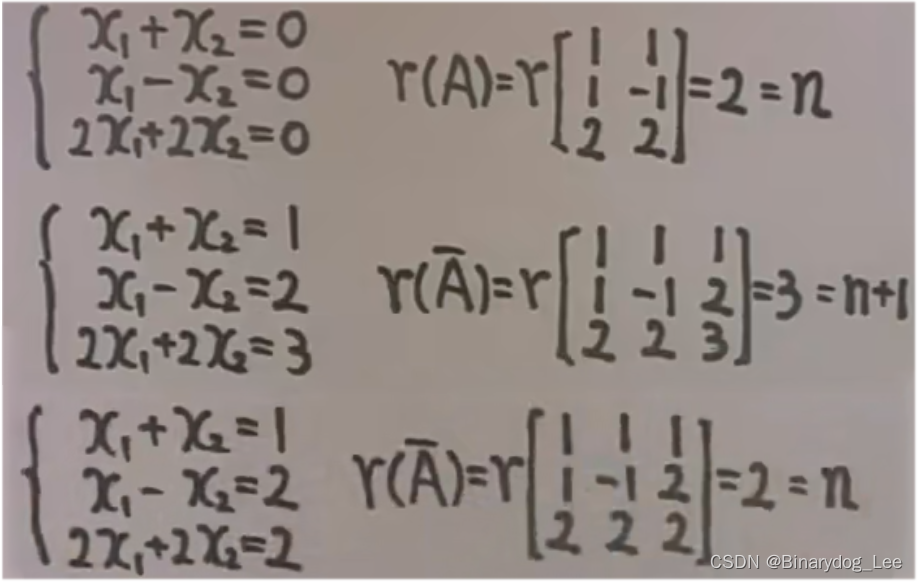
公共解問題
開頭先說“因為方程組 ( 1 ) (1) (1)與 ( 2 ) (2) (2)的公共解即為聯立方程組 ( 3 ) (3) (3)(這里要具體寫出來聯立的方程組內容)的解”,就有兩分
對聯立方程組 ( 3 ) (3) (3)做初等行變換有 A  ̄ = . . . \overline A=... A=...
若參數 a = . . . a=... a=...則有解,此時…(按常規解法進行就可以了)
若給出的不是兩個線性方程組,而是一個線性方程組和另一個方程組的解,則

同解問題
同解問題的本質是行變換(右乘矩陣)解不變
- 若 A A A、 B B B同解 ? r ( A ) = r ( B ) \Rightarrow r(A)=r(B) ?r(A)=r(B)(不可反推)
- 常用 A A A的解帶入 B B B的式子定 B B B系數矩陣中的未知數,但是定出來之后還是要化簡和 A A A比較一下的,因為存在 B B B的解包含 A A A的解的情況,此時 B B B包含一些獨有的解。
- A T A x = 0 A^TAx=0 ATAx=0和 A x = 0 Ax=0 Ax=0同解

特征值與特征向量
特征值和特征向量不是一對一的關系,一個特征值對應的特征向量可能構成一個空間(解空間)
如 α 1 α 2 \alpha_1\alpha_2 α1?α2?是矩陣 A A A關于特征值 λ \lambda λ的特征向量,則 k 1 α 1 + k 2 α 2 k_1\alpha_1+k_2\alpha_2 k1?α1?+k2?α2?(非0時)仍是 A A A關于 λ \lambda λ的特征向量
如 α 1 α 2 \alpha_1\alpha_2 α1?α2?是矩陣 A A A不同特征值的特征向量,則 k 1 α 1 + k 2 α 2 k_1\alpha_1+k_2\alpha_2 k1?α1?+k2?α2?不是 A A A的特征向量
- ∏ i = 1 n λ i = ∣ A ∣ \prod\limits_{i=1}^n \lambda_i=|A| i=1∏n?λi?=∣A∣,所有特征值相乘結果等于行列式
- ∑ i = 1 n λ i = ∑ i = 1 n a i i = t r ( A ) \sum\limits_{i=1}^n\lambda_i=\sum\limits_{i=1}^n a_{ii}=tr(A) i=1∑n?λi?=i=1∑n?aii?=tr(A)
- k k k階矩陣最多會有 k k k個特征值
- 不同特征值對應的特征向量是線性無關的
- 相同的特征值對應的特征向量可能線性無關也可能線性相關
- 能夠相似對角化和是否不含重根沒有必然聯系
- 上三角矩陣主對角線元素就是特征值,若均不同,可立即推出能對角化
對于相同的特征值(重根),對應的特征向量可能構成一個解空間,但是這個n維的解空間內只有 n n n個向量線性無關,其余向量均可用這 n n n個線性無關的向量表示,所以可能線性無關也可能線性相關。
故也有結論:若 ξ 1 \xi_1 ξ1?、 ξ 2 \xi_2 ξ2?是屬于同一個特征值 λ \lambda λ的特征向量時, k 1 ξ 1 + k 2 ξ 2 k_1\xi_1+k_2\xi_2 k1?ξ1?+k2?ξ2?也是屬于特征值 λ \lambda λ的特征向量
相似對角化與重根:對于 n n n階矩陣 A A A的各個特征值中,對于各重根,若滿足 n ? r ( λ i E ? A ) = n i n-r(\lambda_i E-A)=n_i n?r(λi?E?A)=ni?,其中 λ i \lambda_i λi?是 n i n_i ni?重根。此時可以相似對角化,即這個 s s s重根對應能有 s s s個線性無關的特征向量
伴隨矩陣特征值

秩為1的矩陣特征值的結論推導
凡是 n n n階方陣 A A A秩為1,其特征值構成為 n ? 1 n-1 n?1個0,和一個 t r ( A ) tr(A) tr(A)
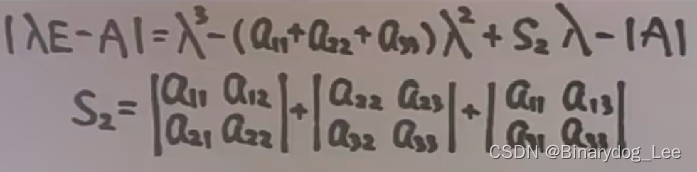
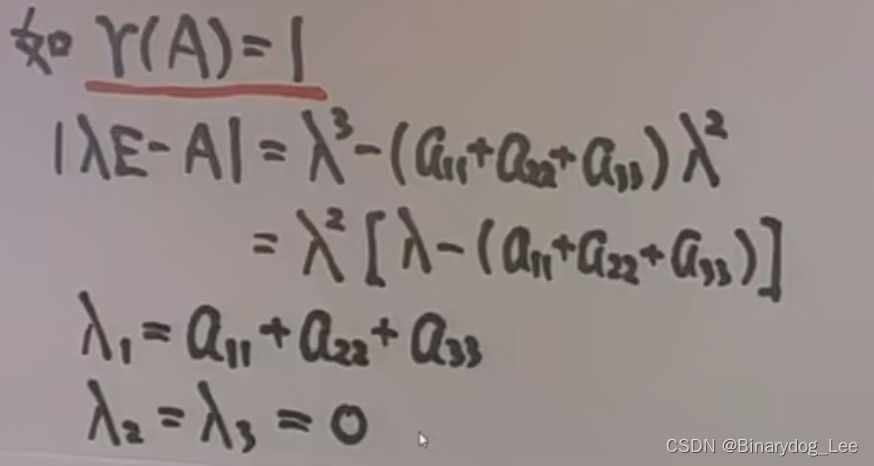
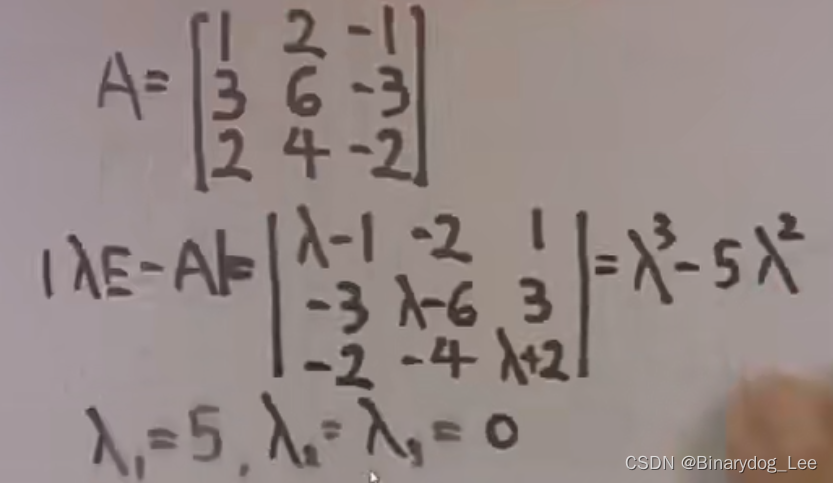

求特征值、特征向量
- A α = λ α ( α ≠ 0 ) A\alpha=\lambda \alpha (\alpha \neq 0) Aα=λα(α=0)
- ∣ λ E ? A ∣ = 0 , ( λ i E ? A ) x = 0 |\lambda E - A|=0,(\lambda_i E-A)x=0 ∣λE?A∣=0,(λi?E?A)x=0
- 如 P ? 1 A P = B P^{-1}AP=B P?1AP=B
- 若 A α = λ α A\alpha=\lambda \alpha Aα=λα則 B ( P ? 1 α ) = λ ( P ? 1 α ) B(P^{-1}\alpha)=\lambda(P^{-1}\alpha) B(P?1α)=λ(P?1α)
- 若 B α = λ α B\alpha=\lambda \alpha Bα=λα則 A ( P α ) = λ ( P α ) A(P \alpha)=\lambda(P \alpha) A(Pα)=λ(Pα)
關于2的注:由特征值 λ \lambda λ解出特征向量 ξ \xi ξ,實際上是在解線性方程組 ( λ E ? A ) ξ = 0 (\lambda E-A)\xi=0 (λE?A)ξ=0,具體操作與上一節線性方程組內容一致,參閱即可。
求解線性方程組最后解要加上系數 k k k,但是要注明 k ≠ 0 k\neq 0 k=0,因為特征向量不為零
求特征值要先帶 ∣ λ E ? A ∣ = 0 |\lambda E - A|=0 ∣λE?A∣=0再化簡,不能先化簡再代
矩陣相似
設 A A A、 B B B都是 n n n階矩陣,若有可逆的 n n n階矩陣 P P P,使 P ? 1 A P = B P^{-1}AP=B P?1AP=B則稱 A A A是 B B B的相似矩陣,或說 A A A和 B B B相似,記為 A ~ B A\sim B A~B。
- [反身性] A ~ A A\sim A A~A
- [對稱性]若 A ~ B A\sim B A~B,則 B ~ A B\sim A B~A
- [傳遞性]若 A ~ B A\sim B A~B, B ~ C B\sim C B~C,則 A ~ C A\sim C A~C
相似矩陣的性質:
若有 P ? 1 A P = B P^{-1}AP=B P?1AP=B,則 A A A和 B B B相似,可推知:
- A與B行列式相等 ∣ A ∣ = ∣ B ∣ |A|=|B| ∣A∣=∣B∣
- A與B具有相同的可逆性,即若 A A A可逆,則有 A ? 1 A^{-1} A?1與 B ? 1 B^{-1} B?1相似
- A與B具有相同的秩、特征值多項式、特征值和跡
- A n ~ B n A^n \sim B^n An~Bn
由 A A A和 B B B相似還可推知 A + k E ~ B + k E A+kE \sim B+kE A+kE~B+kE,進一步類似地:
- ∣ A + k E ∣ = ∣ B + k E ∣ |A+kE |=| B+kE| ∣A+kE∣=∣B+kE∣
- r ( A + k E ) = r ( B + k E ) r(A+kE)=r(B+kE) r(A+kE)=r(B+kE)
若 A ~ B A \sim B A~B則 A A A是否能對角相似的問題可以轉化為 B B B能否對角相似的問題
※相似有這些性質,但有這些性質的未必相似
- 實對稱矩陣有相同的特征值必相似
- 特征值是重根得具體討論是否相似(見下一節)
A A A和 B B B相似
- 矩陣 λ E ? A \lambda E- A λE?A和 λ E ? B \lambda E- B λE?B未必相等
- A A A和 B B B未必相似于同一個對角矩陣
- A A A和 B B B未必有相同的特征向量
矩陣的相似對角化
大題里面總要有某個題的中間步驟用到相似對角化
若對于 n n n階矩陣 A A A
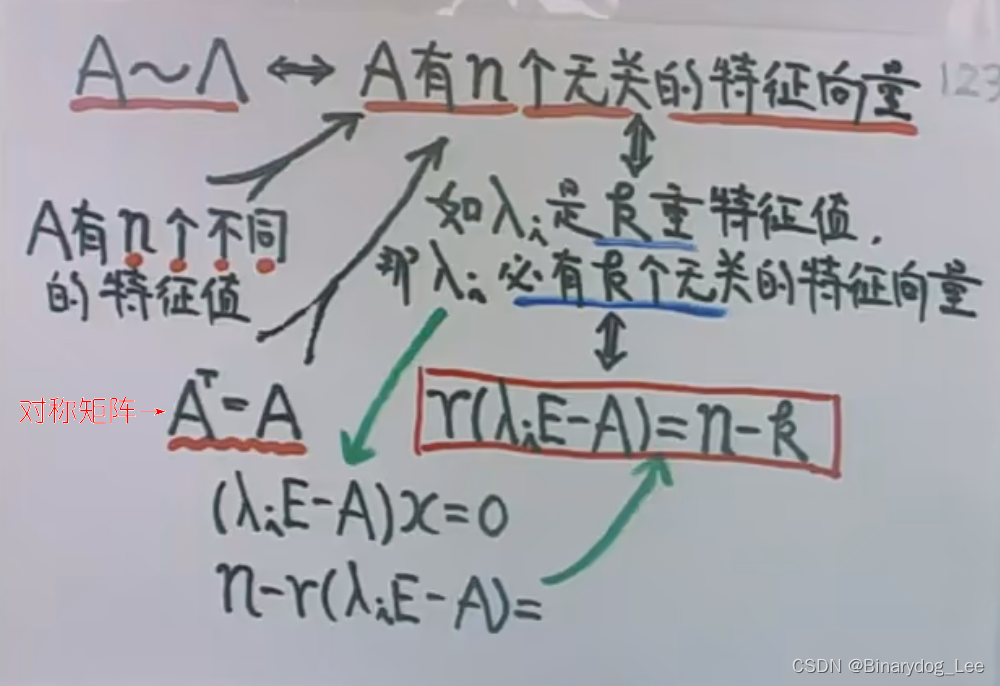
- A ~ Λ ? A A\sim \Lambda \Leftrightarrow A A~Λ?A有 n n n個線性無關的特征向量 ξ \xi ξ
- A ~ Λ ? n i = n ? r ( λ i E ? A ) A\sim \Lambda \Leftrightarrow n_i=n-r(\lambda_i E-A) A~Λ?ni?=n?r(λi?E?A),其中 λ i \lambda_i λi?是 n i n_i ni?重根
- A A A有 n n n個不同的特征值 λ ? A ~ Λ \lambda \Rightarrow A \sim \Lambda λ?A~Λ
- A A A是實對稱矩陣 ? A ~ Λ \Rightarrow A \sim \Lambda ?A~Λ
前兩個是充要條件,后兩個是充分條件


相似對角化的意義
參閱知乎文章:理解矩陣的相似對角化
如果矩陣 A n × n A_{n×n} An×n?能夠相似對角化,則會有 P ? 1 A P = Λ P^{-1}AP=\Lambda P?1AP=Λ,其中 P P P稱為相似變換矩陣,且 P P P不唯一。因為P是由 n n n個線性無關的特征向量構成的(由于解出特征向量是一個解線性方程組的問題,其解通常構成一個空間,而在空間內選取一組線性無關的向量有很多種選法),出于方便使用, P P P往往會選擇為正交矩陣。
相似對角化的意義就是坐標系的變換。作用是通過對坐標系的變換,選取不同的基,使某些運算簡單些。(此處就對應了常見題型“由特征值、特征向量反求 A A A”)
如求 B n B^n Bn,若有 B n = P ? 1 Λ n P B^n=P^{-1}\Lambda^nP Bn=P?1ΛnP,此處的 Λ n \Lambda^n Λn計算肯定比 B n B^n Bn的計算方便
A P = A ( γ 1 γ 2 γ 3 ) = ( γ 1 γ 2 γ 3 ) [ a 1 a 2 a 3 ] ? ( A γ 1 ,? A γ 2 ,? A γ 3 ) = ( a 1 γ 1 ,? a 2 γ 2 ,? a 3 γ 3 ) AP=A(\gamma_1\gamma_2\gamma_3)=(\gamma_1\gamma_2\gamma_3)\begin{bmatrix} a_1 & & \\ & a_2 & \\ & & a_3 \end{bmatrix}\\\Leftrightarrow(A\gamma_1\text{, }A\gamma_2\text{, }A\gamma_3)=(a_1 \gamma_1\text{, }a_2\gamma_2\text{, }a_3\gamma_3) AP=A(γ1?γ2?γ3?)=(γ1?γ2?γ3?) ?a1??a2??a3?? ??(Aγ1?,?Aγ2?,?Aγ3?)=(a1?γ1?,?a2?γ2?,?a3?γ3?)
顯然對角矩陣的值是 A A A的特征值, P P P的列向量是 A A A的特征向量
若 P ? 1 A P ~ B ≠ Λ P^{-1}AP \sim B \neq \Lambda P?1AP~B=Λ,則此處的 P P P 不是 A A Ad的特征向量
判斷相似
考研討論的矩陣一般都是實矩陣
- 實對稱矩陣必可相似于對角矩陣
- 特征值不重復的矩陣必可相似于對角矩陣
- 特征值有重根且 k i = n ? r ( λ i E ? A ) k_i = n-r(\lambda_i E-A) ki?=n?r(λi?E?A)的必可相似于對角矩陣,其中 k i k_i ki?是重根 λ i \lambda_i λi?的個數
藉由傳遞性:若 A ~ B A\sim B A~B, B ~ C B\sim C B~C,則 A ~ C A\sim C A~C,證明矩陣 A A A和 C C C相似實際上需要找到中間的矩陣(通常是對角矩陣) Λ Λ Λ,證出 A ~ Λ A\simΛ A~Λ和 C ~ Λ C\sim Λ C~Λ
判斷不相似(相似的4個必要條件)
- ∣ A ∣ ≠ ∣ B ∣ |A|\neq |B| ∣A∣=∣B∣
- r ( A ) ≠ r ( B ) r(A)\neq r(B) r(A)=r(B)
- λ A ≠ λ B \lambda_A\neq \lambda_B λA?=λB?
- ∑ a i i ≠ ∑ b i i \sum a_{ii} \neq \sum b_{ii} ∑aii?=∑bii?
- A ~ Λ A\sim \Lambda A~Λ但 B B B不可相似對角化
- A + k E ? B + k E A+kE \nsim B+kE A+kE?B+kE則 A A A和 B B B不相似
判斷相似
- 相似于同一對角矩陣的兩矩陣相似(即上面的傳遞性)
- 實對稱矩陣相似 ? \Leftrightarrow ?兩矩陣特征值一樣
求可逆矩陣 P P P使 P ? 1 A P ~ Λ P^{-1}AP \sim \Lambda P?1AP~Λ
P P P是 A A A的特征向量
- 預處理
- 求特征值( ∣ λ E ? A ∣ = 0 |\lambda E - A|=0 ∣λE?A∣=0得到 λ 1 \lambda_1 λ1?、 λ 2 \lambda_2 λ2?、 λ 3 \lambda_3 λ3?)
- 求特征向量
- 構造可逆 P = [ α 1 α 2 α 3 ] P=[\alpha_1 \alpha_2 \alpha_3] P=[α1?α2?α3?]
P ? 1 A P = Λ = [ λ 1 λ 2 λ 3 ] P^{-1}AP=\Lambda = \begin{bmatrix} \lambda_1 & & \\ & \lambda_2 & \\ & & \lambda_3 \end{bmatrix} P?1AP=Λ= ?λ1??λ2??λ3?? ?
顯然若有重根就得按解線性方程組的方法算出解空間內的一組( k k k個)線性無關的向量作為 k k k重根的特征向量 α 1 ? α k \alpha_1\cdots\alpha_k α1??αk?,加上其余的特征向量構成 P = [ α 1 α 2 ? α n ] P=[\alpha_1 \alpha_2 \cdots\alpha_n] P=[α1?α2??αn?]
求正交矩陣 Q Q Q使 Q ? 1 A Q ~ Λ Q^{-1}AQ \sim \Lambda Q?1AQ~Λ
關鍵是注意單位化
- 預處理
- 求特征值( ∣ λ E ? A ∣ = 0 |\lambda E - A|=0 ∣λE?A∣=0得到 λ 1 \lambda_1 λ1?、 λ 2 \lambda_2 λ2?、 λ 3 \lambda_3 λ3?)
- 求特征向量
- 改造特征向量
- 若 λ i ≠ λ j \lambda_i \neq \lambda _j λi?=λj? 只需單位化
- 若 λ i = λ j \lambda_i =\lambda _j λi?=λj?(特征值有重根)先施密特正交化(如果不正交的話)再單位化
特征向量內積不得零就得正交化
施密特正交化
知乎 - 如何理解施密特正交化
知識串聯

說明:
- 得到 n n n階矩陣 A A A
- 求出 λ \lambda λ和 ξ \xi ξ(有多個)
- 確定 ξ 1 ξ 2 . . . ξ n \xi_1 \text{ } \xi_2 ... \xi_n ξ1??ξ2?...ξn?是 n n n個線性無關向量
- 構造 P = ( ξ 1 ξ 2 . . . ξ n ) P=(\xi_1 \text{ } \xi_2 ... \xi_n) P=(ξ1??ξ2?...ξn?)
- 確定 P P P可逆
- 存在下式,且構成下式的 λ \lambda λ均為 A A A的特征值
P ? 1 A P = ∣ λ 1 λ 2 ? λ n ∣ P^{-1}AP=\begin{vmatrix} \lambda_1 & & &\\ & \lambda_2 & &\\ & & \ddots & \\ & & & \lambda_n \end{vmatrix} P?1AP= ?λ1??λ2????λn?? ?
對角線上的 λ \lambda λ的順序是1、2…n,是因為構成 P P P的向量下標也是這個順序,這倆得保持一致
構成對角化矩陣的元素就是原矩陣 A A A的特征值
二次型
通過? x = P y 將? x T A x 變換為? y T P T A P y 通過 \text{ }x=Py \text{ }將 \text{ }x^TAx \text{ }變換為 \text{ }y^TP^{T}APy 通過?x=Py?將?xTAx?變換為?yTPTAPy
顯然在原先的 x T A x x^TAx xTAx中參數(變量/坐標軸)是 x x x,系數矩陣的 A A A,而變化之后參數是 y y y,系數矩陣是 P T A P P^{T}AP PTAP,如果 P T A P P^{T}AP PTAP是對角矩陣,則無交叉項(變成了標準型)
- P ? 1 A P = Λ P^{-1}AP= \Lambda P?1AP=Λ:相似對角化(上一節特征值的東西)
- P T A P = Λ P^{T}AP= \Lambda PTAP=Λ:合同對角化
相似和合同本無必然聯系,但是在實對稱矩陣下相似必合同,在實對稱矩陣下合同的充要條件的
二次齊次多項式(二次型)可以寫為矩陣形式 f ( x ) = x T A x f(x)=x^TAx f(x)=xTAx,其中 A = A T A=A^T A=AT,是個實對稱矩陣,叫做系數矩陣。二次型寫成矩陣的形式有很多種方式,選用實對稱矩陣是因為方便后續計算,利于后面研究問題。
- 系數矩陣 A A A的秩就是二次型的秩
- 可逆線性變換不會改變二次型的秩
- 正交變換的意義是對坐標軸進行旋轉,但是不會導致圖形的扭曲
發現像坐標變換的先看行列式,若行列式為零就不是坐標變換
x T ( A + B ) x = x T A x + x T B x x^T(A+B)x=x^TAx+x^TBx xT(A+B)x=xTAx+xTBx
合同
合同的前提是在討論實對稱矩陣
f ( x ) = x T A x f(x)=x^TAx f(x)=xTAx, g ( y ) = y T B y g(y)=y^TBy g(y)=yTBy,若有矩陣 C C C使得 x = C y x=Cy x=Cy(亦即 C T A C = B C^TAC=B CTAC=B),則 A A A與 B B B合同,記為 A ? B A \simeq B A?B。 x = C y x=Cy x=Cy即原坐標系與新坐標系下的坐標替換公式,
閱讀:矩陣合同的本質是什么,在坐標系或者基中? - 馬同學的回答 - 知乎
做合同變換的意義是使二次型沒有交叉項(即只有平方項,并且這種形式稱為標準型)。而標準型的系數矩陣恰恰只有對角線有元素,其他位置為0,這和“矩陣相似對角化”這一操作得到的結果不謀而合,所以相似對角化能作為矩陣化為標準型用到的手段。
二次型化為標準型的三種方法:
- 配方法
- 正交變換
- 合同變換
詳細可參閱:
- 請問求二次型的標準型的三種方法? - yfli-math的回答 - 知乎
- 正交變換最強總結筆記,解決每一個考研線代人的理解難關 - 煜神學長的文章 - 知乎
- kaysen學長:配方法化二次型為標準型通俗講解!理解門檻降為0,不再配出一地雞毛!
判斷合同的方法:
- 兩個實對稱矩陣合同的充要條件是它們的正負慣性指數相同
- 實對稱矩陣相似必然合同
- 合同矩陣必為等價矩陣,等價矩陣未必為合同矩陣
慣性定理
同一個二次型通過不同的可逆變換,所得的不同標準形,系數為正的項數(正慣性指數)和系數為負的項數(負慣性指數)相同。
依靠慣性定理比較兩個二次型是否能互相轉換
- 使用特征值求正負慣性指數的數目
- 配方法求正負慣性指數的數目
欲求正負慣性指數需要先求標準型,即由 ∣ λ E ? A ∣ = 0 |\lambda E-A|=0 ∣λE?A∣=0算特征值看正負項數目即可
配方法
配方法得到一個新的式子(下為例子)
( x 1 + x 2 + 2 x 3 ) 2 + ( x 2 + 5 x 3 ) 2 + x 3 2 ? y = [ 1 1 2 0 1 5 0 0 1 ] x ? y = P x ? x = P ? 1 y (x_1+x_2+2x_3)^2+(x_2+5x_3)^2+x_3^2\Rightarrow y=\begin{bmatrix}1 &1&2\\0&1&5\\0&0&1\end{bmatrix}x\Leftrightarrow y=Px\Leftrightarrow x = P^{-1}y (x1?+x2?+2x3?)2+(x2?+5x3?)2+x32??y= ?100?110?251? ?x?y=Px?x=P?1y
那個 P ? 1 P^{-1} P?1才是坐標變換
把二次型A化為另一個非標準型的二次型B
正交變換化為標準型
經過坐標變換,二次型矩陣一定合同
經過正交變換,二次型矩陣不僅合同而且相似
求二次型 x T A x x^TAx xTAx在正交變換下的標準型就也就是求二次型矩陣 A A A的特征值
對于任給的 n n n元二次型 f ( x ) = x T A x f(x)=x^TAx f(x)=xTAx,總有正交變換 x = Q y x=Qy x=Qy把 f ( x ) f(x) f(x)化為標準型 g ( y ) = λ 1 y 1 2 + λ 2 y 2 2 + . . . + λ n y n 2 g(y)=\lambda_1y_1^2+\lambda_2y_2^2+...+\lambda_ny_n^2 g(y)=λ1?y12?+λ2?y22?+...+λn?yn2?,其中 λ 1 , λ 2 . . . λ n \lambda_1,\lambda_2...\lambda_n λ1?,λ2?...λn?是 A A A的特征值
若 Q Q Q是正交矩陣, x = Q y x=Qy x=Qy就是正交變換。
實際上就是對二次型的系數矩陣 A A A求相似對角化的矩陣 Λ \Lambda Λ,那就是標準型,然后對應的坐標變換 x = Q y x=Qy x=Qy的 Q Q Q由 A A A的特征值構成,并且得正交化和單位化
步驟:
- 根據二次型寫出 A A A
- 求 A A A的 λ \lambda λ和 ξ \xi ξ
- ξ 1 . . . ξ n \xi_1...\xi_n ξ1?...ξn?正交化&單位化為 η 1 . . . η n \eta_1...\eta_n η1?...ηn?,則正交矩陣 Q = ( η 1 . . . η n ) Q=(\eta_1...\eta_n) Q=(η1?...ηn?),且有性質 Q T = Q ? 1 Q^T=Q^{-1} QT=Q?1, Q ? 1 A Q = Λ Q^{-1}AQ=\Lambda Q?1AQ=Λ
- 令 x = Q y x=Qy x=Qy則 f ( x ) = x T A x = ( Q Y ) T A Q Y = Y T Q T A Q Y = Y Λ Y f(x)=x^TAx=(QY)^TAQY=Y^TQ^TAQY=Y\Lambda Y f(x)=xTAx=(QY)TAQY=YTQTAQY=YΛY
顯然,這里是用正交矩陣 Q Q Q把 A A A相似對角化
標準型項數的關系
標準型/規范性項數即原先系數矩陣的秩(經過坐標變換秩不變)
顯然在三維空間下,若化為的標準型為 y 1 + y 2 y_1+y_2 y1?+y2?(兩項),則原二次型秩為2,顯然必有其中一個特征值 λ = 0 \lambda=0 λ=0
規范型
得到規范性的前提是得到標準型,對標準型做伸縮變換即可。標準型的求法參見上方內容。
規范型只和平方項系數正負有關,和系數大小無關

倘若給出的不是標準型(即含有交叉項),則可考慮配方法。若配方法過于復雜,則應當對原二次型的系數矩陣 A A A 求特征值,根據特征值的正負數目(正負慣性指數)確定規范型的正負
正定
前提有 A = A T A=A^T A=AT(即正定隱含的條件就是矩陣是對稱矩陣)
- A A A正定, A T A^T AT必正定(因為實對稱矩陣 A = A T A=A^T A=AT)
- A A A正定 ? A ? 1 \Leftrightarrow A^{-1} ?A?1正定(這個是正反都成立的)
- A A A正定 ? A ? \Rightarrow A^* ?A?正定(這個是沒法倒推的)
處理步驟:
- 寫出二次型的系數矩陣(如果需要)
- 檢查是否對稱
- 證明正定
證明正定的方法:
- 定義法
- 特征值大于0(充要條件)
- 正慣性指數=n(和單位矩陣合同 A = C T E C = C T C A=C^TEC=C^TC A=CTEC=CTC)
正定的必要條件:平方項系數大于0(平方項/對角線元素有 ≤ 0 \le 0 ≤0的立即推不正定)
充要條件:所有順序主子式都大于0(一般是判斷某個項的系數取值)
如 [ 1 2 1 2 3 2 1 2 5 ] 的二階主子式 ∣ 1 2 2 3 ∣ 小于零 如\begin{bmatrix}1 &2 &1\\2&3&2\\1 &2&5\end{bmatrix}的二階主子式\begin{vmatrix}1 &2 \\2&3\end{vmatrix}小于零 如 ?121?232?125? ?的二階主子式 ?12?23? ?小于零
因為正定所以行列式大于0
正定必可逆
附錄1:相關結論的說明/例證
主對調,副變號
主對調副變號是求二階矩陣的
矩陣相似未必可以對角化
另一種說法是 A ~ B A \sim B A~B無法推出 A ~ Λ , B ~ Λ A \sim \Lambda,B\sim \Lambda A~Λ,B~Λ
如對于矩陣 A = ∣ 1 ? 2 0 1 ∣ B = ∣ 1 1 0 1 ∣ A=\begin{vmatrix} 1 & -2\\0&1 \end{vmatrix}\text{ } B=\begin{vmatrix} 1 & 1\\0&1 \end{vmatrix} A= ?10??21? ??B= ?10?11? ?
存在 p = ∣ 2 0 0 ? 1 ∣ p=\begin{vmatrix} 2 & 0\\0&-1 \end{vmatrix} p= ?20?0?1? ?使得 P ? 1 A P = B P^{-1}AP=B P?1AP=B,但是 A A A和 B B B均不可相似對角化。因為它們的特征值都為1(二重根),但是由于 2 ≠ n ? r ( E ? A ) 2 \neq n-r(E-A) 2=n?r(E?A)(其中 n = 2 n=2 n=2),故而無法相似對角化(但是確實相似)
A A A正定 ? A ? 1 \Leftrightarrow A^{-1} ?A?1正定
已知 A A A正定,又因為正定矩陣一定是實對稱矩陣,故有 A = A T A=A^T A=AT,對此式取逆,有 A ? 1 = ( A T ) ? 1 = ( A ? 1 ) T A^{-1}=(A^T)^{-1}=(A^{-1})^T A?1=(AT)?1=(A?1)T。
又因為 A A A的特征值 λ i \lambda_i λi?全大于0,所以 A ? 1 A^{-1} A?1的特征值 1 λ i \frac{1}{\lambda_i} λi?1?也全大于0
故有 A A A正定, A ? 1 A^{-1} A?1必正定
伴隨的情況也類似,但是為什么不能反推呢,有個反例:
A A A的三個特征值都是-1,此時 A ? A^* A?的三個特征值由 ? 1 × ? 1 × ? 1 ? 1 = 1 \frac{-1×-1×-1}{-1}=1 ?1?1×?1×?1?=1為正,這個反推不回去的
附錄2:一些可以橫向比較的概念辨析
矩陣的等價/相似/合同

如何形象地理解矩陣的相似與合同? - PeiLingX的回答 - 知乎
相似的矩陣是同一個線性變換在不同基下的矩陣。
合同的矩陣是同一個雙線性形在不同基下的矩陣。
相似必等價,等價未必相似。因為相似的 P ? 1 A P P^{-1}AP P?1AP中的 P ? 1 P^{-1} P?1就是等價中的 Q A P QAP QAP中的 Q Q Q
等價合同相似都得同型
- 等價:秩相等
- 相似:特征值相同或相似于同一對角陣(有重根得另外考慮,即特征值相同不一定相似)
- 合同:如果是實對稱矩陣得正負慣性指數相同
實對稱矩陣相似 ? 特征值相同 實對稱矩陣相似\Leftrightarrow特征值相同 實對稱矩陣相似?特征值相同

對稱和反對稱
若 A T = ? A A^T=-A AT=?A則為反對稱
- 主對角線為0,其余對應元素為相反數
對 A T = ? A A^T=-A AT=?A求行列式,則有 ∣ A ∣ = ∣ A T ∣ = ∣ ? A ∣ = ( ? 1 ) n ∣ A ∣ |A|=|A^T|=|-A|=(-1)^n|A| ∣A∣=∣AT∣=∣?A∣=(?1)n∣A∣
- 若反對稱矩陣行列式不為零則推知n為偶數
附錄3:收集的其他人有用的文章
我的意思是沒事時可以看看
矩陣跡(trace), 行列式(determinate)
線性代數小結02伴隨矩陣的十二個性質
22考研數學一143分經驗貼
附錄4:題型歸納與方法總結
x^n項系數
別忘乘逆序數
分塊矩陣
知乎 - 分塊矩陣行列式公式
秩1矩陣性質
AB=O
當兩個矩陣存在關系 A B = O AB=O AB=O并不意味著 A A A或 B B B為零矩陣。事實上 A B = O AB=O AB=O是 ∣ A ∣ ∣ B ∣ = 0 |A||B|=0 ∣A∣∣B∣=0的充分不必要條件。解該類問題的思考角度有:
- X = B ≠ 0 X=B≠0 X=B=0就是 A X = 0 AX=0 AX=0的非零解
- 從秩的角度入手
如 880.Z10.J.二.(8) 對 n n n階矩陣 A A A得到的 A ( A ? E ) = 0 且 A ≠ E A(A-E)=0且A\neq E A(A?E)=0且A=E
r ( A B ) ≤ min ? { r ( A ) , r ( B ) } r(AB)\le \min\{r(A),r(B)\} r(AB)≤min{r(A),r(B)}
矩陣的冪
- 若 A ~ B A\sim B A~B即 P ? 1 A P = B P^{-1}AP=B P?1AP=B則 A = P B P ? 1 A=PBP^{-1} A=PBP?1, A n = P B n P ? 1 A^n=PB^nP^{-1} An=PBnP?1
- 找規律(算 A 2 A^2 A2、 A 3 A^3 A3等)
- 若方陣 A A A有 r ( A ) = 1 r(A)=1 r(A)=1則有 A n = t r ( A ) n ? 1 A A^n=tr(A)^{n-1}A An=tr(A)n?1A,其中跡 t r ( A ) tr(A) tr(A)為對角線元素和,注意是原矩陣,不是化簡矩陣的跡
- 若 A = α β T A=\alpha \beta^T A=αβT則對于 A n = α β T α β T . . . α β T = α ( β T α ) ( β T α ) . . . ( β T α ) β T A^n = \alpha \beta^T\alpha \beta^T...\alpha\beta^T=\alpha (\beta^T\alpha )(\beta^T\alpha)...(\beta^T\alpha)\beta^T An=αβTαβT...αβT=α(βTα)(βTα)...(βTα)βT
- 分塊矩陣的冪運算規則(見下式)
[ A O O B ] n = [ A n O O B n ] \begin{bmatrix} A & O\\O&B \end{bmatrix}^n\text{ } =\begin{bmatrix} A^n & O\\O&B^n \end{bmatrix} [AO?OB?]n?=[AnO?OBn?]
6. 當分塊矩陣的塊退化到大小為1的時候,就變成了對角矩陣的乘冪的性質。
7. 組合數選擇,如 ( A + E ) n (A+E)^n (A+E)n,直接展開,在某些特殊冪次下 A m A^m Am可能等于0,這樣會把整個展開式消去絕大部分
上述的意思是 ( A + E ) n = ∑ i = 0 n C n i E n ? i A i (A+E)^n=\sum_{i=0}^nC_n^iE^{n-i}A^i (A+E)n=i=0∑n?Cni?En?iAi
線性相關
對于一個每個向量四維的向量組 α 1 α 2 α 3 \alpha_1\alpha_2\alpha_3 α1?α2?α3?判斷線性相關,由于其系數矩陣不是方陣,無法使用行列式來判斷,就得看系數矩陣的秩,有必要指出的是化簡時可以同乘含 t t t的倍數,下為例:
[ 1 2 0 0 1 1 0 0 3 ? t 0 0 2 + t ] \begin{bmatrix} 1 & 2 &0\\ 0 & 1 & 1\\ 0 &0&3-t \\ 0&0&2+t \end{bmatrix} ?1000?2100?013?t2+t? ?
此時若 t ≠ 3 t\neq 3 t=3且 t ≠ ? 2 t\neq -2 t=?2則 r ( A ) = 3 r(A)=3 r(A)=3,因為第三行除以 3 ? t 3-t 3?t,第四行除以 2 + t 2+t 2+t,兩行都變為1后可以消去一行
另一方面若 r ( A ) < 3 r(A)<3 r(A)<3則線性相關
若 A = ( α 1 α 2 . . . α n ) A=(\alpha_1\alpha_2...\alpha_n) A=(α1?α2?...αn?)是方陣則看行列式是否為0,為0則相關
線性表出
構造對稱矩陣
與轉置矩陣相加,即 a i i = b i i a i j = 1 2 ( b i j + b j i ) a_{ii}=b_{ii} \\ a_{ij}=\frac 12 (b_{ij}+b_{ji}) aii?=bii?aij?=21?(bij?+bji?)
A 2 = A A^2=A A2=A與特征值
設 A α = λ α , α ≠ 0 A\alpha = \lambda \alpha,\alpha \neq 0 Aα=λα,α=0則 A 2 α = λ 2 α A^2\alpha = \lambda ^2 \alpha A2α=λ2α,由 A 2 = 2 A A^2=2A A2=2A,則 ( λ 2 ? λ ) α = 0 (\lambda^2-\lambda)\alpha = 0 (λ2?λ)α=0。其中特征向量不能為0,則 λ 2 ? λ = 0 \lambda^2-\lambda=0 λ2?λ=0,顯然特征值分別是0或2
這時候通常是讓你確定二次型 A A A(對角矩陣)的,然后你就得把 0 0 0和 2 2 2往這個對角矩陣里填。題目中的其他條件會給出 A A A的秩,例如基礎解系的結構。
以 r ( A ) = 2 r(A)=2 r(A)=2為例,那就得填兩個 2 2 2進去,所以長下面這樣
[ 2 2 0 ] \begin{bmatrix}2\\&2\\&&0\end{bmatrix} ?2?2?0? ?
二次型中的 x T ( A T A ) x x^T(A^TA)x xT(ATA)x
這算是很多題型出現 x T ( A T A ) x x^T(A^TA)x xT(ATA)x后必有的中間運算固定套路
x T ( A T A ) x = ( x T A T ) ( A x ) = ( A x ) T ( A x ) x^T(A^TA)x=(x^TA^T)(Ax)=(Ax)^T(Ax) xT(ATA)x=(xTAT)(Ax)=(Ax)T(Ax)
A x Ax Ax是一個 n × n n×n n×n的矩陣和一個 n × 1 n×1 n×1的矩陣相乘,那結果就是 n × 1 n×1 n×1的列向量
設 A x = [ b 1 b 2 ? b n ] 故 ( A x ) T ( A x ) 的結果是 b 1 2 + b 2 2 + ? + b n 2 ≥ 0 設Ax=\begin{bmatrix}b_1\\b_2\\ \vdots \\b_n\end{bmatrix}故(Ax)^T(Ax)的結果是b_1^2+b_2^2+\cdots+b_n^2 \ge 0 設Ax= ?b1?b2??bn?? ?故(Ax)T(Ax)的結果是b12?+b22?+?+bn2?≥0
顯然有如下結論
- ( A x ) T ( A x ) > 0 ? ? b i ≠ 0 (Ax)^T(Ax)>0\Leftrightarrow \exist b_i \neq 0 (Ax)T(Ax)>0??bi?=0
- ( A x ) T ( A x ) = 0 ? ? b i = 0 (Ax)^T(Ax)=0\Leftrightarrow \forall b_i = 0 (Ax)T(Ax)=0??bi?=0
該結論常在證明正定時候使用,因為對于 ? x ≠ 0 \forall x \neq 0 ?x=0必有 ( A x ) T ( A x ) ≥ 0 (Ax)^T(Ax)\ge 0 (Ax)T(Ax)≥0
A + k E A+kE A+kE判斷相似
A = [ 2 0 0 0 2 2 0 0 2 ] B = [ 2 1 0 0 2 1 0 0 2 ] A=\begin{bmatrix}2&0&0\\0&2&2\\0&0&2\end{bmatrix} B=\begin{bmatrix}2&1 &0\\0&2&1\\0&0&2\end{bmatrix} A= ?200?020?022? ?B= ?200?120?012? ?
判斷上面的兩個矩陣是否相似
A ? 2 E = [ 0 0 0 0 0 2 0 0 0 ] , r ( A ? 2 E ) = 1 B ? 2 E = [ 0 1 0 0 0 1 0 0 0 ] , r ( B ? 2 E ) = 2 A-2E=\begin{bmatrix}0&0&0\\0&0&2\\0&0&0\end{bmatrix},r(A-2E)=1\\\text{}\\B-2E=\begin{bmatrix}0&1&0\\0&0&1\\0&0&0\end{bmatrix},r(B-2E)=2 A?2E= ?000?000?020? ?,r(A?2E)=1B?2E= ?000?100?010? ?,r(B?2E)=2
不相似
求過渡矩陣
欲求由 A A A到 B B B的過渡矩陣,即求可逆矩陣 P P P使得 B = A P B=AP B=AP,其做法是對 ( A ∣ B ) (A|B) (A∣B)做初等行變換,化為 ( E ∣ P ) (E|P) (E∣P),即為所求

)




)









)

的高維度單模態中介模型的參數估計(入門+實操))
