手寫 Attention 迷你LLaMa2—

https://github.com/Yuezhengrong/Implement-Attention-TinyLLaMa-from-scratch

1. Attention

1.1 Attention 靈魂10問

你怎么理解Attention？

Scaled Dot-Product Attention中的Scaled： $\frac{1}{\sqrt{d_k}}$ 的目的是調節內積，使其結果不至于太大（太大的話softmax后就非0即1了，不夠“soft”了）。

$\operatorname{Attention}(Q, K, V)=\operatorname{softmax}\left(\frac{Q K^T}{\sqrt{d_k}}\right) V$

Multi-Head可以理解為多個注意力模塊，期望不同注意力模塊“注意”到不一樣的地方，類似于CNN的Kernel。(注意：concat多頭輸出后需要再經過 $W^O$ )
$\begin{aligned} \operatorname{MultiHead}(Q, K, V) & =\operatorname{Concat}\left(\operatorname{head}_1, \ldots, \text { head }_{\mathrm{h}}\right) W^{Out} \\ \text { where head }_{\mathrm{i}} & =\operatorname{Attention}\left(Q W_i^Q, K W_i^K, V W_i^V\right) \end{aligned}$

乘性Attention和加性Attention有什么不同？

乘性Attention使用點積（dot product）來計算attention_score。具體而言，給定查詢（query）Q、鍵（key）K和值（value）V，乘性Attention通過計算內積來度量查詢和鍵之間的相似性，并使用softmax函數將得分歸一化為概率分布。計算公式如下：

$Attention(Q, K, V) = softmax(Q * K^T) * V$

乘性注意力的計算復雜度較低，因為它不需要引入額外的參數或矩陣運算。然而，由于點積的縮放問題，當查詢和鍵的維度較大時，乘性Attention可能會導致注意力權重過小或過大。

加性Attention使用額外的矩陣權重和非線性激活函數來計算attention_score。具體而言，給定查詢Q、鍵K和值V，加性Attention首先將Q和K通過一個矩陣W進行線性變換，然后應用激活函數（如tanh或ReLU），最后通過另一個矩陣U進行線性變換并使用softmax函數進行歸一化。計算公式如下：

$Attention(Q, K, V) = softmax(U * tanh(W_Q * Q + W_K * K)) * V$

加性Attention引入了額外的線性變換和非線性激活函數，因此計算復雜度較高。但它能夠更好地處理維度較大的查詢和鍵，并且具有更強的表示能力。

Self-Attention中的Scaled因子有什么作用？必須是 $\sqrt{d_k}$ 嗎？

在Self-Attention機制中，為了緩解點積計算可能導致的數值不穩定性和梯度消失或爆炸的問題，通常會引入一個縮放因子（scaling factor）。這個縮放因子通常是根號下key向量的維度（即 $\sqrt{d_k}$ ）。

但并不是絕對必須使用 $\sqrt{d_k}$ 。在實踐中，也可以根據具體情況調整縮放因子，例如使用1/d_k或其他系數來代替 $\sqrt{d_k}$ 。這取決于模型的架構設計、數據集特征以及訓練過程中的表現情況，可以根據實驗結果選擇合適的縮放因子。

Multi-Head Self-Attention，Multi越多越好嗎，為什么？

多頭注意力的優勢：

增加表示能力：每個注意頭可以關注輸入序列中不同位置的信息，學習到不同的特征表示。通過多個注意頭并行計算，模型能夠綜合利用多個子空間的信息，提高模型的表示能力。
提高泛化能力：多頭注意力有助于模型學習更豐富和復雜的特征表示，從而提高模型在各種任務上的泛化能力，減少過擬合的風險。

多頭注意力的限制：

計算復雜度增加：隨著注意頭數量的增加，計算復雜度會線性增加。更多的頭數意味著更多的參數和計算量，可能導致訓練和推理過程變得更加耗時。
過擬合風險：過多的注意頭可能導致模型過度擬合訓練數據，特別是在數據集較小或任務較簡單的情況下。過多的參數會增加模型的復雜度，增加過擬合的風險。

因此，并非多頭注意力中頭數越多越好，需要在表示能力和計算效率之間進行權衡。通常在實踐中，頭數的選擇是一種超參數，需要通過實驗和驗證集的性能來確定最佳的頭數。

Multi-Head Self-Attention，固定hidden_dim(即token_dim)時，你認為增加 head_dim （需要縮小 num_heads）和減少 head_dim 會對結果有什么影響？

在Multi-Head Self-Attention中，固定hidden_dim（隱藏層維度, 即token_dim）時，增加head_dim（每個注意頭的維度）和減少head_dim會對模型的表示能力和計算效率產生影響。這兩種調整會影響每個注意頭學習到的特征表示的維度，進而對模型整體的性能產生影響。

增加 head_dim（需要縮小 num_heads）：

增強每個注意頭的表達能力： 增加head_dim會增加每個注意頭學習到的特征表示的維度，使得每個注意頭能夠捕獲更豐富和復雜的特征信息，從而提高模型的表示能力。
減少注意頭的數量可能減少計算復雜度： 隨著head_dim的增加，為了保持總體隱藏層維度hidden_dim不變，可能需要減少注意頭的數量num_heads。減少注意頭的數量可以降低計算復雜度，因為每個注意頭的計算量隨著維度的增加而增加。
可能增加模型訓練的穩定性： 增加head_dim可以提高每個注意頭學習到的特征表示的豐富度，可能使得模型更容易學習到復雜的關系和模式，從而提高訓練的穩定性。

減少 head_dim：

降低每個注意頭的表達能力： 減少head_dim會降低每個注意頭學習到的特征表示的維度，可能限制每個注意頭捕獲和表示輸入序列的能力，導致模型的表示能力下降。
增加注意頭的數量可能提高模型的多樣性： 為了保持總體隱藏層維度hidden_dim不變，減少head_dim可能需要增加注意頭的數量num_heads。增加注意頭的數量可以增加模型學習不同方面信息的多樣性，有助于提高模型的泛化能力。
可能降低模型訓練的穩定性： 減少head_dim可能限制模型學習復雜關系的能力，使得模型更容易受到梯度消失或爆炸的影響，降低訓練的穩定性。

總體來說，增加head_dim可以提高每個注意頭的表達能力，而減少head_dim可能降低每個注意頭的表達能力。在選擇head_dim時，需要權衡模型的表示能力、計算效率以及訓練的穩定性，通常需要通過實驗來確定最佳的超參數設置。

為什么我們一般需要對 Attention weights 應用Dropout？哪些地方一般需要Dropout？Dropout在推理時是怎么執行的？你怎么理解Dropout？

在深度學習訓練中，對 Attention weights 應用 Dropout 的主要原因是為了減少過擬合。Attention機制通常用于提取輸入序列中的相關信息，但如果模型過度依賴某些輸入信息，就容易導致過擬合。通過引入 Dropout，可以隨機地將一部分 Attention weights 設置為零，從而減少模型依賴于特定輸入的情況，有助于提高模型的泛化能力。

一般來說，除了在 Attention weights 中使用 Dropout 外，還有一些情況下需要使用 Dropout，包括在全連接層、卷積層、循環神經網絡（RNN）等網絡結構中，都可以考慮使用 Dropout 來減少過擬合。

在推理時，Dropout 通常不會執行，因為在推理階段我們希望獲得穩定的預測結果，不需要隨機丟棄神經元。因此，在推理時，Dropout 層通常會被關閉，或者將每個神經元的輸出值按照訓練時的概率進行縮放。

Self-Attention的qkv初始化時，bias怎么設置，為什么？

在初始化 q、k、v 時，一般不會設置 bias (0)。

這是因為在 Self-Attention 中，Query、Key 和 Value 的計算通常是通過矩陣乘法來實現的，而不像全連接層那樣需要使用偏置項（bias）。對于 Self-Attention 的計算過程來說，沒有必要引入額外的偏置項，因為 Self-Attention 是通過計算 Query 和 Key 的點積得到 Attention weights，然后再將這些權重應用到 Value 上，不需要額外的偏置項來影響這個計算過程。

你認為Attention的缺點和不足是什么？

計算復雜度高： Attention 機制需要計算 Query 和 Key 之間的相似度，這通常需要進行矩陣乘法操作，導致計算復雜度較高，特別是在處理長序列時，計算量會進一步增加。
內存占用大：對于較長的序列，Attention 機制需要存儲大量的注意力權重，會占用大量內存，限制了模型能夠處理的序列長度。
缺乏位置信息：原始的 Self-Attention 沒有直接建模位置信息，雖然可以通過添加位置編碼來解決這個問題，但仍然存在局部關系建模不足的情況。
注意力偏向性：在處理長序列時，注意力容易偏向于關注距離較近的位置，難以捕捉長距離依賴關系，可能導致信息傳遞不及時或不完整。
對噪聲敏感： Attention 機制對輸入序列中的噪聲和異常值比較敏感，可能會影響模型的性能和魯棒性。
訓練過程中的穩定性：在訓練過程中，Attention 機制可能出現注意力集中或分散不均勻的情況，需要一定的技巧和調節來保持穩定的訓練效果。

你怎么理解Deep Learning的Deep？現在代碼里只有一個Attention，多疊加幾個效果會好嗎？

在深度學習中，“Deep” 指的是模型具有多層（深層）結構，通過堆疊多個隱藏層來提取數據的高級特征表示。深度神經網絡之所以稱為 “Deep Learning”，是因為相比于傳統淺層模型，它可以學習到更加抽象、復雜的特征表示，從而提高模型的表征能力。

在使用 Attention 機制時，通過堆疊多個 Attention 層，可以增加模型對輸入序列的建模能力和表示能力。這種多層 Attention 的堆疊通常被稱為 Multi-layer Attention，它可以讓模型在不同抽象層次上學習到更加復雜和深入的語義信息。

然而，需要注意的是，多層 Attention 的堆疊也會增加模型的復雜度和計算量，可能導致訓練過程變得更加困難和耗時。因此，在實際應用中，需要權衡模型性能和計算資源之間的關系，選擇合適的模型深度和結構來平衡精度和效率。

1.2 小項目：Self-Attention模型實現文本情感2分類

單層Attention Model：沒有實現W_out，反而加了Dropout。
$\begin{aligned} \operatorname{MultiHead}(Q, K, V) & =\operatorname{Concat}\left(\operatorname{head}_1, \ldots, \text { head }_{\mathrm{h}}\right) \\ \text { where head }_{\mathrm{i}} & =\operatorname{Attention}\left(Q W_i^Q, K W_i^K, V W_i^V\right) \end{aligned} \\ \operatorname{Attention}(Q, K, V)=Dropout(\operatorname{softmax}\left(\frac{Q K^T}{\sqrt{d_k}}\right)) V$

class SelfAttention(nn.Module):def __init__(self, config):super().__init__()self.config = configassert config.hidden_dim % config.num_heads == 0self.wq = nn.Linear(config.hidden_dim, config.hidden_dim, bias=False)self.wk = nn.Linear(config.hidden_dim, config.hidden_dim, bias=False)self.wv = nn.Linear(config.hidden_dim, config.hidden_dim, bias=False)self.att_dropout = nn.Dropout(config.dropout)def forward(self, x):batch_size, seq_len, hidden_dim = x.shapeq = self.wq(x)k = self.wk(x)v = self.wv(x)q = q.view(batch_size, seq_len, self.config.num_heads, self.config.head_dim)k = k.view(batch_size, seq_len, self.config.num_heads, self.config.head_dim)v = v.view(batch_size, seq_len, self.config.num_heads, self.config.head_dim)q = q.transpose(1, 2)k = k.transpose(1, 2)v = v.transpose(1, 2)# (b, nh, ql, hd) @ (b, nh, hd, kl) => b, nh, ql, klatt = torch.matmul(q, k.transpose(2, 3))att /= math.sqrt(self.config.head_dim)score = F.softmax(att.float(), dim=-1)score = self.att_dropout(score)# (b, nh, ql, kl) @ (b, nh, kl, hd) => b, nh, ql, hdattv = torch.matmul(score, v)attv = attv.view(batch_size, seq_len, -1)return score, attv

利用Attention Model實現NLP二分類模型：（num_labels=2）

Tokenizer：words[B,L] -> ids[B,L] （在模型外）
Embedding：ids[B,L] -> vectors[B,L,D]
SelfAttention：vectors[B,L,D] -> vectors[B,L,D]
Avg_Pooling：vectors[B,L,D] -> vectors[B,1,D]
Linear：vectors[B,D] -> vectors[B,num_labels]

class Model(nn.Module):def __init__(self, config):super().__init__()self.config = configself.emb = nn.Embedding(config.vocab_size, config.hidden_dim)self.attn = SelfAttention(config)self.fc = nn.Linear(config.hidden_dim, config.num_labels)def forward(self, x):batch_size, seq_len = x.shapeh = self.emb(x)attn_score, h = self.attn(h)h = F.avg_pool1d(h.permute(0, 2, 1), seq_len, 1)  # seq_len維度壓縮為1h = h.squeeze(-1)logits = self.fc(h)return attn_score, logits

后續代碼看github吧

2. LLaMa

2.1 LLaMa 靈魂10問

Tokenizer：words[B,L] -> ids[B,L]
Embedding：ids[B,L] -> vectors[B,L,D]
Transformer：vectors[B,L,D] -> vectors[B,L,D]
Sotfmax：vectors[B,L,D] -> logits[B,1,VS]

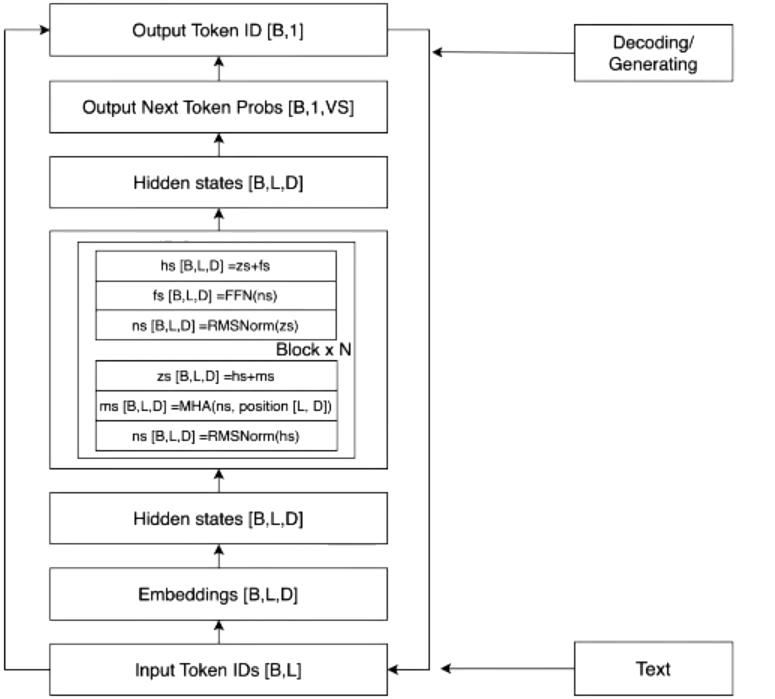
在這里插入圖片描述
這是一個相當深入和技術性的問題，我將依次回答你提出的每個問題。

Tokenize理解和方式區別
- Tokenize是將原始文本分割成標記（token）的過程，其中標記可以是單詞、子詞或字符。常見的Tokenize方式包括基于空格的分詞、基于規則的分詞、基于詞根的分詞（如WordPiece、Byte Pair Encoding）和字符級別的分詞。它們的區別在于分割粒度和表示能力，不同的Tokenize方式會影響模型對文本的理解和表示能力。
理想的Tokenizer模型特點
- 靈活性：能夠適應不同語言和文本類型的Tokenize需求。
- 高效性：快速處理大規模文本數據。
- 統一性：能夠生成統一的標記表示，以便模型統一處理。
特殊Token的作用和模型自動學習
- 特殊Token如開始和結束標記用于指示序列的起始和結束，使得模型能夠正確處理輸入序列。模型不能自動學習這些標記，因為在訓練中需要有明確的序列起始和結束的指示，而自動學習可能導致模糊性和不確定性。
LLM為何是Decoder-Only
- LLM是Decoder-Only是因為語言模型任務中，需要根據之前的文本預測下一個標記，這種順序建模的任務適合使用Decoder-Only結構。
RMSNorm和LayerNorm的區別

LayerNorm（層歸一化）：LayerNorm是一種常見的歸一化技術，它在每個層的特征維度上進行歸一化處理。具體來說，對于每個樣本，在特定層的所有隱藏單元特征維度上進行均值和方差的計算，然后將每個隱藏單元的輸出減去均值并除以標準差以實現歸一化。LayerNorm有助于加速訓練過程，并提高模型的泛化能力。
RMSNorm（根均方歸一化）：RMSNorm是另一種歸一化技術，它采用了不同的方式來計算歸一化的均值和方差。與LayerNorm不同，RMSNorm使用平方根均方（root mean square）來代替標準差。這意味著RMSNorm更側重于考慮樣本中的大值，從而更好地適應于序列數據，并能夠更好地處理長序列的梯度傳播問題。

總的來說，RMSNorm相比于LayerNorm更適用于序列數據，尤其是處理長序列時的效果更好。

LLM中的殘差連接和作用
- 殘差連接在LLM中用于保留輸入信息，有助于減少梯度消失和加速訓練。
PreNormalization和PostNormalization的影響

PreNormalization：在PreNormalization中，每個子層的輸入會先經過Layer Normalization（LN），然后是殘差連接（Residual Connection）和子層結構（比如Self-Attention或FFN）。這種順序能夠讓模型更好地傳遞信息和梯度，有利于減少梯度消失和加速訓練。因此，PreNormalization更利于信息傳遞和梯度傳播，有助于訓練深層模型。
PostNormalization：在PostNormalization中，每個子層的輸出會先經過子層結構，然后再經過LN和殘差連接。這種方式可能會導致梯度傳播時出現一些問題，因為LN的位置會影響到梯度的傳播路徑。相比之下，PostNormalization可能會導致一些梯度傳播上的困難，尤其是在深層網絡中。