導 讀

數據缺失可能會扭曲結果，降低統計功效，并且在某些情況下，導致估計有偏差，從而破壞從數據中得出的結論的可靠性。

處理缺失數據的傳統方法（例如剔除或均值插補）通常會引入自己的偏差或無法充分利用數據集中的可用信息。

鏈式方程插補 (MICE) 的出現為解決這一普遍問題提供了一種更復雜、更靈活的方法，為研究人員提供了一種可以處理現實世界數據固有的復雜性和不確定性的工具。

數據缺失的存在類似于在隱藏地形的地圖上導航。鏈式方程插補 (MICE) 方法充當指南針，引導研究人員穿過這些模糊的路徑，確保所采取的每一步都是最佳的，得出的每一個結論都盡可能準確。

有需要的朋友關注公眾號【小Z的科研日常】，獲取更多內容。

01、MCIE

鏈式方程插補 (MICE) 是一種用于處理數據集中缺失數據的統計技術。這是一種多功能方法，可以以靈活而穩健的方式處理缺失值，使其在社會科學到生物統計學等領域廣受歡迎。以下是詳細概述：

1.1 關鍵原則

① 多重插補：與使用單個估計值填充缺失值的單一插補方法不同，MICE 會生成多重插補。這種方法通過創建幾個不同的合理數據集來填充缺失值，從而承認缺失數據真實值的不確定性。

② 鏈式方程：MICE 通過使用一系列回歸模型在逐個變量的過程中估算缺失數據來進行操作。

每個缺失數據的變量都會有條件地估算到數據集中的其他變量。該過程是“鏈式的”，因為它迭代地循環變量，根據上一步的更新數據更新每一步的插補。

1.2 MICE如何運作？

① 初始化：缺失值最初用占位符值填充，通常是該變量觀測值的平均值或中位數。

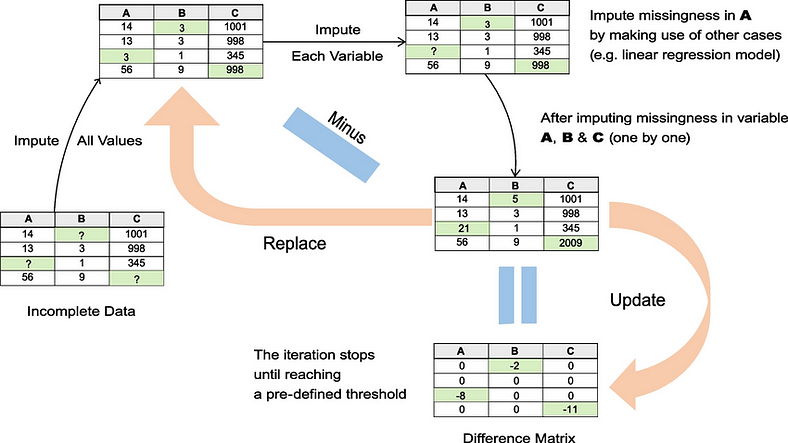
② 迭代：對于每個缺失數據的變量，使用其他變量作為預測變量，對觀測值擬合回歸模型。然后根據該模型估算缺失值。依次對每個變量重復此步驟，循環遍歷變量進行多次迭代。

③ 收斂：經過指定次數的迭代后，假定該過程已收斂，這意味著進一步循環變量不會顯著改變插補。

通常，前幾次迭代作為“老化”期被丟棄，并且通過從隨后的迭代中采樣來創建多個估算數據集。

1.3 MICE優點

• 靈活性：MICE 可以處理不同類型的變量（連續、二元、分類）和不同的缺失數據機制。

• 穩健性：通過生成多重插補，MICE 提供了一種量化由于缺失數據而導致的不確定性的方法，而這種不確定性在單一插補方法中經常被忽視。

• 效率：鏈式方程方法允許根據最適合其分布和與其他變量關系的模型來估算每個變量。

1.4 MICE局限性

• 假設：MICE 假設數據隨機丟失 (MAR)，但情況可能并非總是如此。如果數據不是隨機丟失 (MNAR)，則插補可能會有偏差。

• 復雜性：迭代過程以及生成和分析多個數據集的需要可能是計算密集型的，并且需要更復雜的統計分析。

1.5 應用領域

MICE廣泛應用于各個領域，在處理不完整數據集時進行數據分析。它在縱向研究、臨床試驗和調查中特別有用，因為丟失數據是一個常見問題。

通過提供穩健的缺失值輸入方法，MICE 幫助研究人員和分析師充分利用他們的數據，從而得出更準確、更可靠的結論。

1.6 MCIE的起源

MICE 源于更廣泛的多重插補框架，這是魯賓于 1987 年提出的一個概念，旨在通過創建多個插補數據集、單獨分析每個數據集，然后組合結果來解決因缺失數據而造成的不確定性。

MICE 在此基礎上構建，通過在鏈式迭代過程中采用一系列回歸模型來生成這些多重插補。這種方法創新使得能夠以更大的靈活性和準確性解決從健康科學到經濟學等不同領域的各種缺失數據問題。

1.7 MCIE的機制

MICE 的核心是通過迭代過程進行操作，其中每個缺失數據的變量都按順序進行估算，并使用其他變量作為預測變量。

該過程從初步插補階段開始，其中缺失值由初始估計值填充，例如觀測值的平均值或中位數。在連續迭代中，對于每個缺失數據的變量，將回歸模型擬合到觀察到的數據，同時考慮所有其他變量的當前插補。

然后根據該模型的預測分布估算缺失值。這個循環在一系列迭代中重復，使得插補隨著模型調整到反饋循環中的插補值而演變。

1.8 MCIE的優勢與創新

與傳統插補方法相比，MICE 方法具有多種優勢。

首先也是最重要的是它的靈活性：通過為每個變量選擇適當的模型，MICE 可以容納從連續到分類的不同類型和分布的變量。如果數據隨機丟失 (MAR) 的假設成立，這種適應性可以擴展到處理各種丟失模式和機制。

此外，通過生成多重插補，MICE 承認并量化插補過程中固有的不確定性，從而實現更穩健的統計推斷。

02、代碼

為了演示在 Python 中使用鏈式方程插補 (MICE)，我們將創建一個包含缺失值的合成數據集，應用 MICE 插補這些值，然后使用指標和圖評估插補質量。

我們將使用該pandas庫來處理數據、numpy生成缺失值、sklearn創建合成數據集和評估指標以及matplotlib繪圖seaborn。

我們還將使用IterativeImputerfrom，sklearn.impute因為它實現了類似 MICE 的方法。

import numpy as np
import pandas as pd
from sklearn.datasets import make_regression
from sklearn.experimental import enable_iterative_imputer
from sklearn.impute import IterativeImputer
from sklearn.metrics import mean_squared_error
import matplotlib.pyplot as plt
import seaborn as sns# 生成合成數據集
X, y = make_regression(n_samples=1000, n_features=10, noise=0.1, random_state=42)# 轉換為 DataFrame，以便于操作
df = pd.DataFrame(X, columns=[f'Feature_{i}' for i in range(X.shape[1])])
df['Target'] = y# 顯示前幾行
df.head()# I引入缺失值
np.random.seed(42)
df_missing = df.mask(np.random.random(df.shape) < 0.1)# 顯示前幾行以驗證缺失值
df_missing.head()# 初始化 MICE 計算器
mice_imputer = IterativeImputer(max_iter=10, random_state=42)# 擬合和轉換數據集以填補缺失值
df_imputed = mice_imputer.fit_transform(df_missing)# 將擬合數據轉換回 pandas DataFrame
df_imputed = pd.DataFrame(df_imputed, columns=df.columns)
df_imputed.head()# 計算每個特征的 RMSE
rmse = np.sqrt(mean_squared_error(df, df_imputed, multioutput='raw_values'))# 打印每個特征的均方根誤差
print(f'RMSE for each feature: {rmse}')# 選擇要繪制的特征
feature_to_plot = 'Feature_0'# 繪制原始分布圖和處理后的分布圖
plt.figure(figsize=(10, 6))
sns.kdeplot(df[feature_to_plot], label='Original', color='green', linestyle="--")
sns.kdeplot(df_imputed[feature_to_plot], label='Imputed', color='red', linestyle="-")
plt.legend()
plt.title(f'Distribution of Original vs. Imputed Values for {feature_to_plot}')
plt.xlabel('Value')
plt.ylabel('Density')
plt.show()

輸出：

RMSE for each feature: [ 0.24095716  0.22593846  0.21704334  0.15838514  0.25103187  0.299926050.1432319   0.22131897  0.27775888  0.16266519 15.56987127]

此代碼片段提供了從創建具有缺失值的合成數據集到使用 MICE 估算這些值并評估結果的完整演練。

它提供了一個在 Python 中處理缺失數據的實際示例，展示了 MICE 在保留數據集的統計屬性方面的實用性。

03、總結

鏈式方程插補代表了缺失數據處理方面的重大進步，為研究人員和分析師提供了靈活、強大且復雜的工具包。

雖然 MICE 具有一定的復雜性和假設，但它解決了統計分析中的基本挑戰，能夠對不完整的數據進行更明智、更細致的解釋。

隨著數據集規模和復雜性的增長，MICE 等先進插補技術的作用只會變得更加重要，這凸顯了統計科學中持續方法創新和教育的必要性。