01背包問題卡爾網 52. 攜帶研究材料

題目鏈接：52 攜帶研究材料

題干：小明是一位科學家，他需要參加一場重要的國際科學大會，以展示自己的最新研究成果。他需要帶一些研究材料，但是他的行李箱空間有限。這些研究材料包括實驗設備、文獻資料和實驗樣本等等，它們各自占據不同的重量，并且具有不同的價值。

小明的行李箱所能承擔的總重量為 N，問小明應該如何抉擇，才能攜帶最大價值的研究材料，每種研究材料可以選擇無數次，并且可以重復選擇。

• 輸入描述：

第一行包含兩個整數，N，V，分別表示研究材料的種類和行李空間?

接下來包含 N 行，每行兩個整數 wi 和 vi，代表第 i 種研究材料的重量和價值

• 輸出描述：

輸出一個整數，表示最大價值。

思考：此題為完全背包問題。01背包和完全背包唯一不同就是體現在遍歷順序上，所以直接針對遍歷順序分析。

01背包內嵌的循環是從大到小遍歷，為了保證每個物品僅被添加一次。而完全背包的物品是可以添加多次的，所以要從小到大去遍歷，保證物品可重復取，具體原因在01背包問題中講過。

但此處物品和背包容量遍歷順序可以調換。因為dp[j] 是根據 下標j之前所對應的dp[j]計算出來的。 只要保證下標j之前的dp[j]都是經過計算的就可以。

若先遍歷物品再遍歷背包則代碼如下：

// 先遍歷物品，再遍歷背包
for(int i = 0; i < weight.size(); i++) { // 遍歷物品for(int j = weight[i]; j <= bagWeight ; j++) { // 遍歷背包容量dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);}
}

若先遍歷背包再遍歷物品則代碼如下：

// 先遍歷背包，再遍歷物品
for(int j = 0; j <= bagWeight; j++) { // 遍歷背包容量for(int i = 0; i < weight.size(); i++) { // 遍歷物品if (j - weight[i] >= 0) dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);}cout << endl;
}

代碼：

#include<iostream>
#include<vector>
using namespace std;//采用滾動數組存儲的最大價值
int knapsack_1D(vector<int>& weight, vector<int>& value, int bagWeight) {//dp[j]表示背包空間為j的情況下，從所有物品里任取，能達到的最大價值vector<int> dp(bagWeight + 1, 0);for (int i = 0; i < weight.size(); i++)     //遍歷物品for (int j = weight[i]; j <= bagWeight; j++)     //遍歷背包重量dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);return dp[bagWeight];  
}int main() {int bagWeight, objectNum;cin >> objectNum >> bagWeight;vector<int> weight(objectNum, 0);vector<int> value(objectNum, 0);for (int i = 0; i < objectNum; i++) {cin >> weight[i];cin >> value[i];}cout << knapsack_1D(weight, value, bagWeight) << endl;system("pause");
}

Leetcode?518. 零錢兌換 II

題目鏈接：518 零錢兌換 II

題干：給你一個整數數組?coins?表示不同面額的硬幣，另給一個整數?amount?表示總金額。

請你計算并返回可以湊成總金額的硬幣組合數。如果任何硬幣組合都無法湊出總金額，返回?0?。

假設每一種面額的硬幣有無限個。?

題目數據保證結果符合 32 位帶符號整數。

思考：動態規劃。由于不同面額的硬幣可取多次，因此本題為完全背包的類似問題。

• 確定dp數組以及下標的含義

dp[j]：硬幣總額為i的組合個數

• 確定遞推公式

dp[j] 就是所有的dp[j - coins[i]]（考慮coins[i]的情況）相加。所以遞推公式：dp[j] += dp[j - coins[i]];

• dp數組如何初始化

從遞推公式可以看出，如果dp[0] = 0 的話，后面所有推導出來的值都是0。

下標非0的dp[j]初始化為0，這樣累計加dp[j - coins[i]]的時候才不會影響真正的dp[j]

• 確定遍歷順序

本題背包（硬幣總額）以及物品（硬幣）的先后遍歷順序與純完全背包不同，后者求得裝滿背包的最大價值是多少，和湊成總和的元素有沒有順序沒關系，即：有順序也行，沒有順序也行！

但本題要求湊成總和的組合數，元素之間明確要求沒有順序。因此要分別嘗試先遍歷物品（硬幣）以及先遍歷背包（硬幣總額）兩種情況。

---

嘗試先遍歷背包（硬幣總額）后遍歷物品（硬幣）會發現求出的是排列個數不是組合個數。舉例

硬幣面值只要1和2，要求硬幣總金額為3的組合個數。不難得到dp[1] = 1; dp[2] = 2;

在處理dp[3]時出現問題，按遞推公式dp [3] = dp [2]? + dp[1]，結果為3，而實際只有2種組合。

多出來的一種從哪來的呢？

從dp[2]：總金額為2組合分別為 {1，1}以及{2}，dp[1]：總金額為1組合為{1}

按遞推公式則將組合{1，2}和{2，1}都算一種組合，而這兩組合一樣。

而先遍歷物品（硬幣）后遍歷背包（硬幣總額）可行。

• 舉例推導dp數組

輸入: amount = 5, coins = [1, 2, 5] ，dp狀態圖如下：

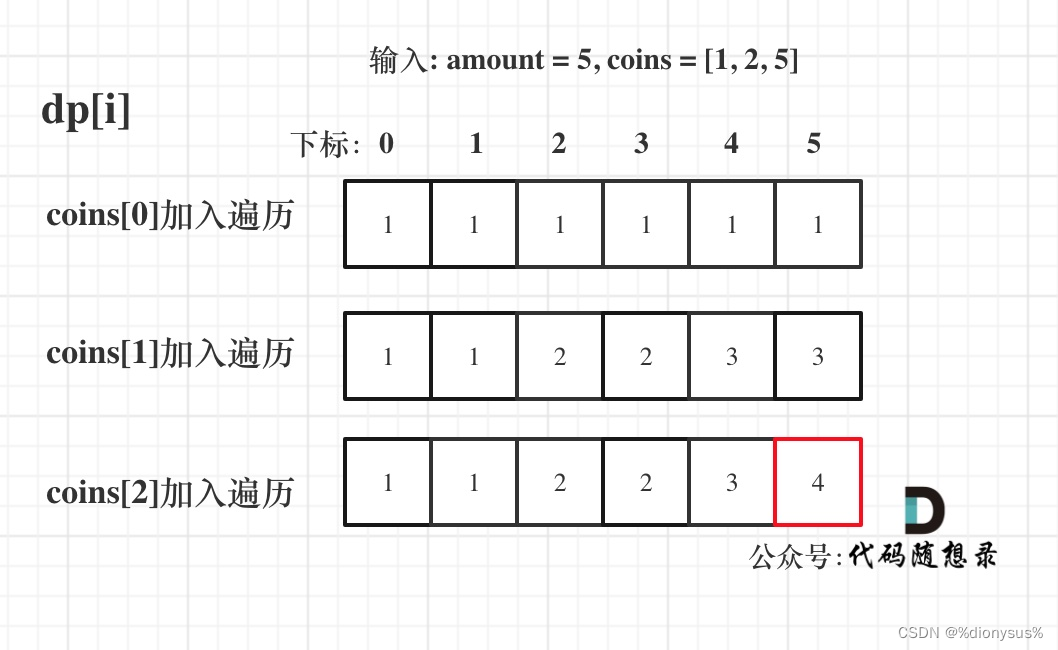
代碼：

class Solution {
public:int change(int amount, vector<int>& coins) {vector<int> dp(amount + 1, 0);      //dp[i]表示硬幣總額為i的組合個數dp[0] = 1;for (int i = 0; i < coins.size(); i++)          //遍歷硬幣for (int j = coins[i]; j <= amount; j++)    //遍歷硬幣總額dp[j] += dp[j - coins[i]];return dp[amount];}
};

Leetcode?377. 組合總和 Ⅳ

題目鏈接：377 組合總和 Ⅳ

題干：給你一個由?不同?整數組成的數組?nums?，和一個目標整數?target。請你從?nums?中找出并返回總和為?target?的元素組合的個數。

題目數據保證答案符合 32 位整數范圍。

請注意，順序不同的序列被視作不同的組合

思考：動態規劃。本題和上題幾乎一模一樣，唯一的區別在于本題順序不同的序列被視作不同的組合，因此只需要確定遍歷順序時將順序修改為先遍歷背包容量后遍歷物品即可。

由于本題有測試案例會超過int表示范圍的情況，因此在內層循環的判斷語句還要加上判斷條件dp[i] < INT_MAX - dp[i - nums[j]]。

代碼：

class Solution {
public:int combinationSum4(vector<int>& nums, int target) {vector<int> dp(target + 1, 0);      //dp[i]表示從數組中任取數字能達到累加和i的排列個數dp[0] = 1;for (int i = 0; i <= target; i++)           //遍歷累加和for (int j = 0; j < nums.size(); j++)   //遍歷數組if (i >= nums[j] && dp[i] < INT_MAX - dp[i - nums[j]])      //去處案例超過int表示范圍的情況dp[i] += dp[i - nums[j]];return dp[target];}

自我總結：

• ?確定遍歷順序的依據：遞推公式，數組內元素是否可重復取以及題干要求的是存在，組合還是排列。