我們來看一看一道比較難的問題（十分十分的巧妙）：

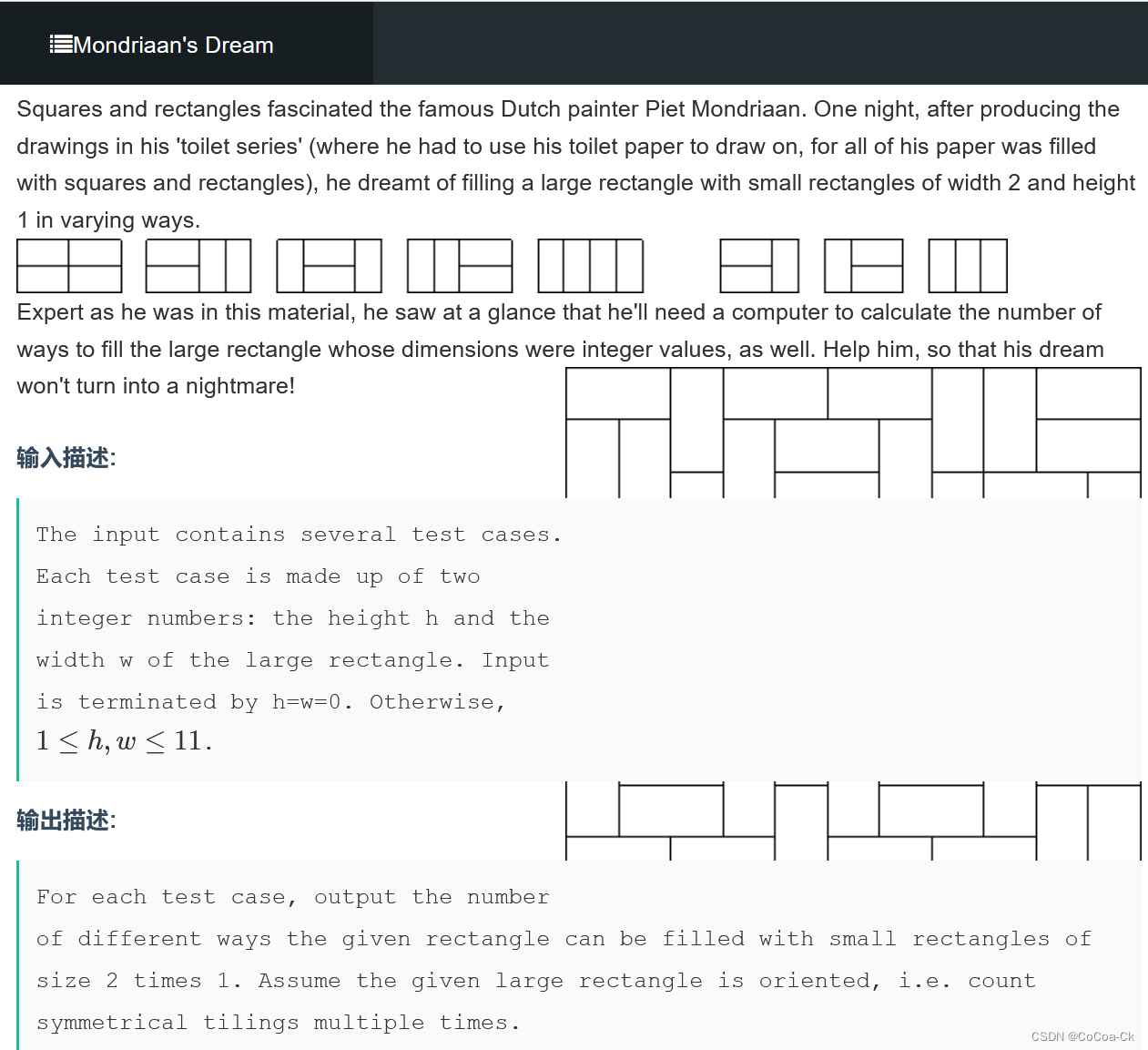
顯然我們應該一行一行放，又豎的會對下一行產生影響，我們令橫著放為0，豎著放的上方為1.

對于下一行，前一行放1的下面為0，但是會出現這么個情況：

10001,這3個0可能是豎著放的下方，也可以是一個橫放+1個豎著放的下方，而對于000下面的一定不能是3個0，只可以是100或001或111.

綜上，我們可以得到如下規則：

1.st&st'!=0是不可能的。

2.我們在忽略豎的0下不能有連續奇數的0.

顯然，對于一個01矩陣，它與1種方案是一一映射的。

有了這兩個規則，我們求的就是最后一行全為0的方案數。

但是，對于驗證第二個規則比較麻煩，我們如何用二進制的性質來化簡呢？

我們假設上一行為st1,本行為st2，我們取反st1,讓他-st2，這樣子我們就把豎的0忽略了。

我們只要計算是否有奇數的連續的1即可。

下面是AC代碼：

#include<bits/stdc++.h>
using namespace std;
int n,m;
long long dp[15][3000];
bool lian(int x){int cnt=0;int q=m;while(q--){if(x&1) cnt++;else{if(cnt%2==1) return 1;cnt=0;}x>>=1;}return cnt%2;
}
int main(){while(cin>>n>>m){if(n==0&&m==0) break;if(n*m%2) {printf("0\n");continue;}memset(dp,0,sizeof(dp));for(int i=0;i<=(1<<m)-1;i++){if(lian((~0)-i)==1) continue;dp[1][i]=1;}for(int i=2;i<=n;i++){for(int j=0;j<=(1<<m)-1;j++){for(int k=0;k<=(1<<m)-1;k++){if(k&j) continue;if(lian((~k)-j)==1) continue;dp[i][j]+=dp[i-1][k];}}}cout<<dp[n][0]<<endl;}
}