目錄

什么是回溯算法：

?子集問題：

子集問題II(元素可重復但不可復選):?

?組合問題：

組合問題II(元素可重復但不可復選):

排列問題：

排列問題II(元素可重復但不可復選):

---

什么是回溯算法：

「回溯是遞歸的副產品，只要有遞歸就會有回溯」，所以回溯法也經常和二叉樹遍歷，深度優先搜索混在一起，因為這兩種方式都使用了遞歸。

詳細地說：可以將回溯算法過程理解成一顆多叉樹的遍歷過程，?回溯法按深度優先策略搜索問題的解空間樹。首先從根節點出發搜索解空間樹，當算法搜索至解空間樹的某一節點時，先利用剪枝函數判斷該節點是否可行（即能得到問題的解）。如果不可行，則跳過對該節點為根的子樹的搜索，逐層向其祖先節點回溯；否則，進入該子樹，繼續按深度優先策略搜索。

回溯問題的基本框架：

void backtrack(參數) {if (終止條件) {存放結果;return;}for (選擇：本層集合中元素（樹中節點孩子的數量就是集合的大小）) {//注意i=0,i=start的區別處理節點;backtrack(路徑，選擇列表); // 遞歸  注意(i)和(i++)的區別  回溯，撤銷處理結果}
}

多叉樹的遍歷：

與二叉樹的遍歷類似，但要遍歷所有的子節點：

 public void traverse(TreeNode root){if(root == null){return ;}//前序遍歷的位置for(Node child : root.children){traverse(child);}//后序遍歷的位置}

?如果將前后續遍歷的位置放到for循環里面，與上圖的區別在于不遍歷根節點（通過后面例題加深理解）

那么有了上面的一定了解后，我們看下例題，具體怎么使用框架

?子集問題：

問題描述：

給你一個整數數組?nums?，數組中的元素?互不相同?。返回該數組所有可能的子集（冪集）。

解集?不能?包含重復的子集。你可以按?任意順序?返回解集。

?題目鏈接：78. 子集 - 力扣（LeetCode）

這是一個典型的回溯問題，首先，我們將它模擬成一顆多叉樹（根節點為空）：

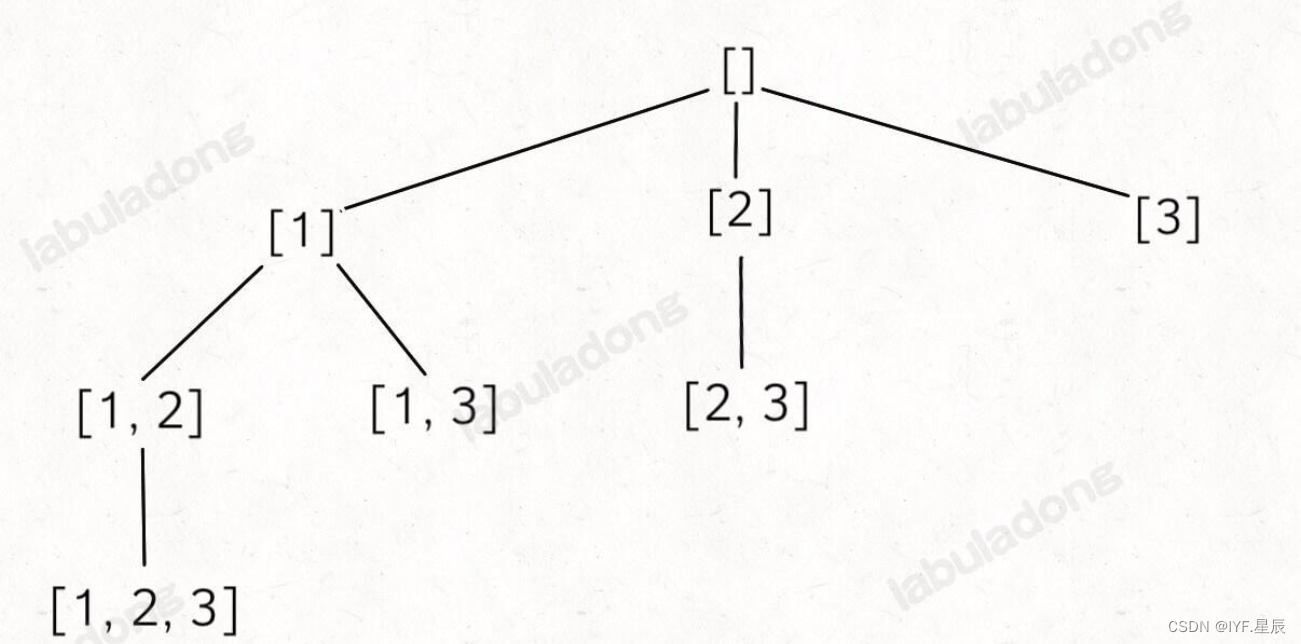
解決這個問題的關鍵在于如何遍歷這顆多叉樹，并且子集不重復?，在遍歷的過程中，我們要將每一個節點都收錄到集合中，最后返回這個集合。之后我們只需要讓子集不重復就好了，這里我們可以通過設定一個變量start來記錄當前走過的位置，使其不斷+1來進行迭代，保證不重復，具體實現如下：

class Solution {//定義二維數組res用于存儲結果List<List<Integer>> res = new LinkedList<>();//定義路徑數組LinkedList<Integer> track = new LinkedList<>(); public List<List<Integer>> subsets(int[] nums) {backtrack(nums,0);return res;}void backtrack(int[] nums,int start){//添加路徑數組到結果數組中res.add(new LinkedList<>(track));//for循環遍歷數組nums，這里相當于遍歷這顆多叉樹for(int i = start;i < nums.length;i++){//做選擇，將選擇添加到路徑數組中track.add(nums[i]);//回溯，繼續向后遍歷backtrack(nums,i + 1);//撤銷選擇，將選擇從路徑中刪除track.removeLast();}}
}

子集問題II(元素可重復但不可復選):?

題目鏈接：90. 子集 II - 力扣（LeetCode）

輸入輸出樣例：

這里我們以例一為例：為了區別兩個?2?是不同元素，后面我們寫作?nums = [1,2,2']。

按照之前的思路畫出子集的樹形結構，顯然，兩條值相同的相鄰樹枝會產生重復：

這里，我們需要進行剪枝，如果一個節點有多條值相同的樹枝相鄰，則只遍歷第一條，剩下的都剪掉，不要去遍歷：?

體現在代碼上，需要先進行排序，讓相同的元素靠在一起，如果發現?nums[i] == nums[i-1]，則跳過：

class Solution {List<List<Integer>> res = new LinkedList<>();LinkedList<Integer> track = new LinkedList<>();public List<List<Integer>> subsetsWithDup(int[] nums) {// 先排序，讓相同的元素靠在一起Arrays.sort(nums);backtrack(nums, 0);return res;}void backtrack(int[] nums, int start) {// 前序位置，每個節點的值都是一個子集，將他們收集res.add(new LinkedList<>(track));for (int i = start; i < nums.length; i++) {// 剪枝邏輯，值相同的相鄰樹枝，只遍歷第一條if (i > start && nums[i] == nums[i - 1]) {continue;}//選擇操作track.addLast(nums[i]);//回溯backtrack(nums, i + 1);//撤銷選擇track.removeLast();}}
}

?組合問題：

?題目描述：

給定兩個整數?n?和?k，返回范圍?[1, n]?中所有可能的?k?個數的組合。

你可以按?任何順序?返回答案。

輸入輸出：

示例 1：

輸入：n = 4, k = 2
輸出：
[[2,4],[3,4],[2,3],[1,2],[1,3],[1,4],
]

示例 2：

輸入：n = 1, k = 1
輸出：[[1]]

題目鏈接：77. 組合 - 力扣（LeetCode）

還是以?nums = [1,2,3]?為例，剛才讓我們求所有子集，就是把所有節點的值都收集起來；現在我們只需要把第 2 層（根節點視為第 0 層）的節點收集起來，就是大小為 2 的所有組合：

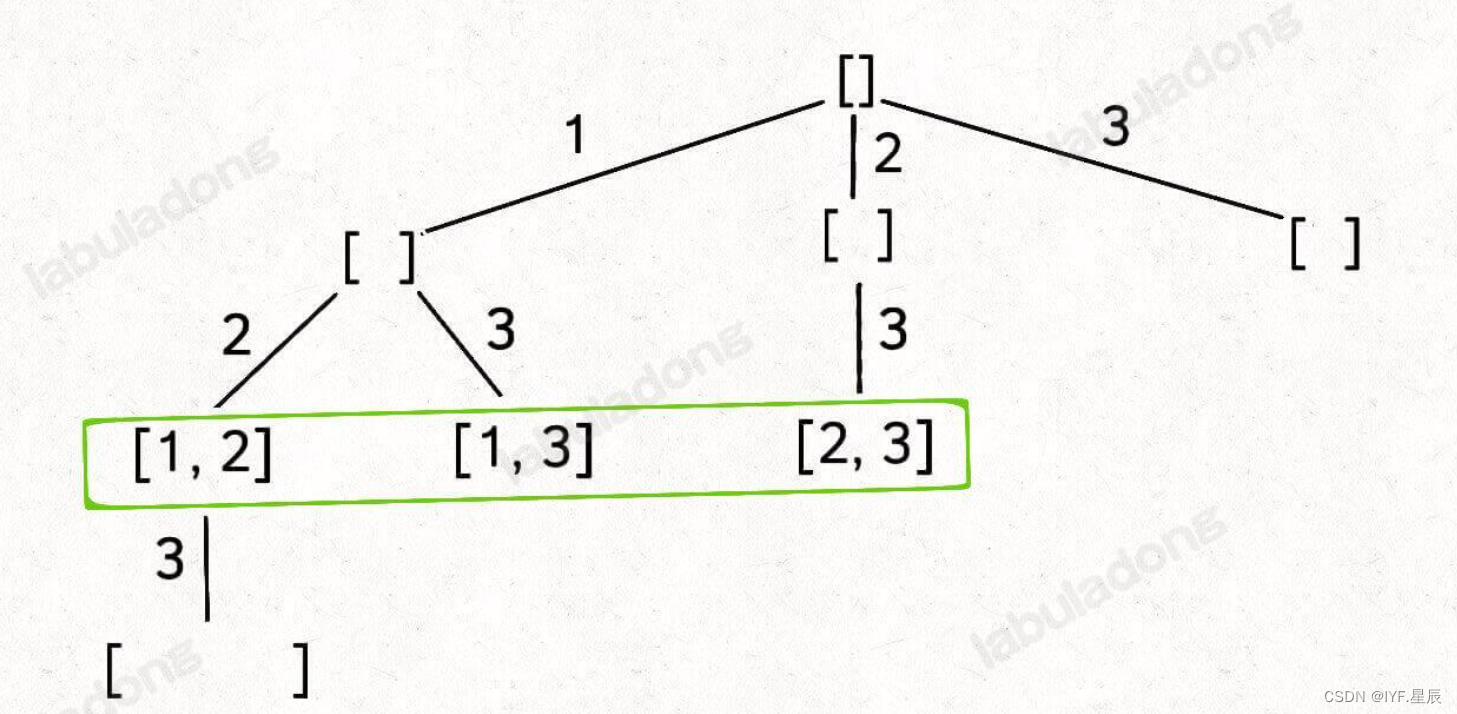
class Solution {List<List<Integer>> res = new LinkedList<>();// 記錄回溯算法的遞歸路徑LinkedList<Integer> track = new LinkedList<>();// 主函數public List<List<Integer>> combine(int n, int k) {backtrack(1, n, k);return res;}void backtrack(int start, int n, int k) {// base caseif (k == track.size()) {// 遍歷到了第 k 層，收集當前節點的值res.add(new LinkedList<>(track));return;}// 回溯算法標準框架for (int i = start; i <= n; i++) {// 選擇track.addLast(i);// 通過 start 參數控制樹枝的遍歷，避免產生重復的子集backtrack(i + 1, n, k);// 撤銷選擇track.removeLast();}}
}

組合問題II(元素可重復但不可復選):

題目描述：

給你一個?無重復元素?的整數數組?candidates?和一個目標整數?target?，找出?candidates?中可以使數字和為目標數?target?的 所有?不同組合?，并以列表形式返回。你可以按?任意順序?返回這些組合。

candidates?中的?同一個?數字可以?無限制重復被選取?。如果至少一個數字的被選數量不同，則兩種組合是不同的。?

對于給定的輸入，保證和為?target?的不同組合數少于?150?個。

題目鏈接：39. 組合總和 - 力扣（LeetCode）

上述子集問題中，我們通過變量start+1來控制樹的生成，也就是剪枝，但是這題可以無限制選用一個數字，那么剪枝也就沒有必要了，這里我們保持start不變（樹會一直生成），只需改變base case（限制條件）就行了，同時定義一個trackSum來維護路徑和：

class Solution {List<List<Integer>> res = new LinkedList<>();// 記錄回溯的路徑LinkedList<Integer> track = new LinkedList<>();// 記錄 track 中的路徑和int trackSum = 0;public List<List<Integer>> combinationSum(int[] candidates, int target) {if (candidates.length == 0) {return res;}backtrack(candidates, 0, target);return res;}// 回溯算法主函數void backtrack(int[] nums, int start, int target) {// base case，找到目標和，記錄結果if (trackSum == target) {res.add(new LinkedList<>(track));return;}// base case，超過目標和，停止向下遍歷if (trackSum > target) {return;}// 回溯算法標準框架for (int i = start; i < nums.length; i++) {// 選擇 nums[i]trackSum += nums[i];track.add(nums[i]);// 遞歸遍歷下一層回溯樹// 同一元素可重復使用，注意參數backtrack(nums, i, target);// 撤銷選擇 nums[i]trackSum -= nums[i];track.removeLast();}}
}

排列問題：

題目描述：給定一個不含重復數字的數組?nums?，返回其?所有可能的全排列?。你可以?按任意順序?返回答案。

題目鏈接：46. 全排列 - 力扣（LeetCode）?

剛才講的組合/子集問題使用?start?變量保證元素?nums[start]?之后只會出現?nums[start+1..]?中的元素，通過固定元素的相對位置保證不出現重復的子集。但排列問題本身就是讓你窮舉元素的位置，nums[i]?之后也可以出現?nums[i]?左邊的元素，所以之前的那一套玩不轉了，需要額外使用?used?數組來標記哪些元素還可以被選擇，這就相當于剪枝的作用。將全排列問題模擬成一顆多叉樹：

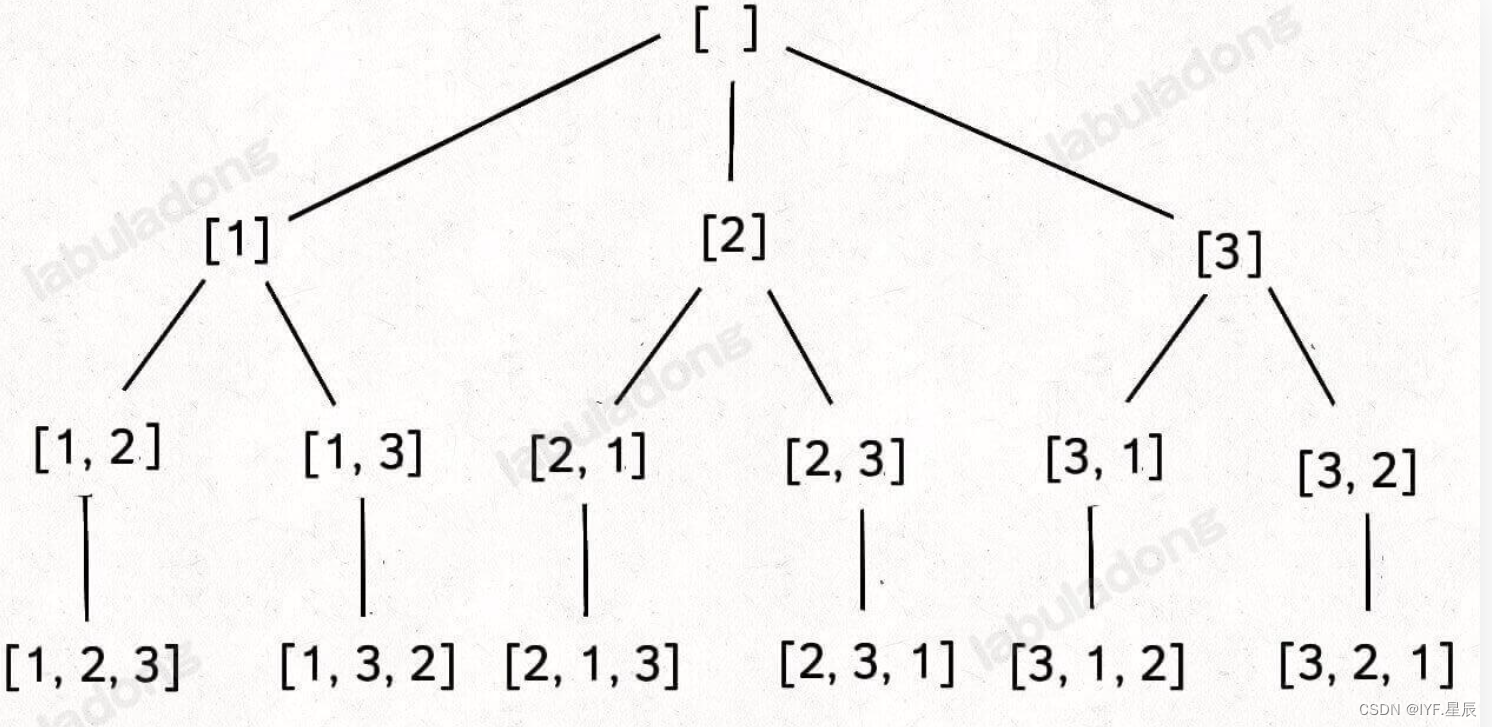
class Solution {List<List<Integer>> res = new LinkedList<>();// 記錄回溯算法的遞歸路徑LinkedList<Integer> track = new LinkedList<>();// track 中的元素會被標記為 trueboolean[] used;/* 主函數，輸入一組不重復的數字，返回它們的全排列 */public List<List<Integer>> permute(int[] nums) {used = new boolean[nums.length];backtrack(nums);return res;}// 回溯算法核心函數void backtrack(int[] nums) {// base case，到達葉子節點if (track.size() == nums.length) {// 收集葉子節點上的值res.add(new LinkedList(track));return;}// 回溯算法標準框架for (int i = 0; i < nums.length; i++) {// 已經存在 track 中的元素，不能重復選擇if (used[i]) {continue;}// 做選擇used[i] = true;track.addLast(nums[i]);// 進入下一層回溯樹backtrack(nums);// 取消選擇track.removeLast();used[i] = false;}}
}

排列問題II(元素可重復但不可復選):

比如輸入?nums = [1,2,3]，那么這種條件下的全排列共有 3^3 = 27 種：

[[1,1,1],[1,1,2],[1,1,3],[1,2,1],[1,2,2],[1,2,3],[1,3,1],[1,3,2],[1,3,3],[2,1,1],[2,1,2],[2,1,3],[2,2,1],[2,2,2],[2,2,3],[2,3,1],[2,3,2],[2,3,3],[3,1,1],[3,1,2],[3,1,3],[3,2,1],[3,2,2],[3,2,3],[3,3,1],[3,3,2],[3,3,3]
]

標準的全排列算法利用?used?數組進行剪枝，避免重復使用同一個元素。如果允許重復使用元素的話，直接放飛自我，去除所有?used?數組的剪枝邏輯就行了。

代碼詳解：

class Solution {List<List<Integer>> res = new LinkedList<>();LinkedList<Integer> track = new LinkedList<>();public List<List<Integer>> permuteRepeat(int[] nums) {backtrack(nums);return res;}// 回溯算法核心函數void backtrack(int[] nums) {// base case，到達葉子節點if (track.size() == nums.length) {// 收集葉子節點上的值res.add(new LinkedList(track));return;}// 回溯算法標準框架for (int i = 0; i < nums.length; i++) {// 做選擇track.add(nums[i]);// 進入下一層回溯樹backtrack(nums);// 取消選擇track.removeLast();}}
}

最后總結：

回溯算法本質就是個多叉樹的遍歷問題，關鍵就是在前序遍歷和后序遍歷的位置做一些操作，算法框架如下：

void backtrack(參數) {if (終止條件) {存放結果;return;}for (選擇：本層集合中元素（樹中節點孩子的數量就是集合的大小）) {//注意i=0,i=start的區別處理節點;backtrack(路徑，選擇列表); // 遞歸  注意(i)和(i++)的區別  回溯，撤銷處理結果}
}

寫?backtrack?函數時，需要維護走過的「路徑」和當前可以做的「選擇列表」，當觸發「結束條件」時，將「路徑」記入結果集。?最后返回結果集合，得到答案。

結語：?寫博客不僅僅是為了分享學習經歷，同時這也有利于我鞏固自己的知識點，總結該知識點，由于作者水平有限，對文章有任何問題的還請指出，接受大家的批評，讓我改進。同時也希望讀者們不吝嗇你們的點贊+關注+收藏，你們的鼓勵是我創作的最大動力！