知識出處：Hello算法：https://www.hello-algo.com/

文章目錄

• • 2.4 樹
  • • 2.4.1 「二叉樹 binary tree」
    • • 2.4.1.1 二叉樹基本操作
      • 2.4.1.2 二叉樹的常見類型
      • • 「完美二叉樹 perfect binary tree」
        • 「完全二叉樹 complete binary tree」
        • 「完滿二叉樹 full binary tree」
        • 「平衡二叉樹 balanced binary tree」
      • 2.4.1.3 二叉樹的退化&進化
    • 2.4.2 二叉樹遍歷
    • • 2.4.2.1 層序遍歷 level-order traversal
      • • 代碼
        • 復雜度分析
      • 2.4.2.2 前序、中序和后序遍歷（DFS）
      • • 深度優先搜索通常基于遞歸實現。
        • 深度優先遍歷基于迭代的方式實現
    • 2.4.3 二叉樹數組表示
    • • 2.4.3.1 數組表示完美二叉樹
      • 2.4.3.2 數組表示任意二叉樹
      • 2.4.3.3 優點與局限性
    • 2.4.4 二叉搜索樹
    • • 2.4.4.1 二叉搜索樹的搜索操作
      • • 查詢
        • 插入節點
        • 中序遍歷
      • 2.4.4.2 搜索二叉樹的效率
      • 2.4.4.3 二叉搜索樹常見應用

2.4 樹

2.4.1 「二叉樹 binary tree」

二叉樹 binary tree是一種非線性數據結構，代表“祖先”與“后代”之間的派生關系，體現了“一分為二”的分治邏輯。與鏈表類似，二叉樹的基本單元是節點，每個節點包含值、左子節點引用和右子節點引用。

/* 二叉樹節點類 */
class TreeNode {int val;         // 節點值TreeNode left;   // 左子節點引用TreeNode right;  // 右子節點引用TreeNode(int x) { val = x; }
}

• 每個節點都有兩個引用（指針），分別指向「左子節點 left-child node」和「右子節點 right-child node」

• 該節點自身被稱為這兩個子節點的「父節點 parent node」.

• 當給定一個二叉樹的節點時，我們將該節點的左子節點及其以下節點形成的樹稱為該節點的「左子樹 left subtree」，同理可得「右子樹 right subtree」。

• 在二叉樹中，除葉節點外，其他所有節點都包含子節點和非空子樹。也就是說，不包含子節點的節點就被稱為「葉節點 leaf node」

二叉樹的常用術語如圖所示。

• 「根節點 root node」：位于二叉樹頂層的節點，沒有父節點。
• 「葉節點 leaf node」：沒有子節點的節點，其兩個指針均指向 None 。
• 「邊 edge」：連接兩個節點的線段，即節點引用（指針）。
• 節點所在的「層 level」：從頂至底遞增，根節點所在層為 1 。
• 節點的「度 degree」：節點的子節點的數量。在二叉樹中，度的取值范圍是 0、1、2 。
• 二叉樹的「高度 height」：從根節點到最遠葉節點所經過的邊的數量。
• 節點的「深度 depth」：從根節點到該節點所經過的邊的數量。
• 節點的「高度 height」：從距離該節點最遠的葉節點到該節點所經過的邊的數量。

Tip:

• 請注意，我們通常將“高度”和“深度”定義為“經過的邊的數量”，但有些題目或教材可能會將其定義為“經過的節點的數量”。在這種情況下，高度和深度都需要加 1 。
• 如何理解深度和高度？
  • 深度是根部到該節點的舉例，高度是該節點到葉節點的距離
  • 深度可以表示找到這個節點需要花費的時間，深度越深，找到這個節點就經過更多邊，也需要更多時間。可以用于判斷“查詢”操作所需的時間
  • 高度可以表示從這個節點到最外層需要花費的時間，高度越高，找到葉節點的時間就需要花費更多時間。可以用于判斷遍歷“該子樹所有節點”所需的時間。
  • 另外，深度只能描述某個節點的深度，而高度既可以直接表示樹，也可以描述某個節點。

2.4.1.1 二叉樹基本操作

初始化

與鏈表類似，首先初始化節點，然后構建引用（指針）。

插入與刪除節點

與鏈表類似，在二叉樹中插入與刪除節點可以通過修改指針來實現

注意：

插入節點可能會改變二叉樹的原有邏輯結構，而刪除節點通常意味著刪除該節點及其所有子樹。因此，在二叉樹中，插入與刪除通常是由一套操作配合完成的，以實現有實際意義的操作。

2.4.1.2 二叉樹的常見類型

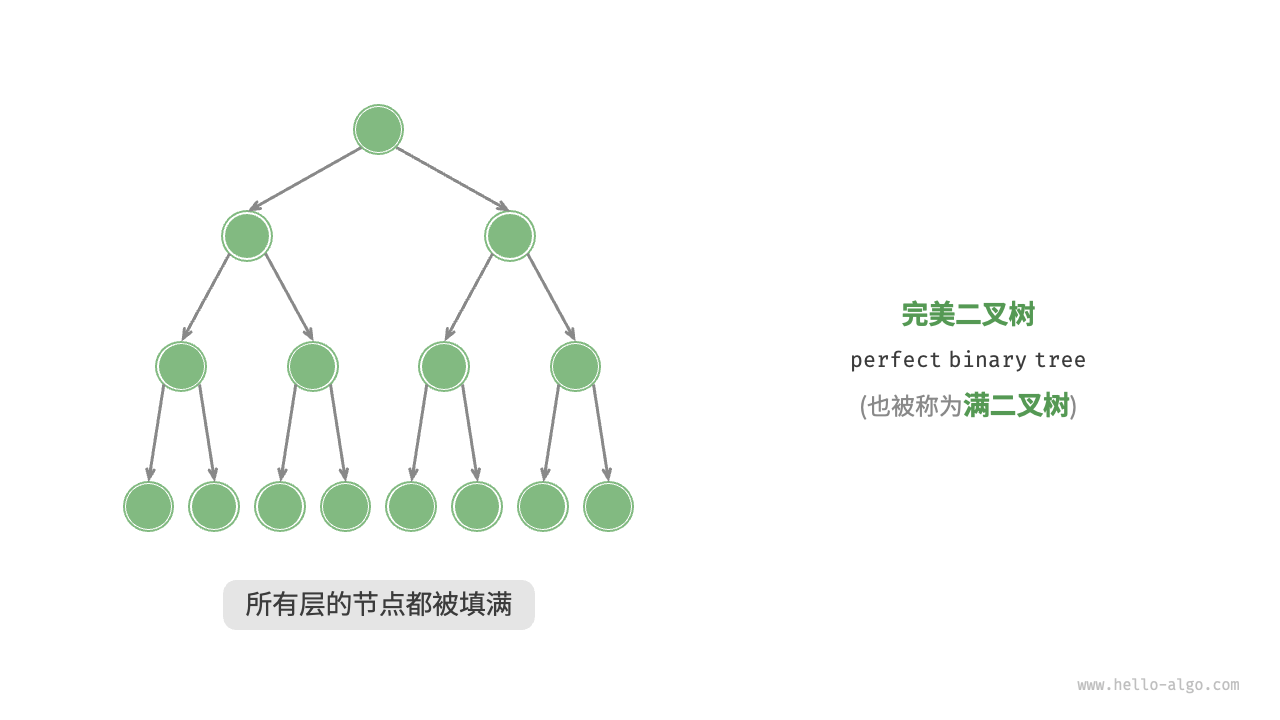
「完美二叉樹 perfect binary tree」

完美二叉樹（又稱“滿二叉樹”）是所有層的節點都被完全填滿的二叉樹，具有以下特點：

• 所有葉節點的度都為0，且其余所有節點都為0；
• 若樹的高度為h，則節點總數為 2^h+1?1 。呈指數級關系，反應了自然界中的細胞分裂現象。

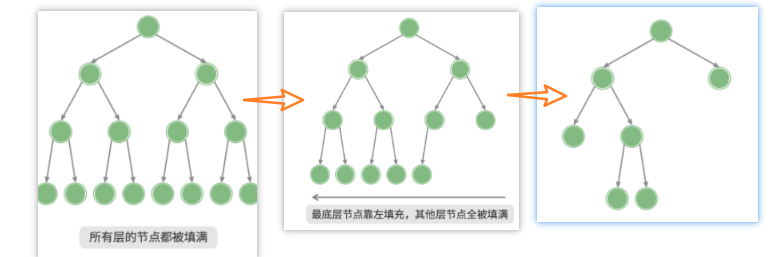
「完全二叉樹 complete binary tree」

只有最底層的節點未被填滿，且最底層節點盡量靠左填充。

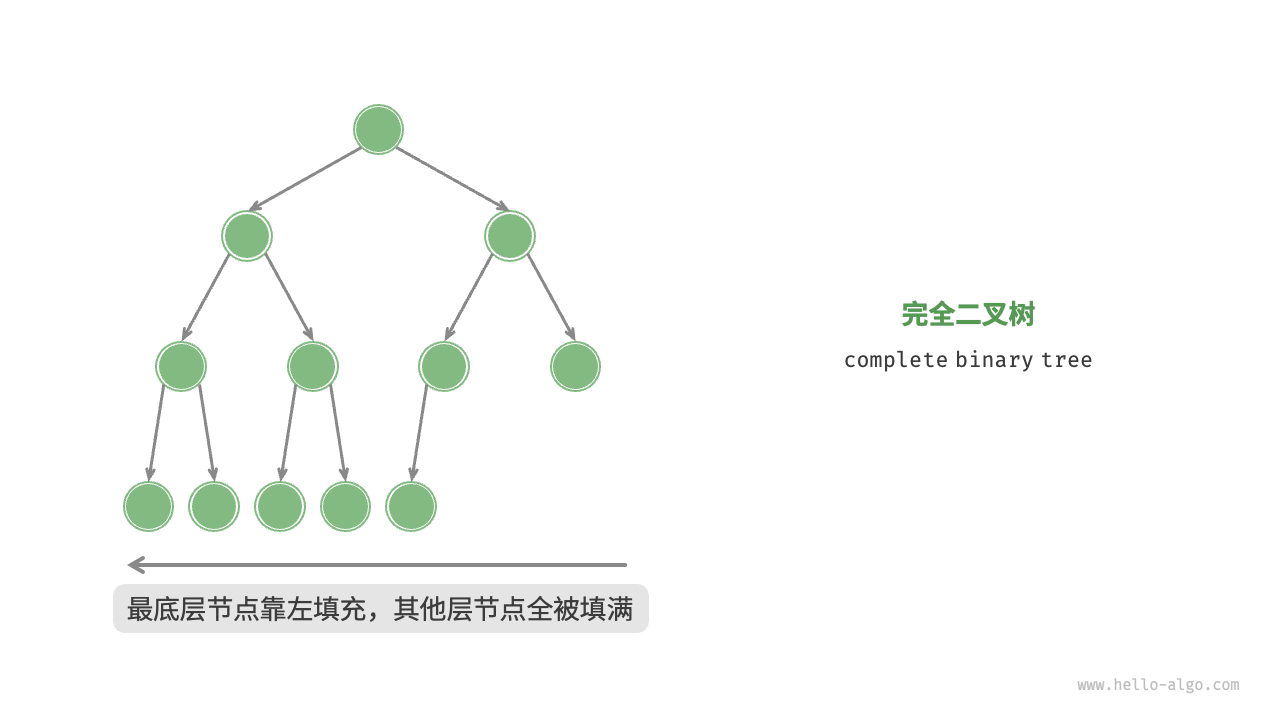
之前被忽略的類型，實際上這樣的二叉樹可以直接使用數組進行表示，需要有將一維序列轉換換位二維序列的思維能力。

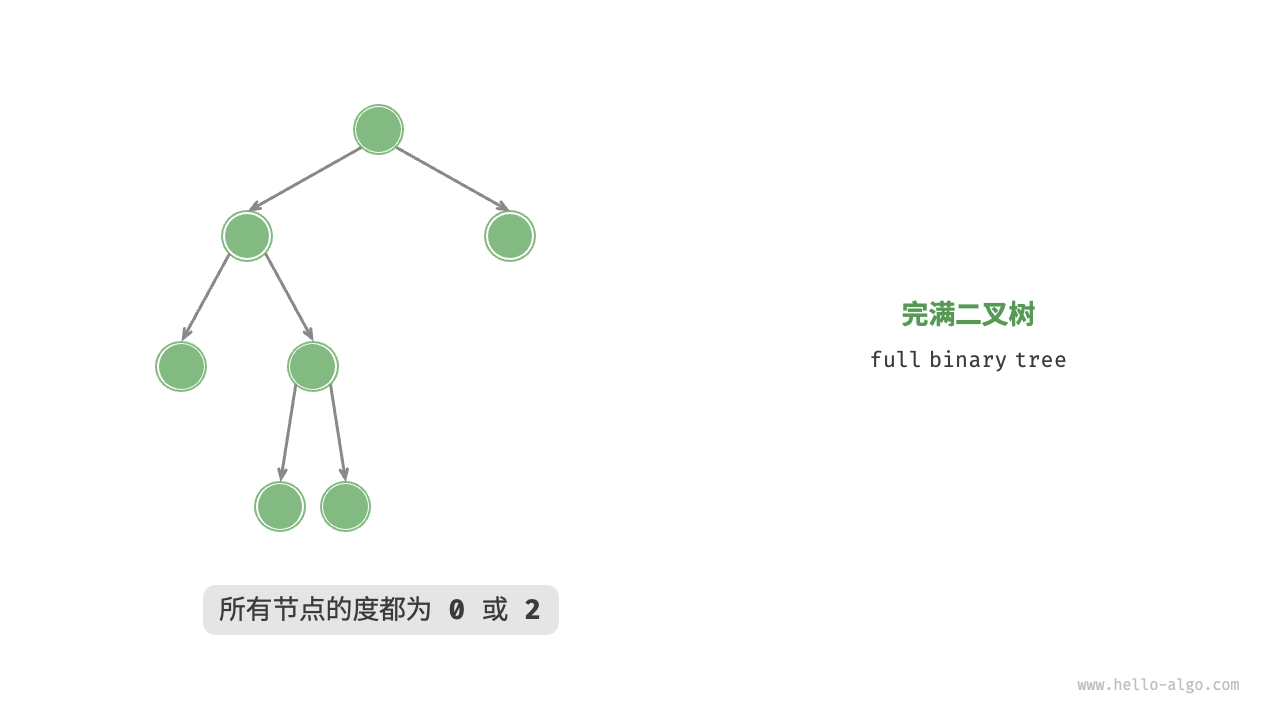
「完滿二叉樹 full binary tree」

除了葉節點之外，其余所有節點都有兩個子節點。

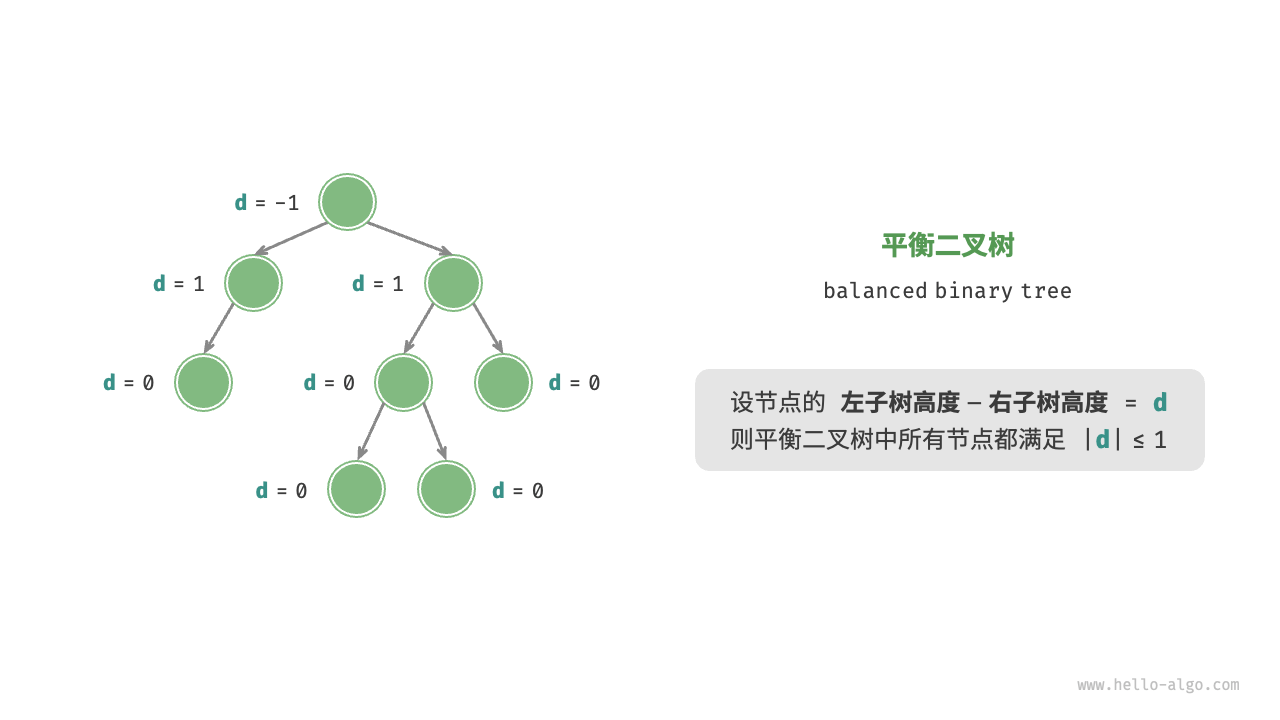
「平衡二叉樹 balanced binary tree」

任意節點的左子樹和右子樹的高度之差的絕對值不超過 1 。

2.4.1.3 二叉樹的退化&進化

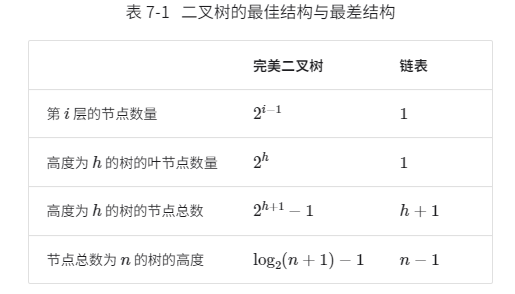
當二叉樹的每層節點都被填滿時，達到“完美二叉樹”；而當所有節點都偏向一側時，二叉樹退化為“鏈表”。

在最佳結構和最差結構下，二叉樹的葉節點數量、節點總數、高度等達到極大值或極小值。

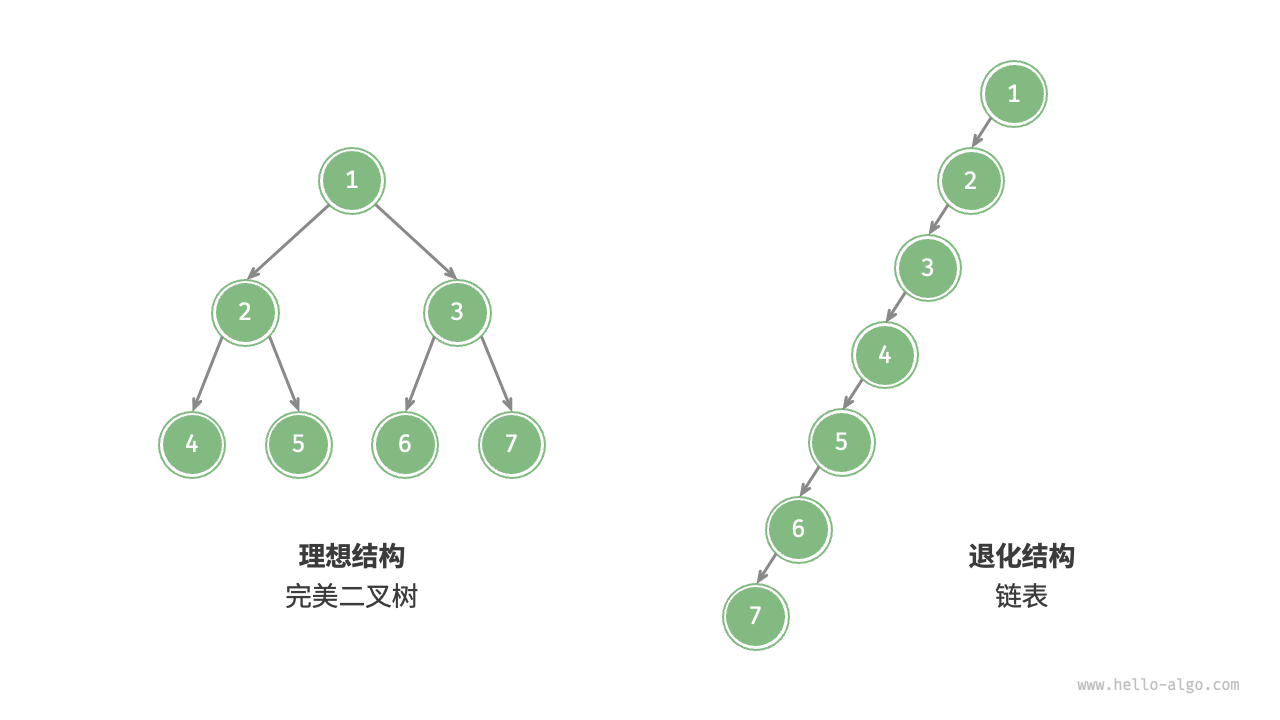
關于二叉樹演變的個人理解

• 鏈表可以看成“所有節點的度都為1的二叉樹”，是一種特化的二叉樹，理論上適用于二叉樹的計算公式，也適用于鏈表。反過來，鏈表擁有的部分特點在會在二叉樹上實現。
• 二叉樹的幾種常用類型也有自身的演化過程：
  1. 平衡二叉樹（左子樹和右子樹相差不大即可
  2. 圓滿二叉樹（非葉節點都有兩個子節點）
  3. 完全二叉樹（在圓滿二叉樹的基礎上，要求節點都靠左）
  4. 完美二叉樹（在完全二叉樹的基礎上，要求葉節點這層的節點都必須被填滿）

2.4.2 二叉樹遍歷

鏈表的遍歷方式是通過指針逐個訪問節點。然而，從物理結構的角度來看，樹是一種基于鏈表的非線性數據結構，這使得遍歷樹比遍歷鏈表更加復雜，需要借助搜索算法來實現。

二叉樹常見的遍歷方式包括層序遍歷、前序遍歷、中序遍歷和后序遍歷等。(手敲代碼幫助理解)

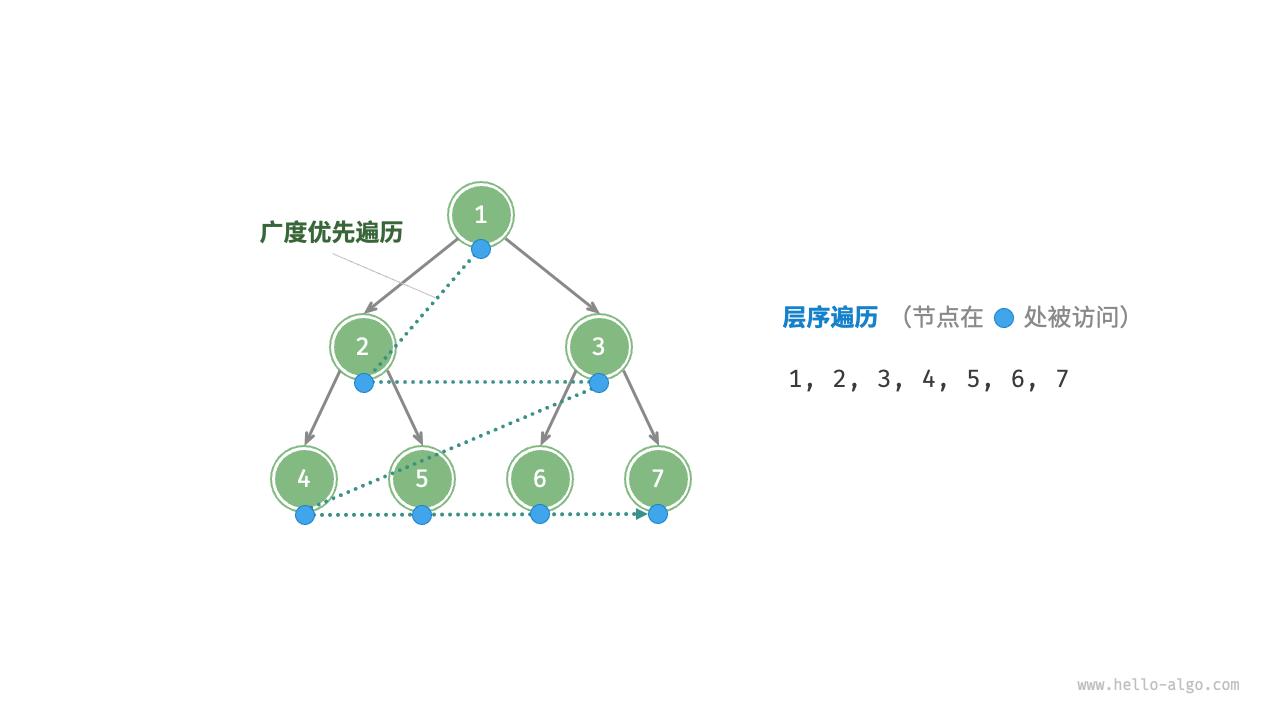
2.4.2.1 層序遍歷 level-order traversal

從頂部到底部逐層遍歷二叉樹，并在每一層按照從左到右的順序訪問節點。

層序遍歷本質上屬于**「廣度優先遍歷 breadth-first traversal」，也稱「廣度優先搜索 breadth-first search, BFS」**，它體現了一種“一圈一圈向外擴展”的逐層遍歷方式。

代碼

廣度優先遍歷通常借助“隊列”來實現。

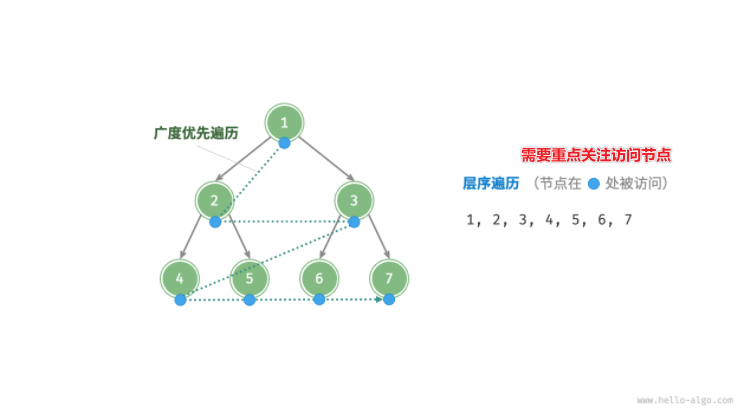
實現思路如下：

1. 給出一個隊列，先存入根節點； 給出一個列表，用于存儲結果
2. 遍歷該隊列
   • 節點出隊
   • 像列表，存入數值
   • 將出隊的節點對應的節點（如有）入隊
   • 以此循環

// 層序遍歷
Queue<TreeNode> treeNodeQueue = new ArrayDeque<>();
treeNodeQueue.add(n1);
List<Integer> resList = new ArrayList<>();
while (!treeNodeQueue.isEmpty()){TreeNode node = treeNodeQueue.poll();resList.add(node.val);if (node.left != null){treeNodeQueue.add(node.left);}if (node.right != null){treeNodeQueue.add(node.right);}
}

復雜度分析

• 時間復雜度為 O(n) ：所有節點被訪問一次，使用 O(n) 時間，其中 n 為節點數量。
• 空間復雜度為 O(n) ：在最差情況下，即滿二叉樹時，遍歷到最底層之前，隊列中最多同時存在 (n+1)/2 個節點，占用 O(n) 空間。

2.4.2.2 前序、中序和后序遍歷（DFS）

相應地，前序、中序和后序遍歷都屬于**「深度優先遍歷 depth-first traversal**」，也稱「深度優先搜索 depth-first search, DFS」，它體現了一種“先走到盡頭，再回溯繼續”的遍歷方式。

深度優先遍歷就像是繞著整棵二叉樹的外圍“走”一圈，在每個節點都會遇到三個位置，分別對應前序遍歷、中序遍歷和后序遍歷，

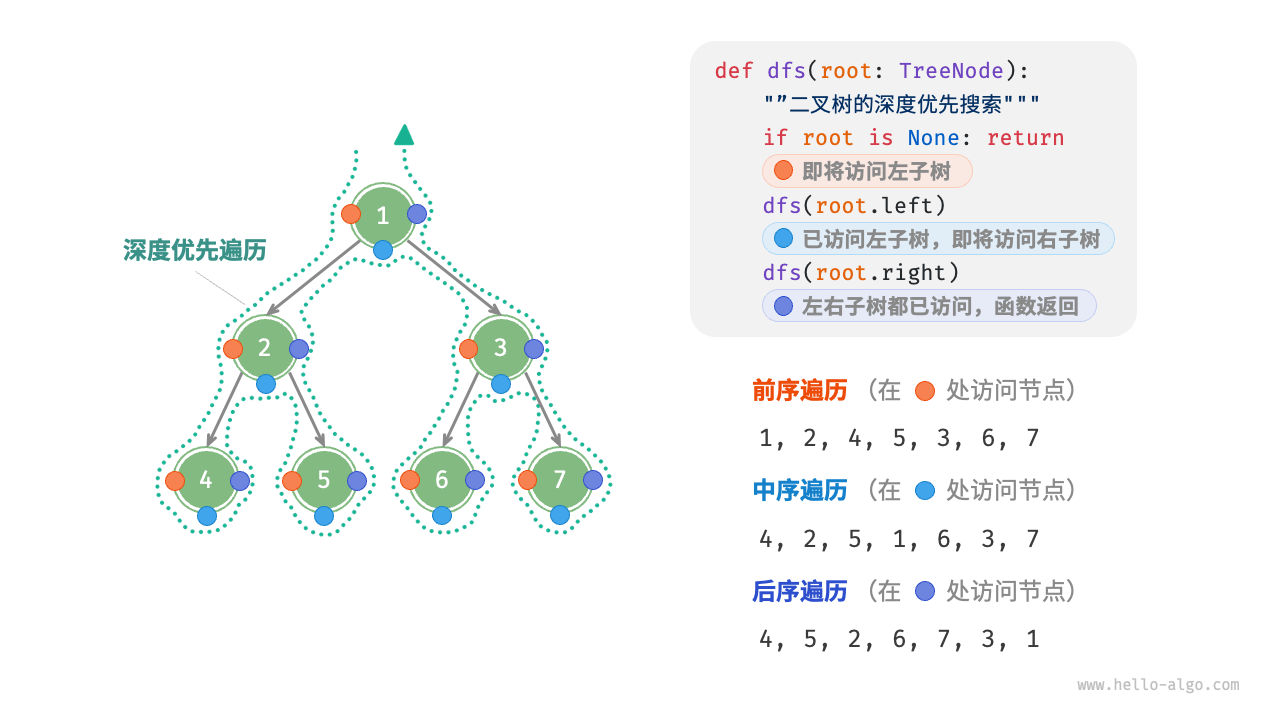
深度優先搜索通常基于遞歸實現。

遞歸過程，可分為“遞”和“歸”兩個逆向的部分。

1. “遞”表示開啟新方法，程序在此過程中訪問下一個節點。
2. “歸”表示函數返回，代表當前節點已經訪問完畢。

public static void main(String[] args) {/* 初始化二叉樹 */// 初始化節點TreeNode n1 = new TreeNode(1);TreeNode n2 = new TreeNode(2);TreeNode n3 = new TreeNode(3);TreeNode n4 = new TreeNode(4);TreeNode n5 = new TreeNode(5);TreeNode n6 = new TreeNode(6);TreeNode n7 = new TreeNode(7);// 構建節點之間的引用（指針）n1.left = n2;n1.right = n3;n2.left = n4;n2.right = n5;n3.left = n6;n3.right = n7;System.out.println("\n初始化二叉樹\n");PrintUtil.printTree(n1);resList.clear();preOrder(n1, resList);System.out.println(resList);resList.clear();midOrder(n1, resList);System.out.println(resList);resList.clear();afterOrder(n1, resList);System.out.println(resList);
}/*** 前序遍歷*/
static void preOrder(TreeNode node, List<Integer> res) {if (node == null) {return;}// 遍歷節點本身res.add(node.val);// 遍歷左節點preOrder(node.left, res);// 遍歷右節點preOrder(node.right, res);
}static void midOrder(TreeNode node, List<Integer> res) {if (node == null) {return;}// 遍歷左節點preOrder(node.left, res);// 遍歷節點本身res.add(node.val);// 遍歷右節點preOrder(node.right, res);
}static void afterOrder(TreeNode node, List<Integer> res) {if (node == null) {return;}// 遍歷左節點preOrder(node.right, res);// 遍歷右節點preOrder(node.left, res);// 遍歷節點本身res.add(node.val);
}

深度優先遍歷基于迭代的方式實現

力扣找到的解法：解答思路

我們也可以用迭代的方式實現方法一的遞歸函數，兩種方式是等價的，區別在于遞歸的時候隱式地維護了一個棧，而我們在迭代的時候需要顯式地將這個棧模擬出來，其余的實現與細節都相同，具體可以參考下面的代碼。

Stack<TreeNode> stack = new Stack<>();
TreeNode node = n1;
List<Integer> res = new ArrayList<Integer>();
while (!stack.isEmpty() || node != null) {while (node != null) {res.add(node.val);stack.push(node);node = node.left;}node = stack.pop();node = node.right;
}

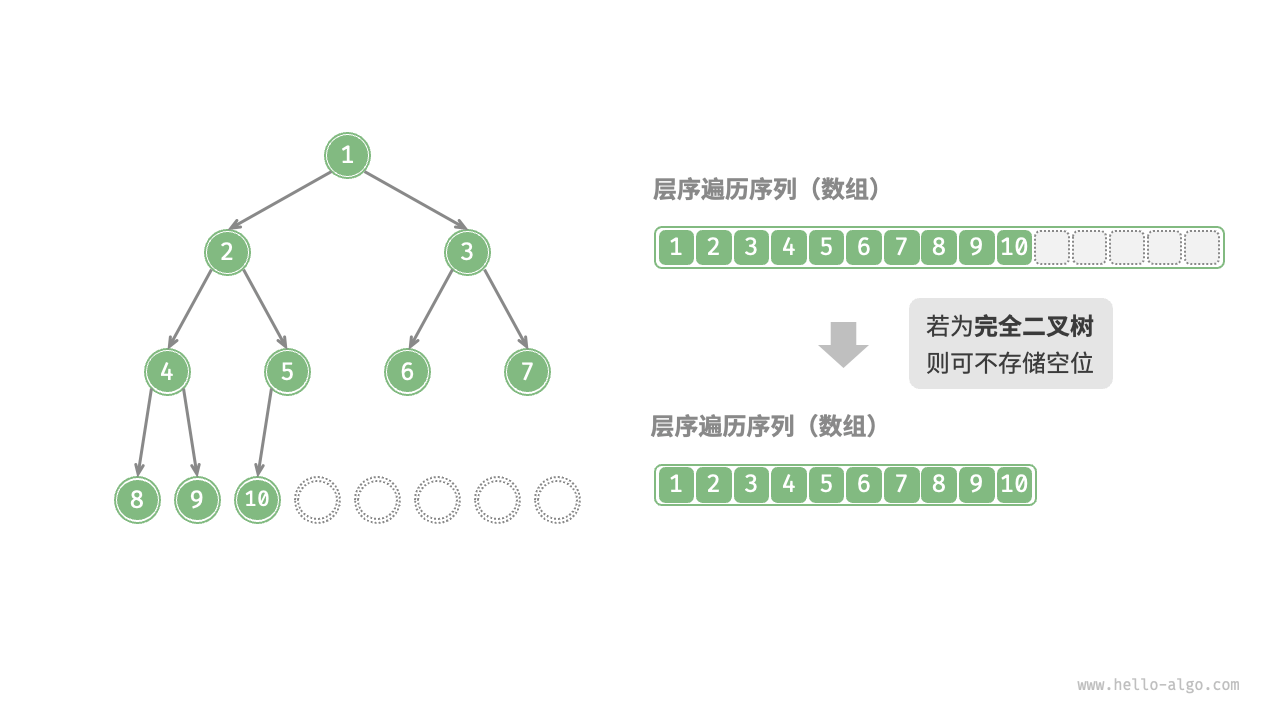
2.4.3 二叉樹數組表示

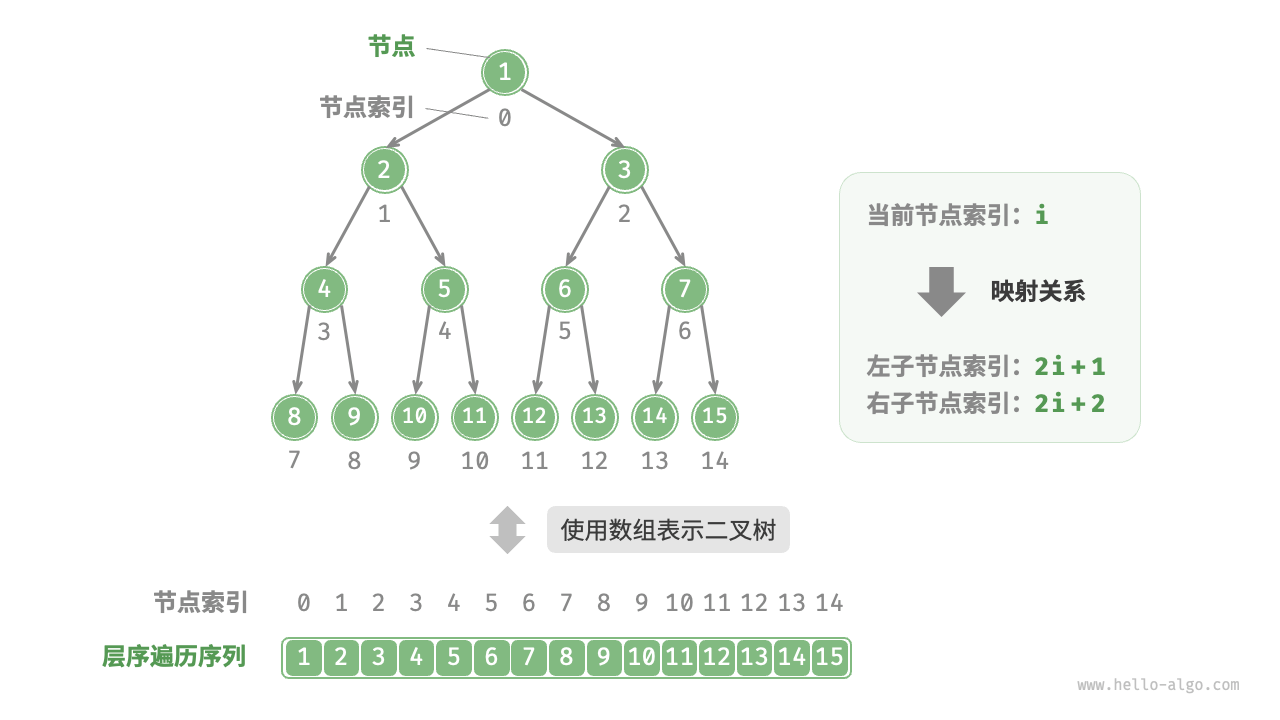
2.4.3.1 數組表示完美二叉樹

原文中給出的圖非常直觀的展示了數組如何表示二叉樹

2.4.3.2 數組表示任意二叉樹

在上面的基礎上，顯式地寫出所有 None

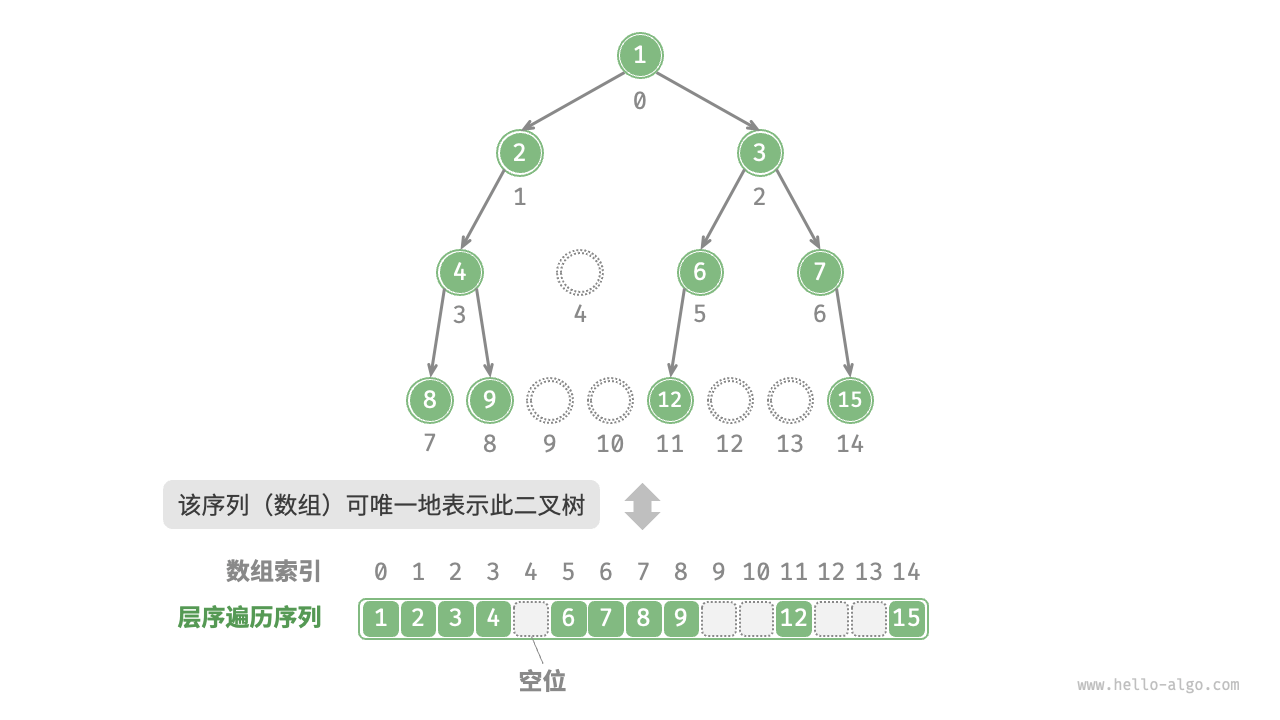
綜上不難發現，，完全二叉樹非常適合使用數組來表示。回顧完全二叉樹的定義，None 只出現在最底層且靠右的位置，因此所有 None 一定出現在層序遍歷序列的末尾。

代碼實現

嘗試用List<Integer>來表示的二叉樹，實現以下操作：

• 給定某節點，獲取它的值、左（右）子節點、父節點。
• 獲取前序遍歷、中序遍歷、后序遍歷、層序遍歷序列。

2.4.3.3 優點與局限性

二叉樹的數組表示主要有以下優點。

• 數組存儲在連續的內存空間中，對緩存友好，訪問與遍歷速度較快。
• 不需要存儲指針，比較節省空間。
• 允許隨機訪問節點。

然而，數組表示也存在一些局限性。

• 數組存儲需要連續內存空間，因此不適合存儲數據量過大的樹。
• 增刪節點需要通過數組插入與刪除操作實現，效率較低。
• 當二叉樹中存在大量 None 時，數組中包含的節點數據比重較低，空間利用率較低。

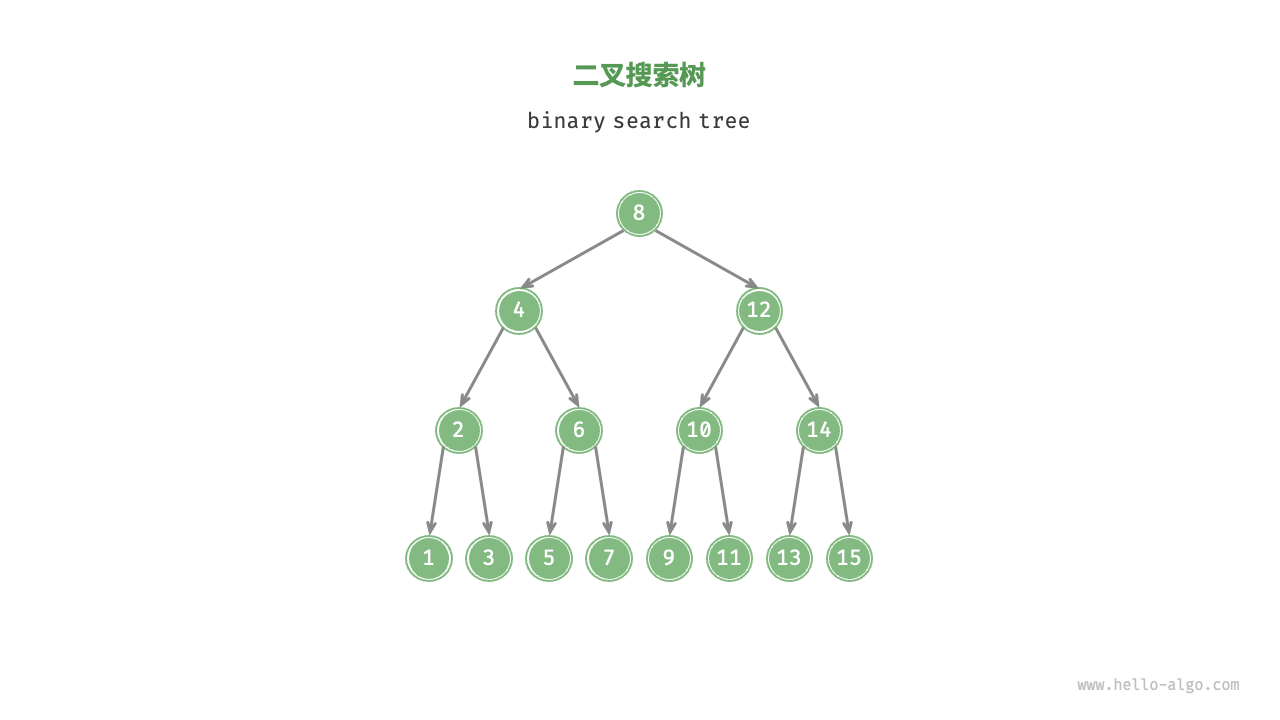
2.4.4 二叉搜索樹

「二叉搜索樹 binary search tree」滿足以下條件。

1. 對于根節點，左子樹中所有節點的值 < 根節點的值 < 右子樹中所有節點的值。
2. 任意節點的左、右子樹也是二叉搜索樹，即同樣滿足條件 1. 。

和“堆”的概念近似，也要做出區分。

• 「小頂堆 min heap」：任意節點的值 ≤ 其子節點的值。
• 「大頂堆 max heap」：任意節點的值 ≥ 其子節點的值。

個人理解：

• 二叉搜索樹體現了二分算法的思想

2.4.4.1 二叉搜索樹的搜索操作

查詢

給定目標節點值 num ，可以根據二叉搜索樹的性質來查找。如圖 7-17 所示，我們聲明一個節點 cur ，從二叉樹的根節點 root 出發，循環比較節點值 cur.val 和 num 之間的大小關系。

• 若 cur.val < num ，說明目標節點在 cur 的右子樹中，因此執行 cur = cur.right 。
• 若 cur.val > num ，說明目標節點在 cur 的左子樹中，因此執行 cur = cur.left 。
• 若 cur.val = num ，說明找到目標節點，跳出循環并返回該節點。

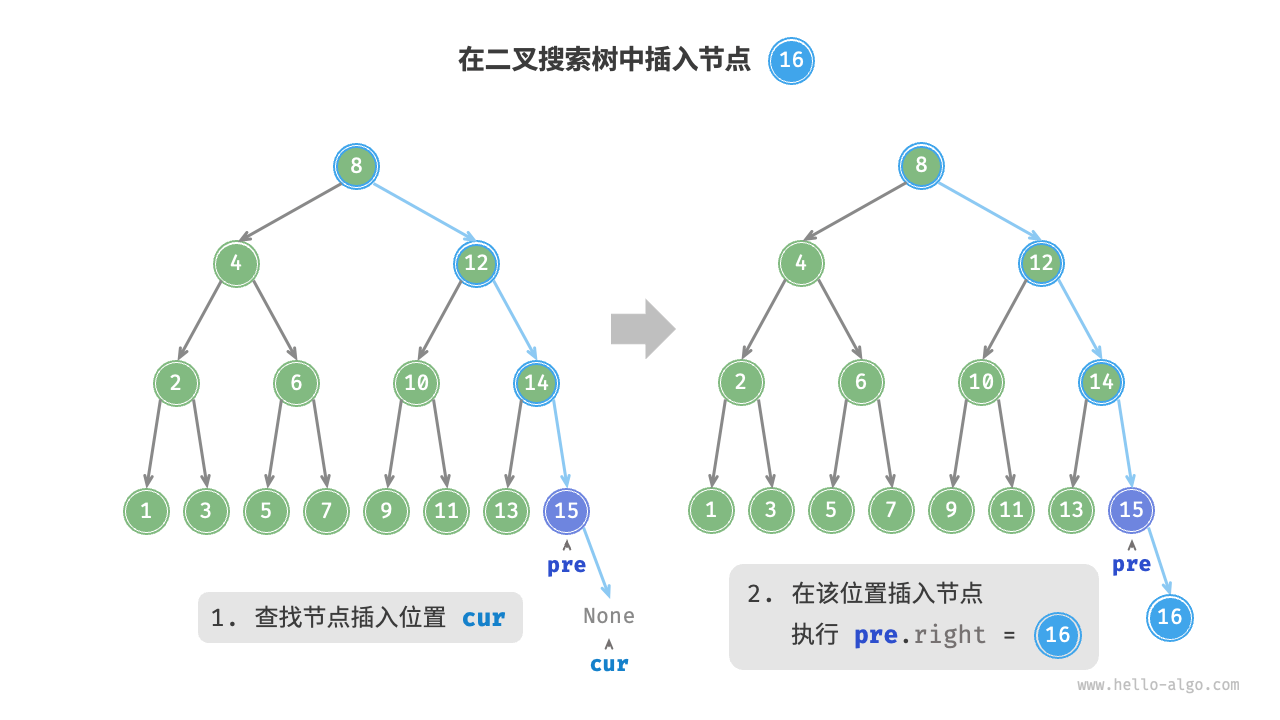
插入節點

插入節點時需要注意保持二叉搜索樹“左子樹 < 根節點 < 右子樹”的性質

1. 需要查詢插入位置：和查詢操作類似，從根節點觸發，直到葉節點（遍歷至 None ）時跳出循環。
2. 在該位置插入節點：初始化節點 num ，將該節點置于 None 的位置。

插入時需要注意：

• 二叉搜索樹不允許存在重復節點，否則將違反其定義。因此，若待插入節點在樹中已存在，則不執行插入，直接返回。

刪除節點

刪除節點需要區分三種情況，分別是節點的度為0/1/2時，進行的操作是不同的

• 度為0時，節點是葉節點，直接刪除
• 度為1時，該節點只有一個葉節點（高度為1），將待刪除節點替換為其子節點即可。
• 當待刪除節點的度為 2 時，我們無法直接刪除它，而需要使用一個節點替換該節點。由于要保持二叉搜索樹“左子樹 < 根節點 < 右子樹”的性質，因此這個節點可以是右子樹的最小節點或左子樹的最大節點。

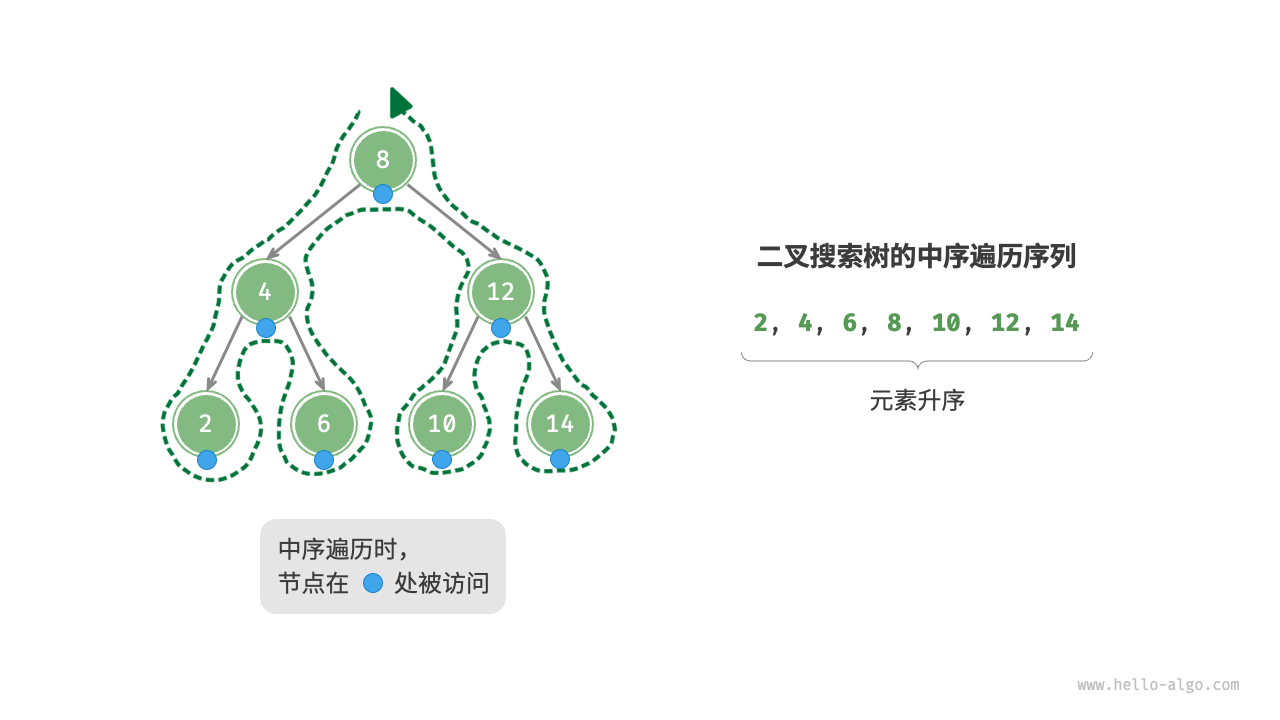
中序遍歷

由于二叉搜索樹的特性，中序遍歷遵循“左 → 根 → 右”的遍歷順序，而二叉搜索樹滿足“左子節點 < 根節點 < 右子節點”的大小關系。從而得出一個重要性質：二叉搜索樹的中序遍歷序列是升序的。

利用中序遍歷升序的性質，我們在二叉搜索樹中獲取有序數據僅需 O(n) 時間，無須進行額外的排序操作，非常高效。

2.4.4.2 搜索二叉樹的效率

對比無序數組和二叉搜索樹。

	無序數組	二叉搜索樹
查找元素	O(n)	O(log?n)
插入元素	O(1)	O(log?n)
刪除元素	O(n)	O(log?n)

• 二叉搜索樹的各項操作的時間復雜度都是對數階，具有穩定且高效的性能。可以得出二叉搜索樹是“平衡”的（理想狀態下
• 比較之下，二叉搜索樹在查詢和刪除元素時有較大優勢。
• 只有在高頻添加、低頻查找刪除數據的場景下，數組比二叉搜索樹的效率更高。.
• 如果我們在二叉搜索樹中不斷地插入和刪除節點，各種操作的時間復雜度也會退化為 O(n) 。

2.4.4.3 二叉搜索樹常見應用

• 用作系統中的多級索引，實現高效的查找、插入、刪除操作。
• 作為某些搜索算法的底層數據結構。
• 用于存儲數據流，以保持其有序狀態。

由于劣化的現象存在，所以在實際業務場景中是比較少見的。

為了解決二叉搜索樹會劣化的問題，后續基于二叉搜索樹給出了更優的算法

• 比如平衡二叉樹（AVL樹），通過一系列操作，確保在持續添加和刪除節點后，AVL 樹不會退化。AVL 樹?
• 還有非常出名的紅黑樹——自平衡的二叉查找樹具體可以看看文章

2.5 堆