操作環境:
MATLAB 2022a
1、算法描述
開普勒優化算法(Kepler Optimization Algorithm, KOA)是一個虛構的、靈感來自天文學的優化算法,它借鑒了開普勒行星運動定律的概念來設計。在這個構想中,算法模仿行星圍繞太陽的軌道運動來探索解空間,以尋找最優解。此算法的設計靈感來源于自然界的規律,特別是開普勒定律對行星運動的描述。在詳細介紹這個算法之前,先簡要回顧一下開普勒的三大定律:
-
第一定律(橢圓軌道定律):每個行星繞太陽旋轉的軌道都是橢圓形的,太陽位于橢圓的一個焦點上。
-
第二定律(等面積定律):連接行星和太陽的線段在相同時間內覆蓋的面積相等。
-
第三定律(調和定律):行星繞太陽公轉的周期的平方與其軌道半長軸的立方成正比。
基于上述定律,開普勒優化算法構建了一個模擬的太陽系,其中待優化問題的潛在解被視為行星,而當前最優解則是太陽。接下來,我們將詳細探討算法的主要組成部分、運作機制以及其在實際問題中的應用。
算法組成
初始化:在解空間內隨機生成一組解,這些解代表行星,每個行星具有其位置和速度。同時,從這些解中選擇一個當前最優解作為太陽。
迭代過程:
-
行星運動:每個行星根據其速度和與太陽的相對位置進行移動。行星的運動軌跡旨在模仿開普勒定律描述的天體運動,尤其是等面積定律,確保搜索過程既廣泛又深入。
-
速度和位置更新:行星的速度和位置根據其與太陽的相對關系動態更新,以模擬行星繞太陽旋轉的物理行為。
-
評估和更新太陽位置:在每次迭代中,所有行星的適應度(即解的質量)被評估,最優的行星可能成為新的太陽,即當前最優解。
終止條件:算法運行直到滿足預定的停止條件,如達到最大迭代次數或解的質量不再顯著改善。
算法特點
全局搜索能力:通過模擬行星的廣泛運動,KOA具有在整個解空間內進行搜索的能力,有助于避免局部最優解。
自適應調整機制:行星的運動軌跡和速度根據與太陽的相對位置動態調整,使得算法能夠根據當前搜索情況自適應地調整探索策略。
平衡探索與開發:等面積定律的應用有助于算法在新的搜索區域(探索)和已知的優秀區域(開發)之間保持平衡。
應用領域
開普勒優化算法由于其獨特的搜索機制,適用于多種優化問題,包括但不限于:
-
工程設計優化:在工程設計中尋找最優參數配置。
-
機器學習和深度學習:自動調整模型參數以提高性能。
-
經濟學模型:尋找最優的經濟決策和資源分配方案。
-
物流優化:優化貨物配送路線,減少成本和時間。
結論
開普勒優化算法將天文學原理與優化理論結合起來,提供了一種新穎的全局優化方法。通過模擬行星圍繞太陽的運動,它能夠有效地探索解空間,尋找到問題的最優解。雖然這里描述的KOA是一個理論上的構想,但它展示了自然現象與算法設計之間的交叉創新潛力,為解決復雜優化問題提供了新的思路和靈感。在未來,這種算法有可能被進一步研究和開發,以應對實際世界中的各種挑戰。
2、仿真結果演示

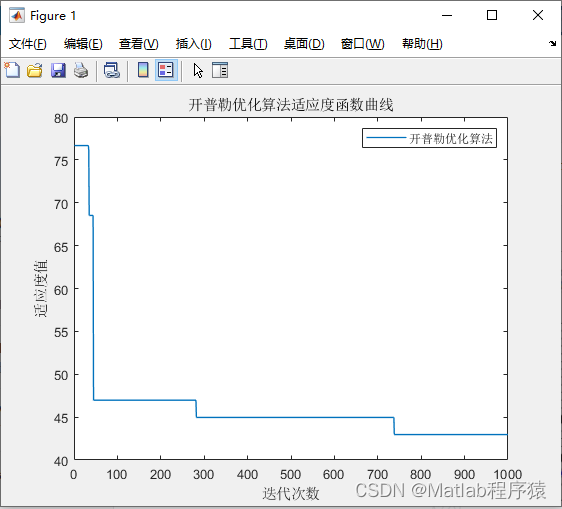
3、關鍵代碼展示
略
4、MATLAB?源碼獲取
? ? ? V
點擊下方名片

)



)





)
)

)




