C++_AVL樹

? ? ? ?

1、AVL的概念

2、平衡因子的調整概念

3、AVL樹的插入

3.1 調整平衡因子代碼實現

3.2 右旋操作

3.2 左旋操作?

3.3 雙旋-先右旋再左旋

3.4?雙旋-先左旋再右旋

3.5 旋轉操作的小結

4、AVL的驗證與實現

結語

前言：

????????在C++中，AVL樹是在二叉搜索樹的基礎上優化而來的，因為二叉搜索樹有一個缺陷，即如果插入的數據接近有序或者有序，那么二叉搜索樹就會變成一邊倒的結構，也就是”單支樹“，而”單支樹“查找數據效率就會變成和線性數據結構一樣的O(N)，失去了二叉樹本有的優勢。單支樹示意圖如下：

????????因此兩位俄羅斯的數學家G.M.Adelson-Velskii 和E.M.Landis在1962年推出了AVL樹的概念，AVL樹在每一次插入新節點的同時，會自動調整該樹的高度，即不會讓每個節點的左右子樹高度的絕對值不超過1，因此哪怕面對有序數據的插入也不會讓樹變成”單支樹“，可以使查找數據的效率始終保持在O(log N)。

1、AVL的概念

? ? ? ? AVL樹滿足以下兩個條件：

? ? ? ? 1、其每顆子樹都是AVL樹。

? ? ? ? 2、每個節點的左右子樹高度（可在節點中新加一個變量-平衡因子表示該節點的左右子樹高度）的絕對值不超過1。

? ? ? ? AVL樹示意圖如下：

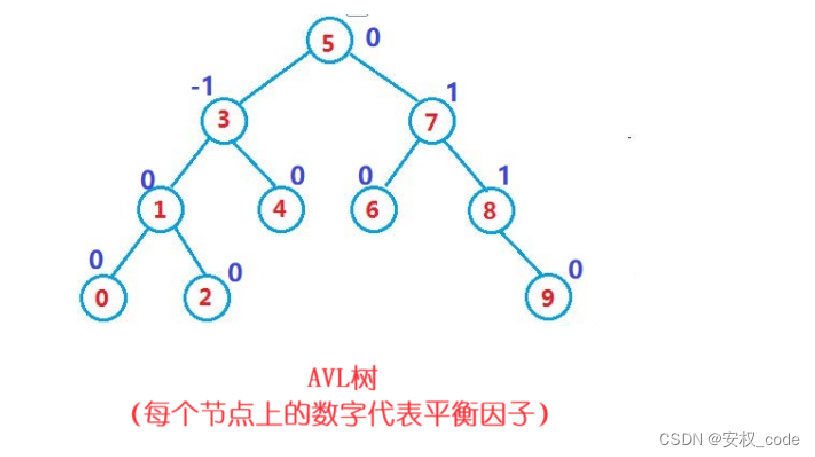
? ? ? ? 其中，-1表示該節點的左子樹高度高于右子樹高度1個單位，0表示該節點左右子樹高度一樣，1表示該節點的右子樹高度高于左子樹高度1個單位。轉換成公式：平衡因子=右子樹高度-左子樹高度。

2、平衡因子的調整概念

? ? ? ? AVL樹插入新節點的規則依舊是按照二叉搜索樹的規則，即左節點小于根結點，而右節點大于跟節點。只不過AVL新加入了平衡因子的概念，所以每次插入節點后，都需要對平衡因子做出調整，比如插入的節點為該子樹的根結點的右邊，則根結點的平衡因子需要+1。

? ? ? ? 此時，平衡因子的狀態就會出現三種情況：

? ? ? ? 1、插入節點后，根結點的平衡因子從正負1變為0，這種情況說明插入該節點后這棵樹子樹得到了平衡，無需做任何處理。

? ? ? ? 2、插入節點后，根結點的平衡因子從0變為1或-1，這種情況說明插入的節點破壞了該樹的原有平衡，雖然當前子樹的根結點的平衡因子的絕對值沒有超過1，但是該子樹的祖先節點的平衡因子的絕對值可能已經超過1了，所以需要”向上更新“，更改祖先節點的平衡因子。

? ? ? ? 3、插入節點后，該樹的某個節點的平衡因子的絕對值超過了1，則需要對該子樹進行旋轉處理。

? ? ? ? 具體示意圖如下：

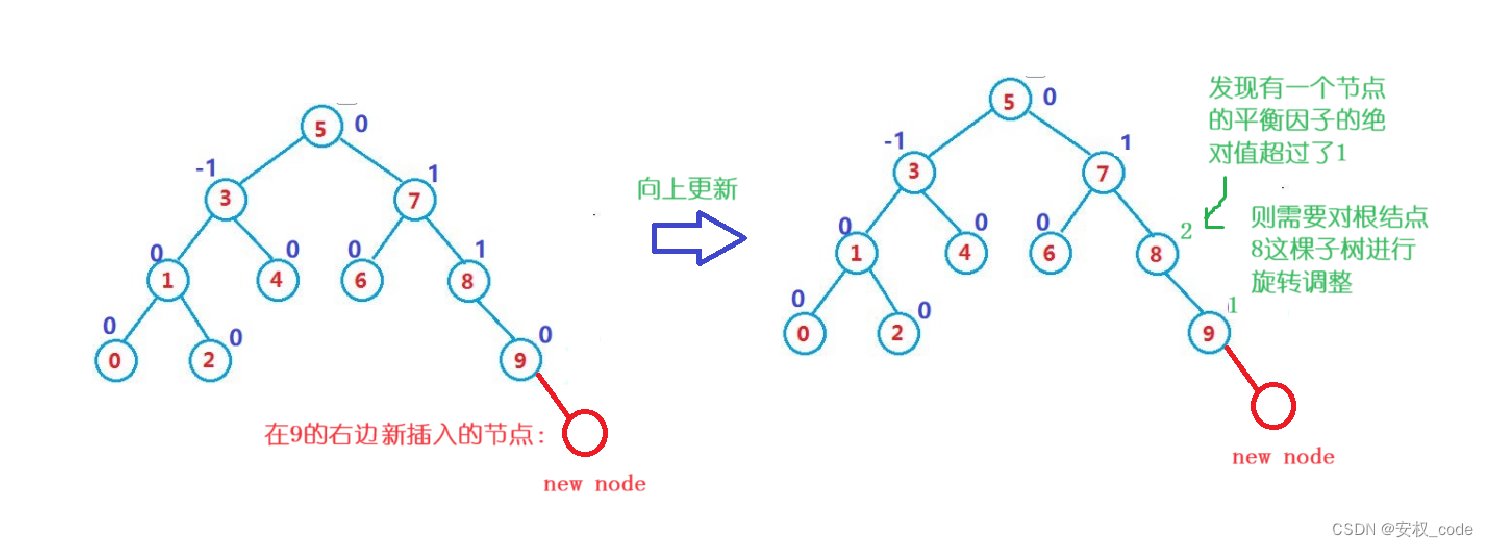
? ? ? ? 此時會發現，不管新插入的節點在9的右邊還是左邊，都會導致節點8的平衡因子變成2，因為對于9來說可能在哪邊插入節點都行，但是對于節點8來說，這兩個插入的節點都在8的右子樹，所以會導致8的平衡因子變成2。

? ? ? ? 在節點9的左邊插入節點的情況如下：

? ? ? ? ?只有在8的左邊插入節點，才不會引發旋轉調整，示意圖如下：

3、AVL樹的插入

? ? ? ? AVL樹的插入函數的實現可以分成三步：1、找到插入節點的合適位置。2、調整節點的平衡因子。3、對平衡因子異常的節點進行旋轉操作。

? ? ? ? 第一步是復用了二叉搜索樹的插入邏輯，即判斷要插入節點的值是否大于或小于根結點，若大于根結點則往右子樹遍歷，若小于根結點則往左子樹遍歷，直到找到節點指向的nullptr處，然后將插入節點與其父母節點相連接。

? ? ? ? 第二步調整平衡因子邏輯即上文敘述。

? ? ? ? 第三步進行的旋轉操作有：左旋、右旋、雙旋轉（即左右旋的結合），具體如下文。

3.1 調整平衡因子代碼實現

? ? ? ? 將上述的調整場景轉換為代碼：

#define _CRT_SECURE_NO_WARNINGS 1#include<iostream>
using namespace std;template<class K, class V>
class AVLTreeNode//節點
{AVLTreeNode<K, V>* _left;//指向左節點AVLTreeNode<K, V>* _right;//指向右節點AVLTreeNode<K, V>* _parent;//指向自己的父母節點pair<K, V> _kv;// 記錄數據用的pair類型int _bf; // 平衡因子AVLTreeNode(const pair<K, V>& kv):_left(nullptr), _right(nullptr), _parent(nullptr), _kv(kv), _bf(0){}
};template<class K, class V>
class AVLTree//AVL樹
{typedef AVLTreeNode<K, V> Node;
public:bool Insert(const pair<K, V>& kv){if (_root == nullptr){_root = new Node(kv);return true;}Node* parent = nullptr;Node* cur = _root;while (cur)//根據根節點大于左子樹，小于右子樹的邏輯找到合適的插入位置{if (cur->_kv.first < kv.first)//大的往右變量{parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first)//小的往左遍歷{parent = cur;cur = cur->_left;}else{return false;//AVL和二叉搜索樹一樣不允許有相同數據}}cur = new Node(kv);//找到合適位置后插入節點if (parent->_kv.first > kv.first){parent->_left = cur;//將該節點與父母節點相連接}else{parent->_right = cur;//將該節點與父母節點相連接}cur->_parent = parent;//將該節點與父母節點相連接// 更新平衡因子while (parent){if (cur == parent->_right){parent->_bf++;//插入的位置是節點的右邊，則平衡因子++}else{parent->_bf--;//插入的位置是節點的左邊，則平衡因子--}if (parent->_bf == 1 || parent->_bf == -1){// 繼續更新parent = parent->_parent;cur = cur->_parent;}else if (parent->_bf == 0)//等于0說明平衡了，則不處理{break;}else if (parent->_bf == 2 || parent->_bf == -2){// 需要旋轉處理 -- 1、讓這顆子樹平衡 2、降低這顆子樹的高度}else{assert(false);}}return true;}private:Node* _root = nullptr;
};

? ? ? ? 以上代碼已經實現了合適位置的查找和平衡因子的調整，插入函數的實現還差最后一步，即平衡因子等于2或者-2時旋轉操作的實現。

3.2 右旋操作

? ? ? ? 右旋操作是針對平衡因子為-2的場景，說明該節點的左子樹比右子樹要高，需要右旋降低左子樹的高度。并且旋轉完成后要更新平衡因子，具體操作示意圖如下：

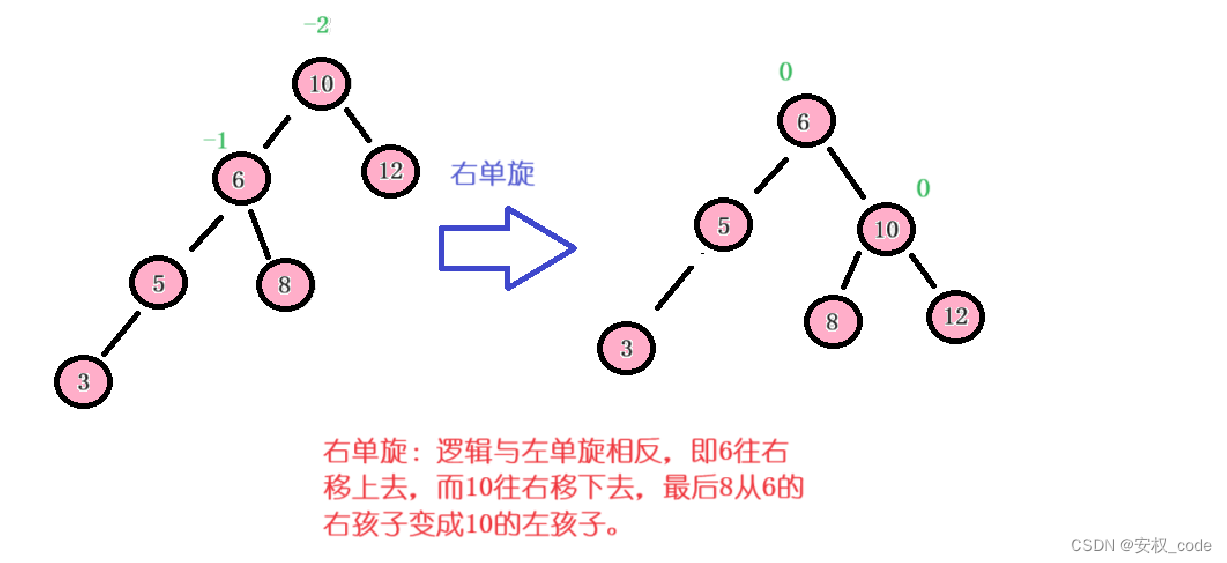
? ? ? ? 從結果可以看到，原本平衡因子是-2的節點經過旋轉操作之后變成了0。并且旋轉之后的節點與節點之間的邏輯依然是遵循小于根結點的在左邊，大于根節點的在右邊。

3.2 左旋操作?

? ? ? ? 左旋操作是針對平衡因子為2的場景，說明該節點的右子樹比左子樹要高，需要左旋降低右子樹的高度。并且旋轉完成后要更新平衡因子，具體操作示意圖如下：

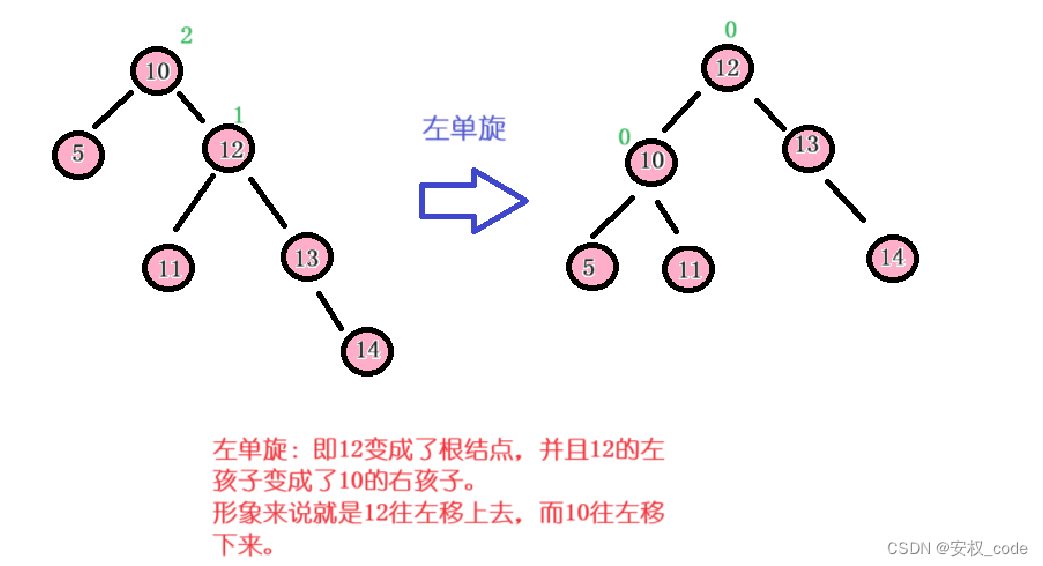
?????????從結果可以看到，原本平衡因子是2的節點經過旋轉操作之后變成了0。

? ? ? ? 無論是左旋還是右旋，都要注意兩個事項：

? ? ? ? 一、拿上述左旋舉例，節點12不一定存在左孩子，如果不存在左孩子則10的平衡因子是-1。

? ? ? ? 二、節點10不一定是根結點，可能是某個節點的左子樹或者右子樹，若10只是子樹，則旋轉后要將節點12與原先節點10的父母節點相連接。

3.3 雙旋-先右旋再左旋

? ? ? ? 從上述的例子可以發現，插入的節點都處于”邊緣“節點下，比如拿上述的左旋舉例，若插入的節點是插入到節點11下則如何調整呢？這時候就要用到雙選調整，比如上述的節點14作為節點11的孩子插入，則需要以節點12為一棵子樹，先進行右旋操作，然后再以根結點10進行左旋操作。

????????先右旋再左旋示意圖如下：

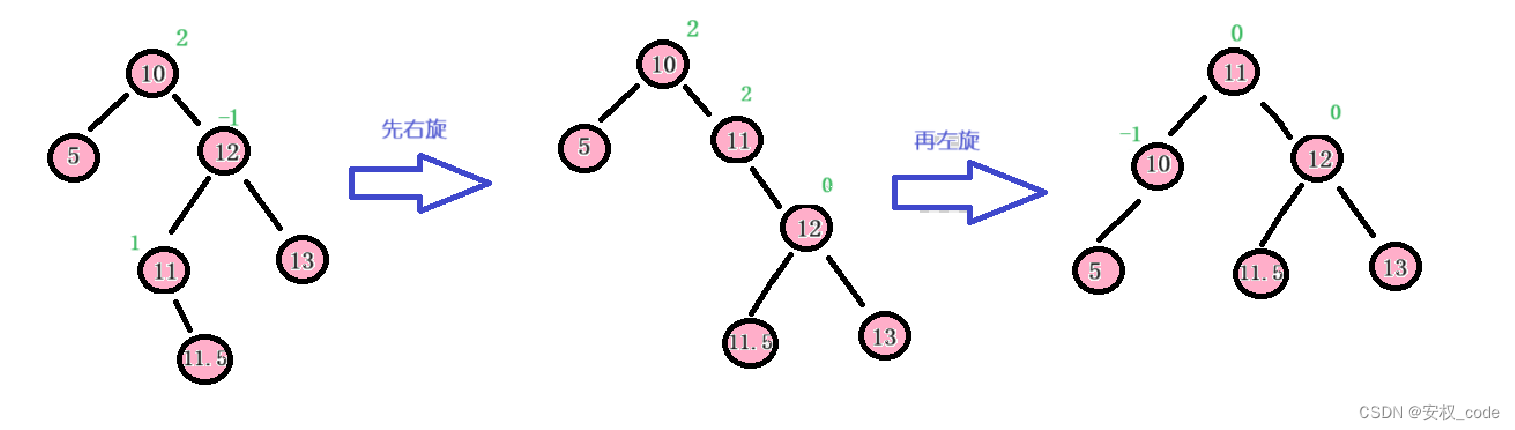
3.4?雙旋-先左旋再右旋

?????????用上述右旋的例子來進行說明，如果插入的節點是作為節點8的孩子節點，則需要先以節點6為子樹進行左旋，然后再以根結點10進行整棵樹的右旋。

? ? ? ? 先左旋再右旋的示意圖如下：

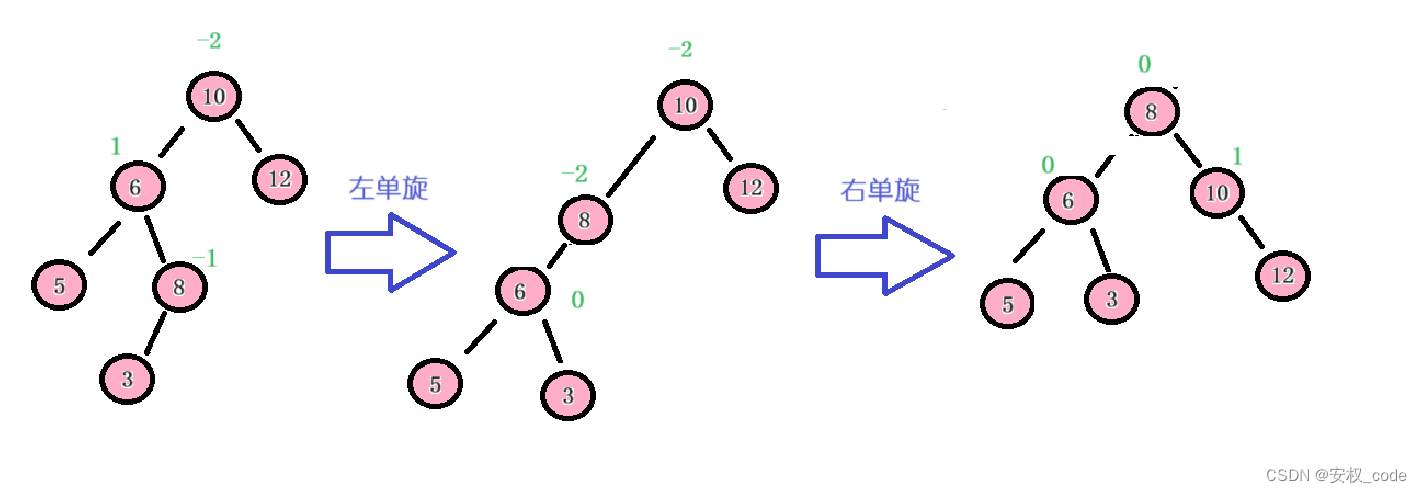
3.5 旋轉操作的小結

經過上述旋轉操作的細述，大致可以得出以下結論：

一、平衡因子為2的節點，說明該節點的右子樹高，因此只需要關注該節點的右孩子，其右孩子的平衡因子會有兩種情況：

? ? ? ? 1、該節點平衡因子若為1則只需要進行左旋轉即可。

? ? ? ? 2、該節點平衡因子若為-1則需要進行雙旋-先右旋再左旋。

二、平衡因子為-2的節點，說明該節點的左子樹高，因此只需要關注該節點的左孩子，其左孩子的平衡因子會有兩種情況：

? ? ? ? 1、該節點平衡因子若為1則需要進行雙旋-先左旋再右旋。

? ? ? ? 2、該節點平衡因子若為-1則只需要進行右旋轉即可。

? ? ? ? 從以上結論可以寫出旋轉代碼。

4、AVL的驗證與實現

? ? ? ? 判斷一棵樹是否為AVL樹的依據有兩點：1、中序遍歷的方式打印出來的是有序數據。2、每個節點的平衡因子的絕對值不超過2。

? ? ? ? AVL樹的實現代碼如下：?

#define _CRT_SECURE_NO_WARNINGS 1
#include <assert.h>
#include <time.h>
#include<iostream>
using namespace std;template<class K, class V>
struct AVLTreeNode
{AVLTreeNode<K, V>* _left;AVLTreeNode<K, V>* _right;AVLTreeNode<K, V>* _parent;pair<K, V> _kv;int _bf; // balance factorAVLTreeNode(const pair<K, V>& kv):_left(nullptr), _right(nullptr), _parent(nullptr), _kv(kv), _bf(0){}
};template<class K, class V>
class AVLTree
{typedef AVLTreeNode<K, V> Node;
public:bool Insert(const pair<K, V>& kv){if (_root == nullptr){_root = new Node(kv);return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(kv);if (parent->_kv.first > kv.first){parent->_left = cur;}else{parent->_right = cur;}cur->_parent = parent;// 更新平衡因子while (parent){if (cur == parent->_right){parent->_bf++;}else{parent->_bf--;}if (parent->_bf == 1 || parent->_bf == -1){parent = parent->_parent;cur = cur->_parent;}else if (parent->_bf == 0){break;}else if (parent->_bf == 2 || parent->_bf == -2){// 旋轉處理:1、讓這顆子樹平衡 2、降低這顆子樹的高度if (parent->_bf == 2 && cur->_bf == 1){RotateL(parent);}else if (parent->_bf == -2 && cur->_bf == -1){RotateR(parent);}else if (parent->_bf == -2 && cur->_bf == 1){RotateLR(parent);}else if (parent->_bf == 2 && cur->_bf == -1){RotateRL(parent);}else{assert(false);}break;}else{assert(false);}}return true;}void InOrder(){_InOrder(_root);cout << endl;}bool IsBalance(){return _IsBalance(_root);}int Height(){return _Height(_root);}private:int _Height(Node* root){if (root == NULL)return 0;int leftH = _Height(root->_left);int rightH = _Height(root->_right);return leftH > rightH ? leftH + 1 : rightH + 1;}bool _IsBalance(Node* root)//觀察平衡因子是否有問題{if (root == NULL){return true;}int leftH = _Height(root->_left);int rightH = _Height(root->_right);if (rightH - leftH != root->_bf){cout << root->_kv.first << "平衡因子異常" << endl;return false;}return abs(leftH - rightH) < 2&& _IsBalance(root->_left)&& _IsBalance(root->_right);}void RotateL(Node* parent)//左旋{Node* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;if (subRL)subRL->_parent = parent;Node* ppnode = parent->_parent;subR->_left = parent;parent->_parent = subR;if (ppnode == nullptr){_root = subR;_root->_parent = nullptr;}else{if (ppnode->_left == parent){ppnode->_left = subR;}else{ppnode->_right = subR;}subR->_parent = ppnode;}parent->_bf = subR->_bf = 0;}void RotateR(Node* parent)//右旋{Node* subL = parent->_left;Node* subLR = subL->_right;parent->_left = subLR;if (subLR)subLR->_parent = parent;Node* ppnode = parent->_parent;subL->_right = parent;parent->_parent = subL;if (parent == _root){_root = subL;_root->_parent = nullptr;}else{if (ppnode->_left == parent){ppnode->_left = subL;}else{ppnode->_right = subL;}subL->_parent = ppnode;}subL->_bf = parent->_bf = 0;}void RotateLR(Node* parent)//左右旋{Node* subL = parent->_left;Node* subLR = subL->_right;int bf = subLR->_bf;RotateL(parent->_left);RotateR(parent);if (bf == 1){parent->_bf = 0;subLR->_bf = 0;subL->_bf = -1;}else if (bf == -1){parent->_bf = 1;subLR->_bf = 0;subL->_bf = 0;}else if (bf == 0){parent->_bf = 0;subLR->_bf = 0;subL->_bf = 0;}else{assert(false);}}void RotateRL(Node* parent)//右左旋{Node* subR = parent->_right;Node* subRL = subR->_left;int bf = subRL->_bf;RotateR(parent->_right);RotateL(parent);if (bf == 1){subR->_bf = 0;parent->_bf = -1;subRL->_bf = 0;}else if (bf == -1){subR->_bf = 1;parent->_bf = 0;subRL->_bf = 0;}else if (bf == 0){subR->_bf = 0;parent->_bf = 0;subRL->_bf = 0;}else{assert(false);}}void _InOrder(Node* root)//中序遍歷AVL樹{if (root == nullptr){return;}_InOrder(root->_left);cout << root->_kv.first << " ";_InOrder(root->_right);}
private:Node* _root = nullptr;
};int main()
{int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 };AVLTree<int, int> t1;for (auto e : a){t1.Insert(make_pair(e, e));}t1.InOrder();cout << t1.IsBalance() << endl;return 0;
}