62. 不同路徑 - 力扣(LeetCode)
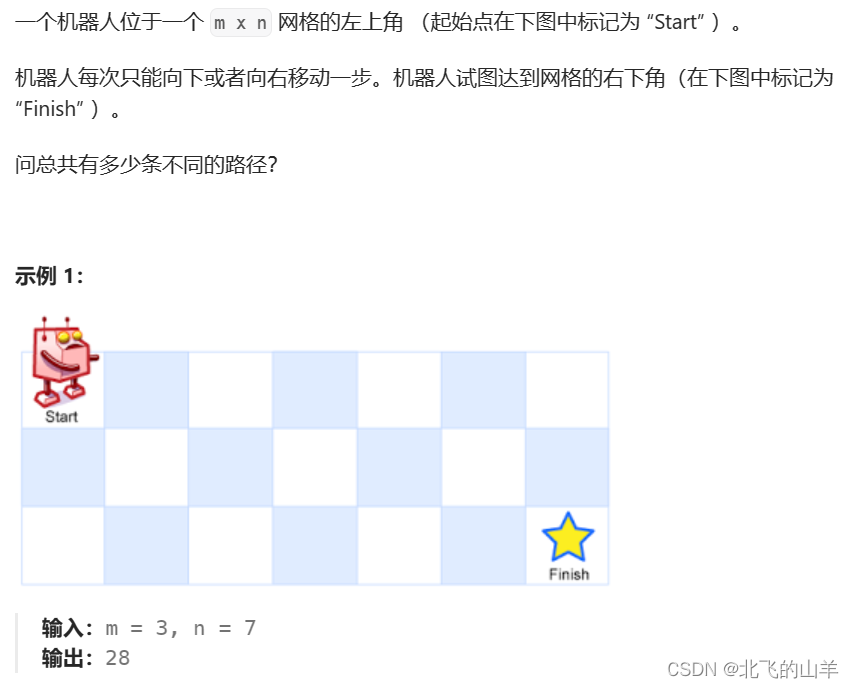
????????思路:選定一個網格為終點,走到這個網格的所有走法就是這個網格的上面一個網格的所有走法加上這個網格左邊一個網格的所有走法,然后做好初始化工作就行。?
class Solution {
public:int uniquePaths(int m, int n) {//dp表int arr[m][n];//特殊處理if(m == 1 || n == 1)return 1;//初始化for(int i = 0; i<m; i++){arr[i][0] = 1;}for(int i = 0; i<n; i++){arr[0][i] = 1;}//狀態轉移方程for(int i = 1; i<m; i++){for(int j = 1; j<n; j++){arr[i][j] = arr[i][j-1] + arr[i-1][j];}}return arr[m-1][n-1];}
};63. 不同路徑 II - 力扣(LeetCode)

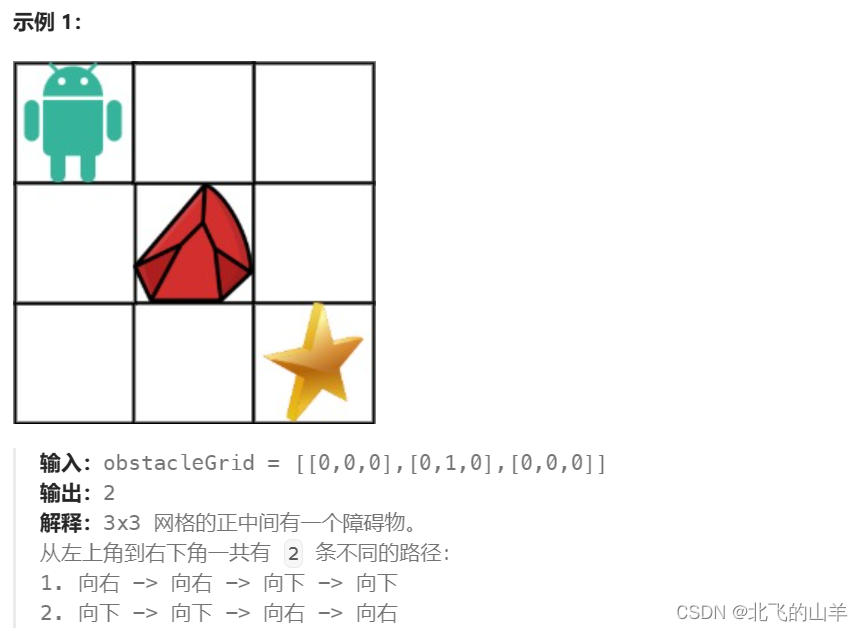
????????思路: 這道題可以看做事上面那道題的升級版,我的思路就是先將創建出來的dp表先全部初始化為0,在狀態轉移方程中,如果遇到障礙物,就保持dp表中障礙物位置的值仍為0,其余位置的值為它的上面加上它的左邊。這時有人可能就會有疑問了,如果一個位置的左邊或者是上面為障礙物不影響賦值嗎?答案是不影響的。因為障礙物位置的值就是0,加上跟沒加沒有區別,所以可以統一加上。
class Solution {
public:int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) { //dp表int m = obstacleGrid.size();int n = obstacleGrid[0].size();vector<vector<int>> dp(m, vector<int>(n));//初始化for(int i = 0; i<n; i++){if(obstacleGrid[0][i] == 0)dp[0][i] = 1;elsebreak;}for(int i = 0; i<m; i++){if(obstacleGrid[i][0] == 0)dp[i][0] = 1;elsebreak;}//狀態轉移方程for(int i= 1; i<m; i++){for(int j = 1; j<n; j++){if(obstacleGrid[i][j] != 1)dp[i][j] = dp[i-1][j] + dp[i][j-1];}}return dp[m-1][n-1];LCR 166. 珠寶的最高價值 - 力扣(LeetCode)

?????????思路:這題采用的方法略微跟上面兩題不同,這一題的dp表我多補了一行和一列,通過比較所在位置的上面一個位置和左邊一個位置誰大,加上值大的那個位置,只不過這種方法要注意兩個表之間下標的對應關系。
class Solution {
public:int jewelleryValue(vector<vector<int>>& frame) {//dp表int m = frame.size();int n = frame[0].size();vector<vector<int>> dp(m+1, vector<int>(n+1));//初始化+狀態轉移方程for(int i = 1; i<=m ;i++){for(int j = 1; j<=n; j++){if(dp[i-1][j] < dp[i][j-1]){dp[i][j] += frame[i-1][j-1]+dp[i][j-1];}else{dp[i][j] += frame[i-1][j-1] + dp[i-1][j];}}}return dp[m][n];}
};
)




)


)









