一、求值域的兩種基本思路
1、根據函數圖像和定義域求出值域。
難點:畫出函數圖像
2、研究函數單調性和定義域求出值域。
二、函數圖像畫法
高中所學的分式函數,基本由反比例函數平移得到。
復雜分式函數圖像畫法的兩個要點:
a、找垂直、水平漸近線
垂直漸近線:分母等于0時,x的取值
水平漸近線:x取無窮大的時候,y的極限值
b、代值定象限
當你不確定圖像是1,3象限,還是2,4象限的時候,代入特殊值即可判斷。
1、反比例函數
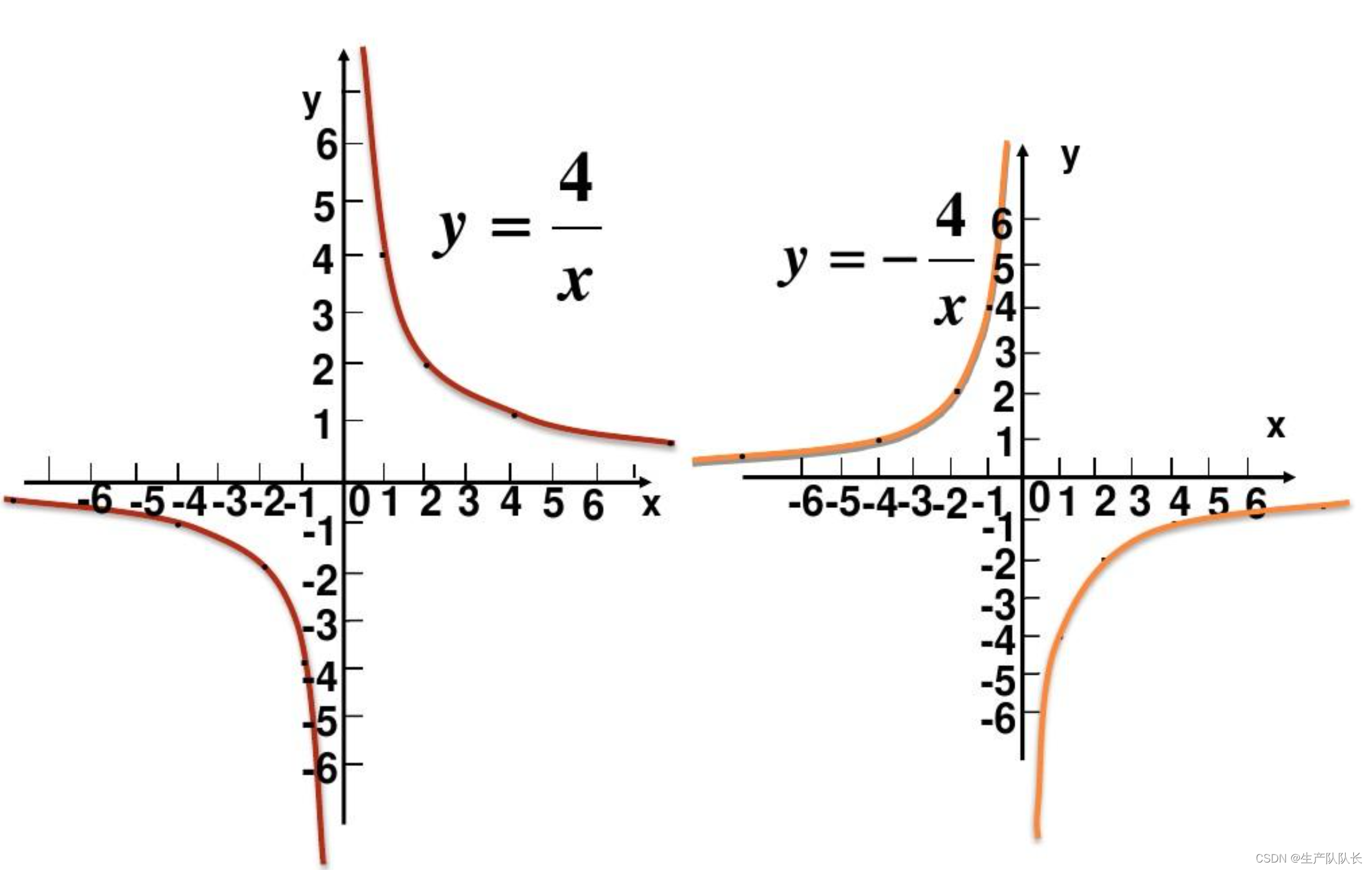
2、對勾函數
一個正比例函數 加 一個分式函數
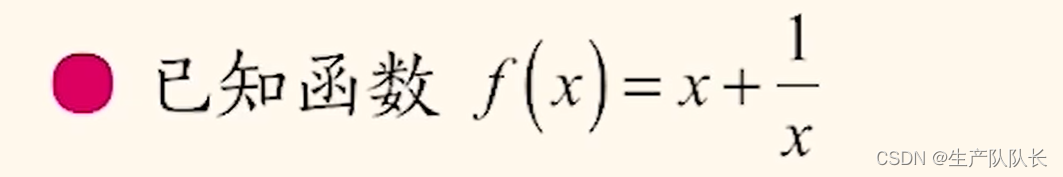
第一步
分別畫出y=x和y=1/x的圖像
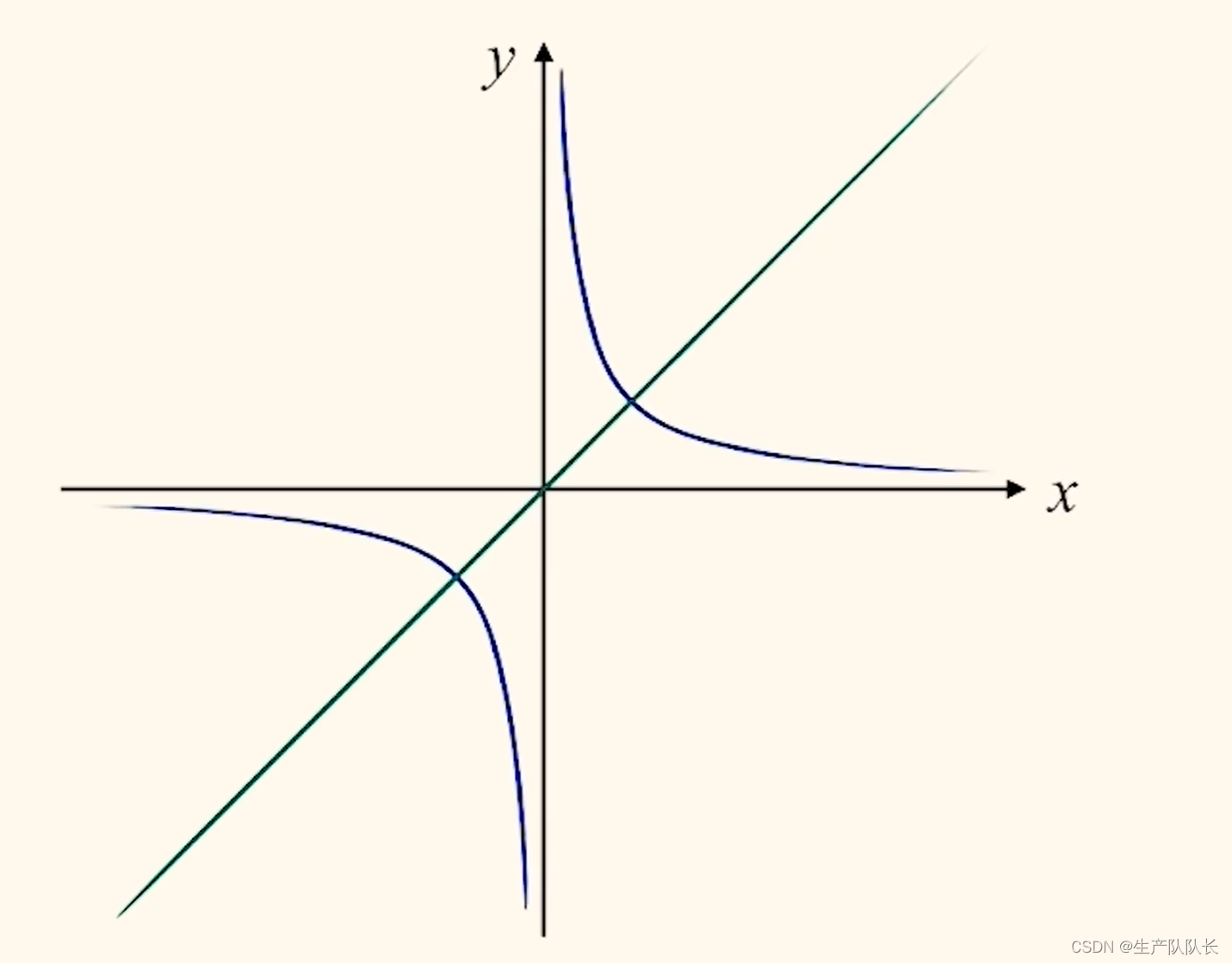
第二步
合并函數圖像
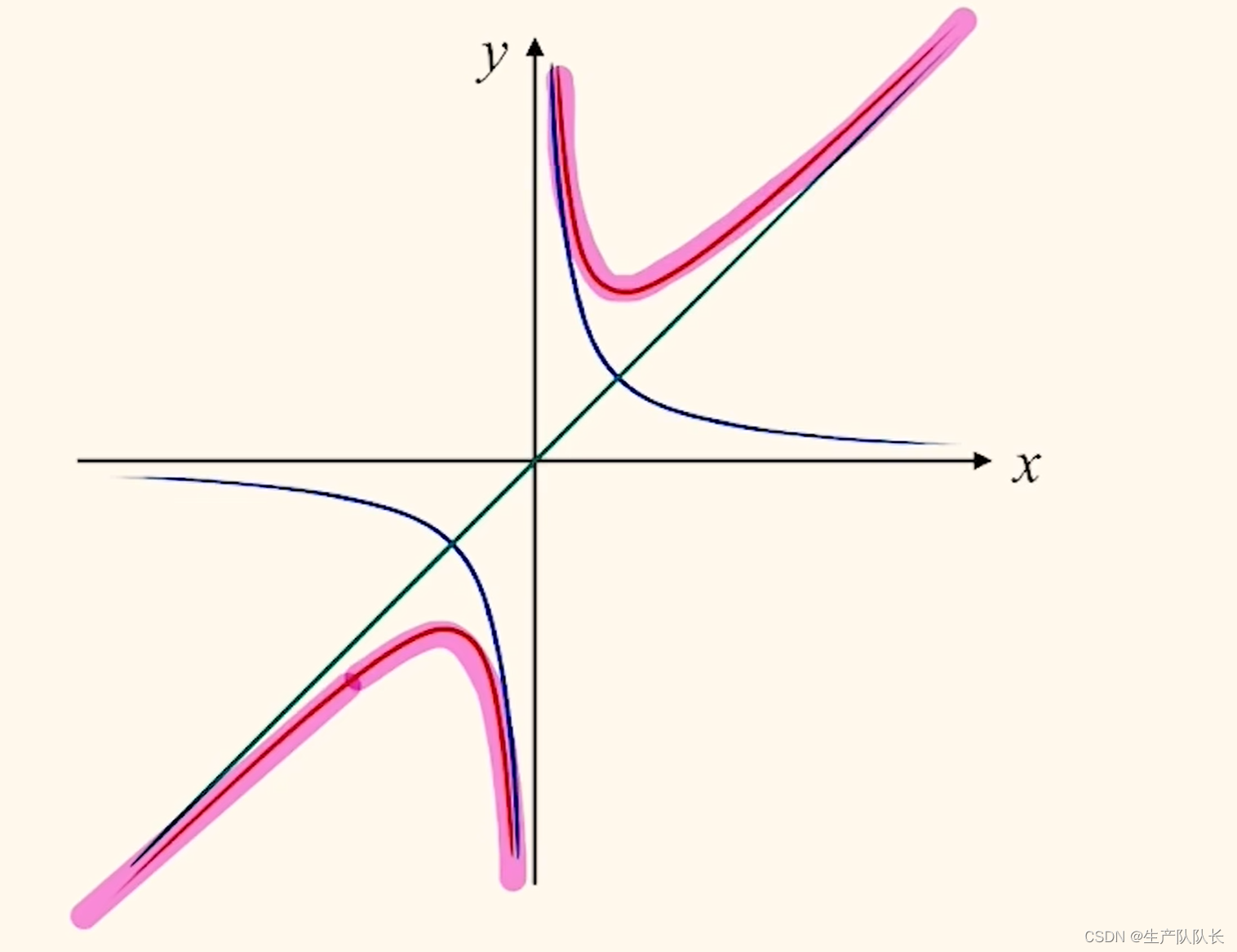
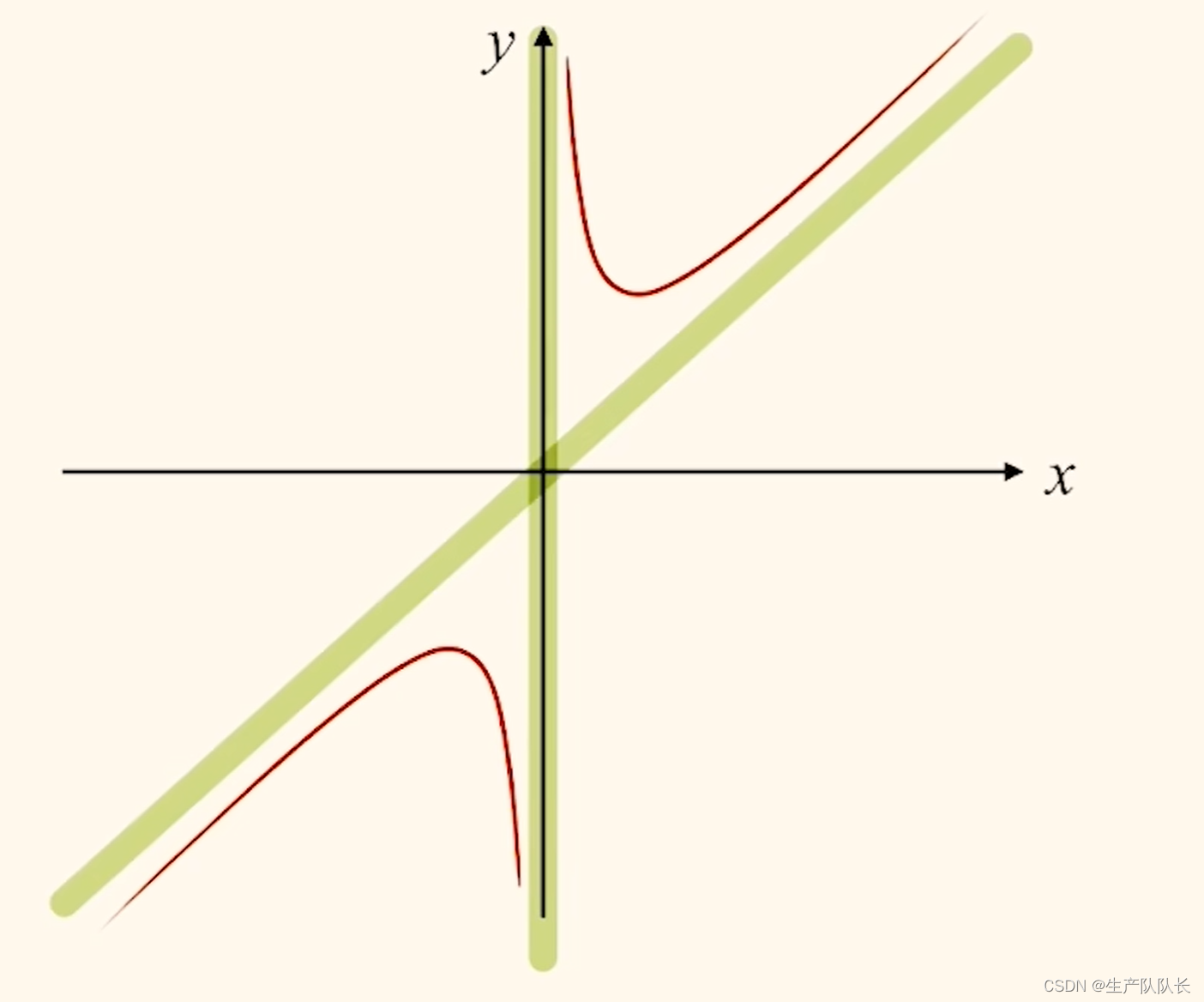
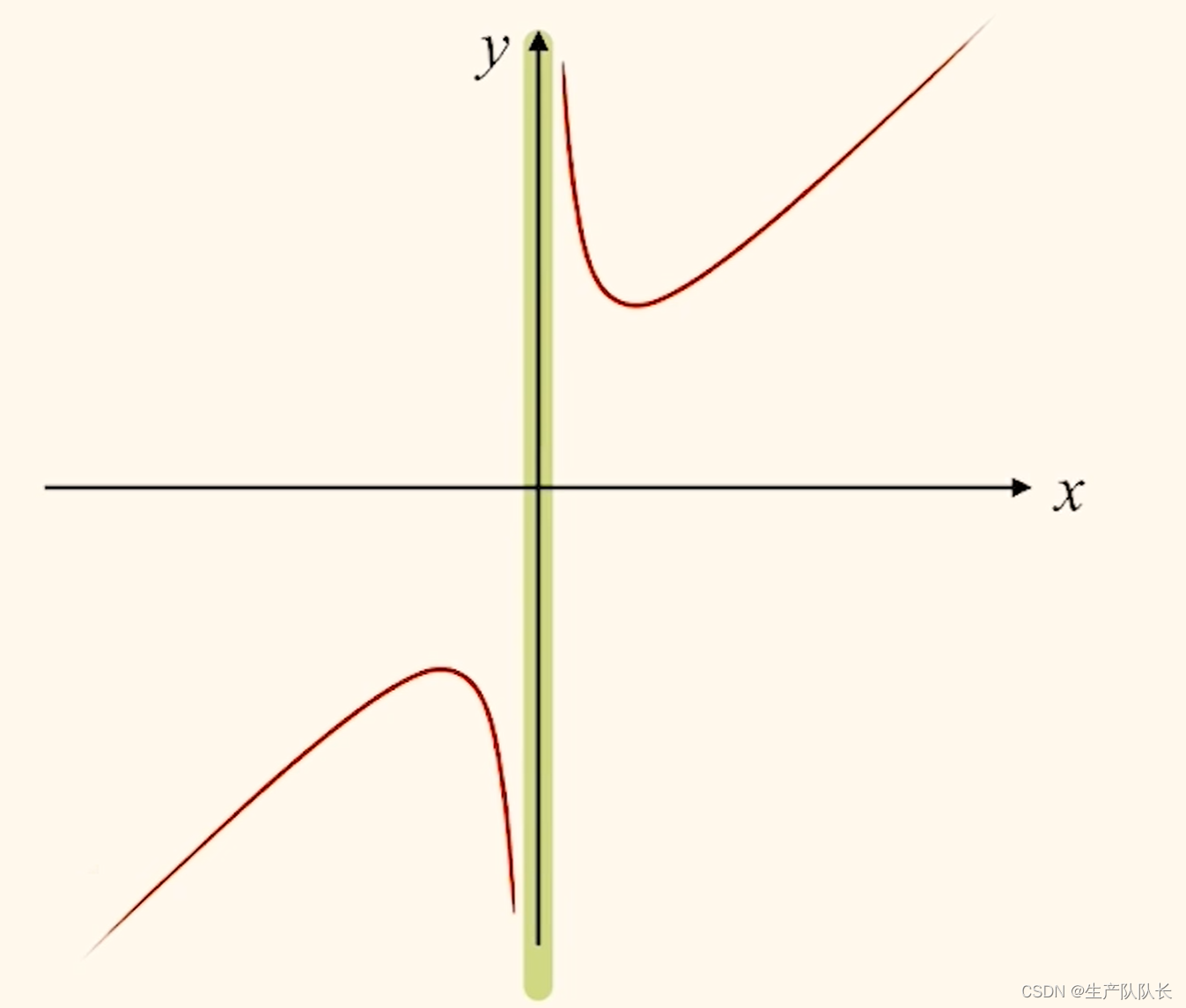
可以看出,該圖像的兩條漸近線是,x=0和y=x
第三步
求頂點
根據基本不等式,可以求出第一象限的最小值。
根據圖像的中心對稱性,求出第三象限的最大值。
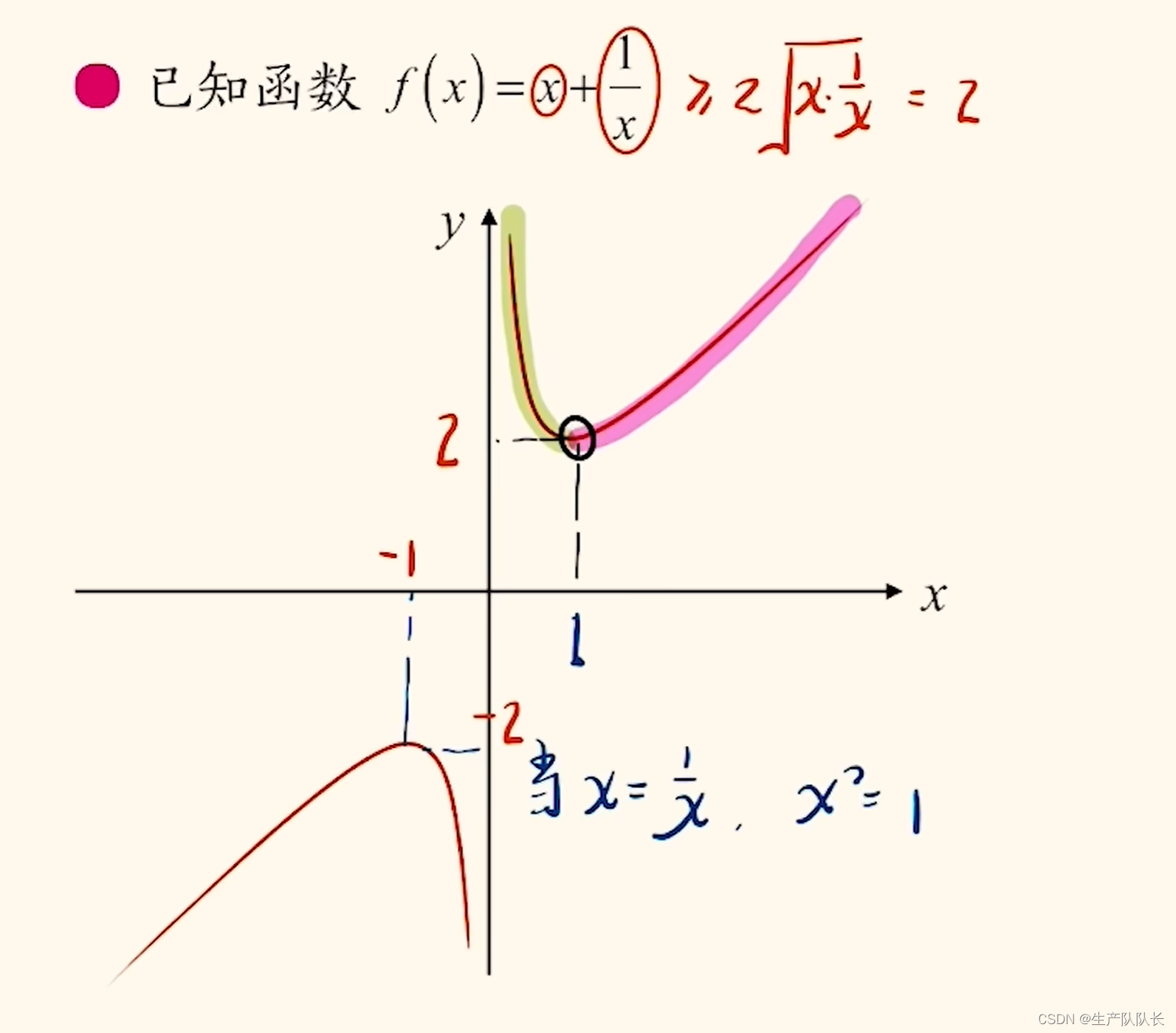
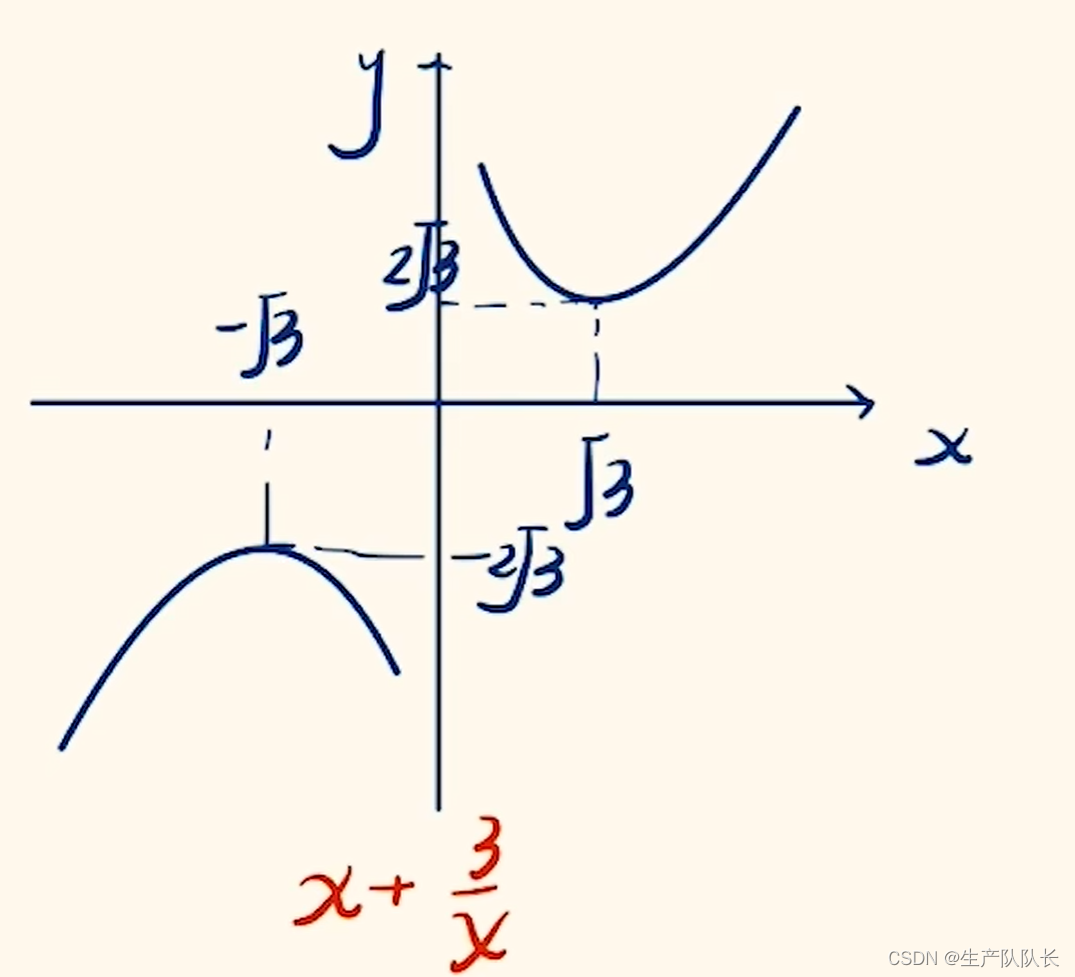
3、雙刀函數
一個正比例函數 減 一個分式函數
雙刀函數圖像的畫法和對勾函數圖像畫法過程相似。
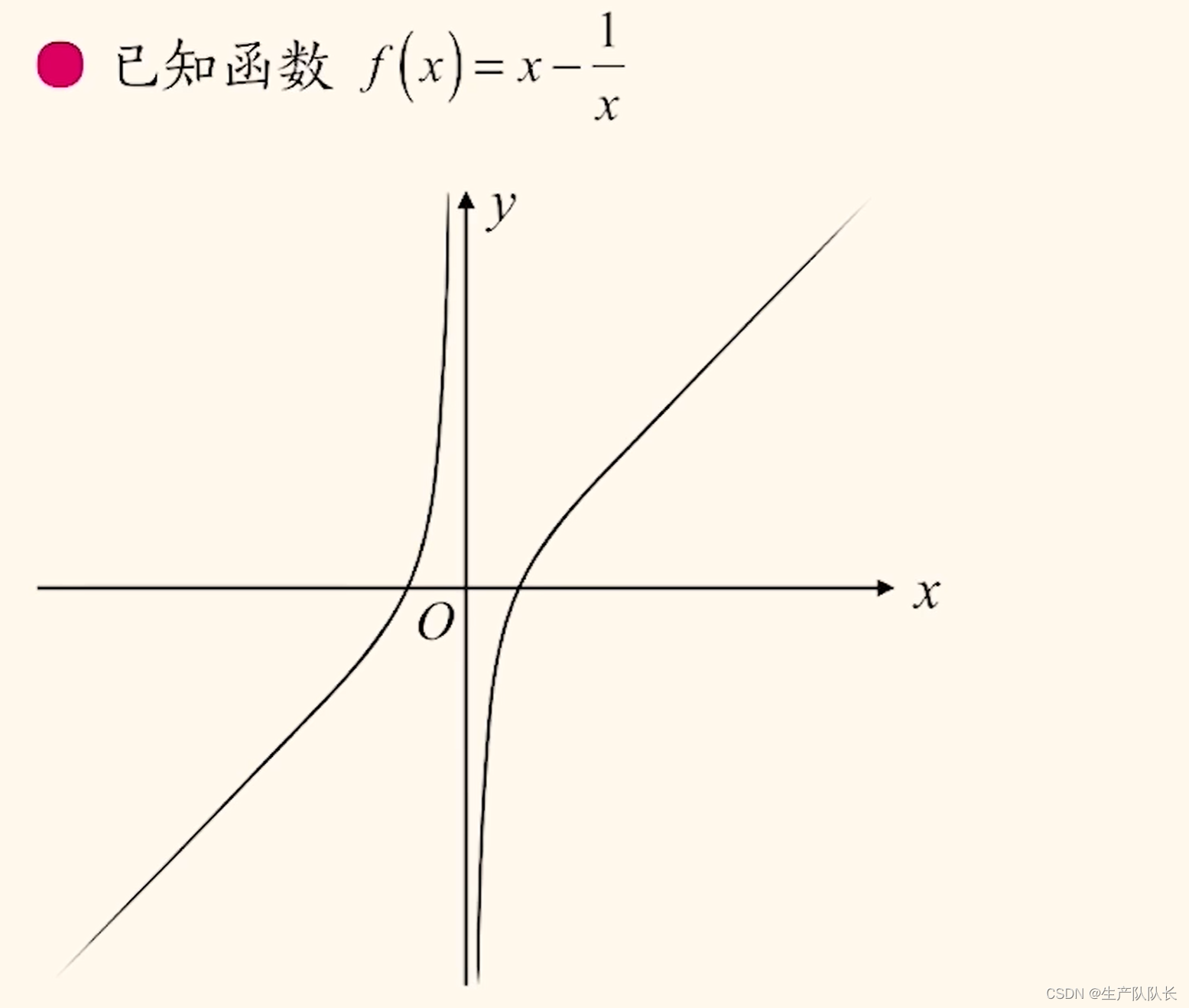
三、分式函數求值域
1、一次比一次的分式函數
分母和分子中,x的次數都是1次的情況
例題:
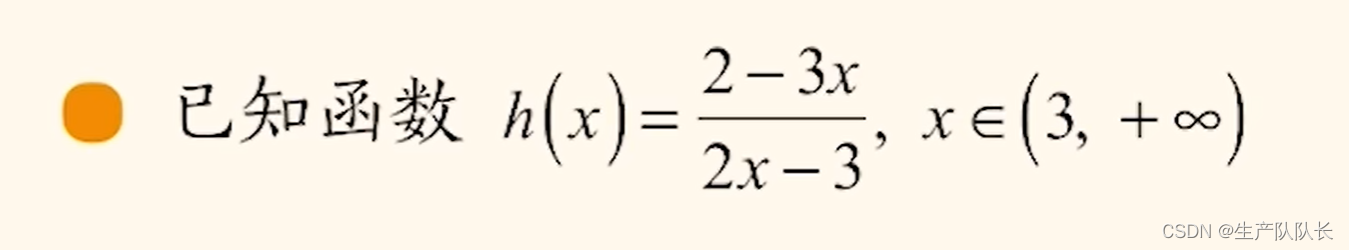
畫圖:
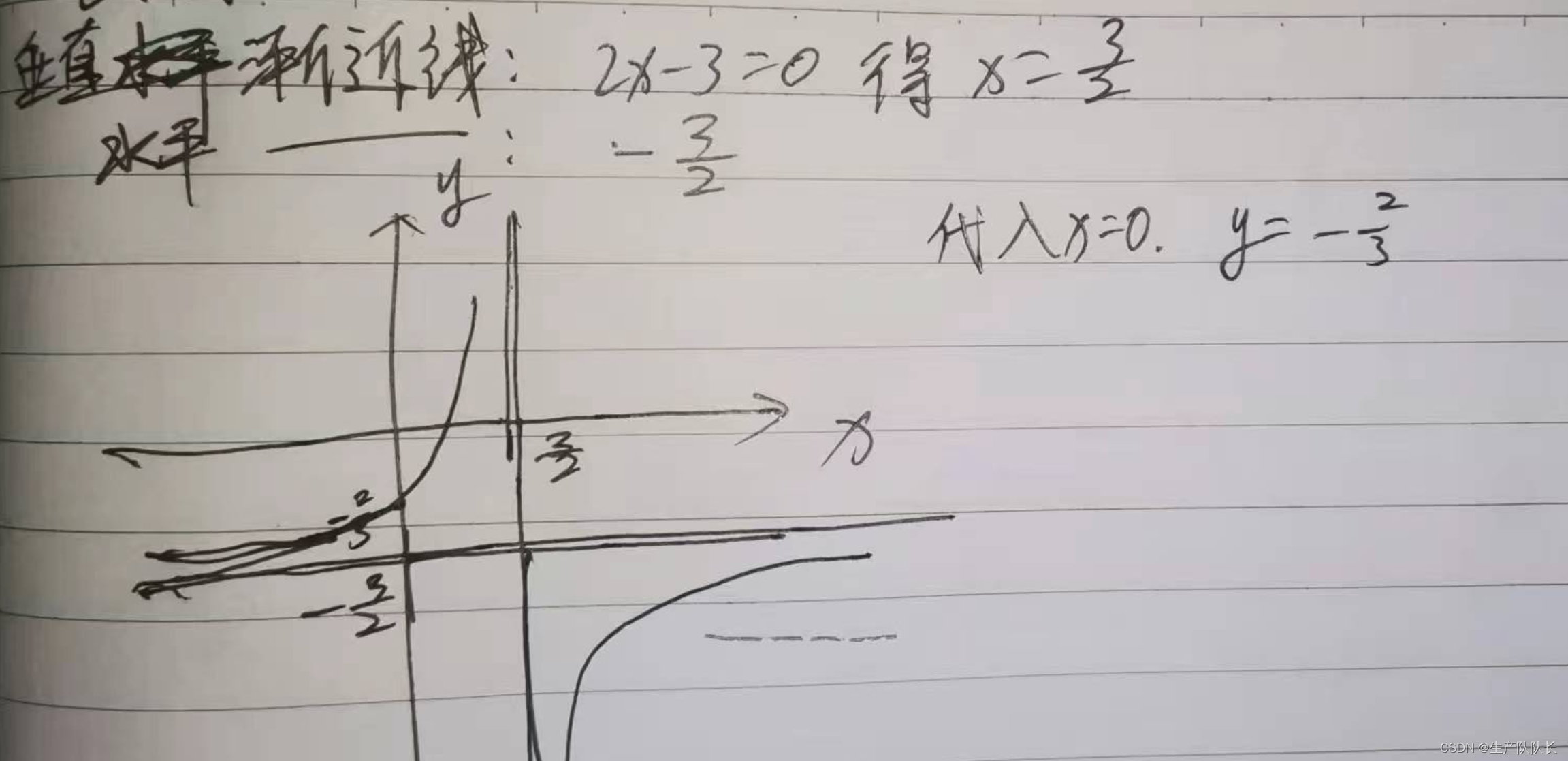
求值域:
根據圖像,值域一目了然。
2、二次比一次的分式函數
分子中x的次數是2次,分母中x的次數是1次的情況
例題1:
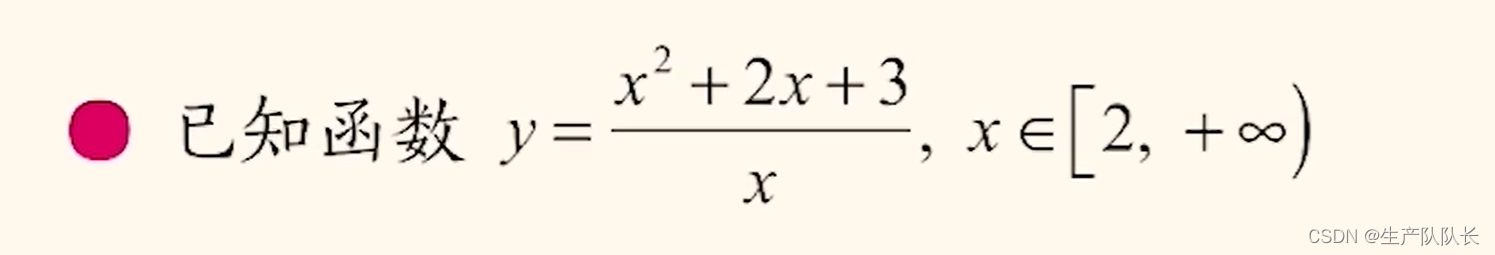
畫圖:
1、拆分子
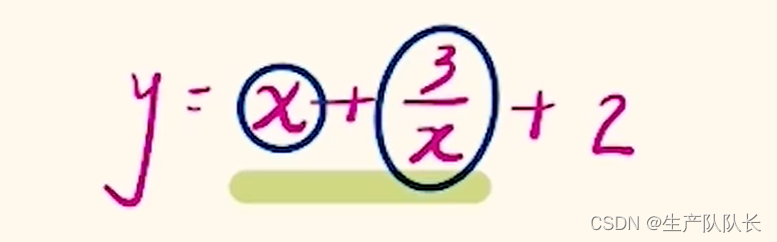
2、畫圖
可以發現,這個函數圖像是一個對勾函數,向上平移兩個單位得到的圖像。
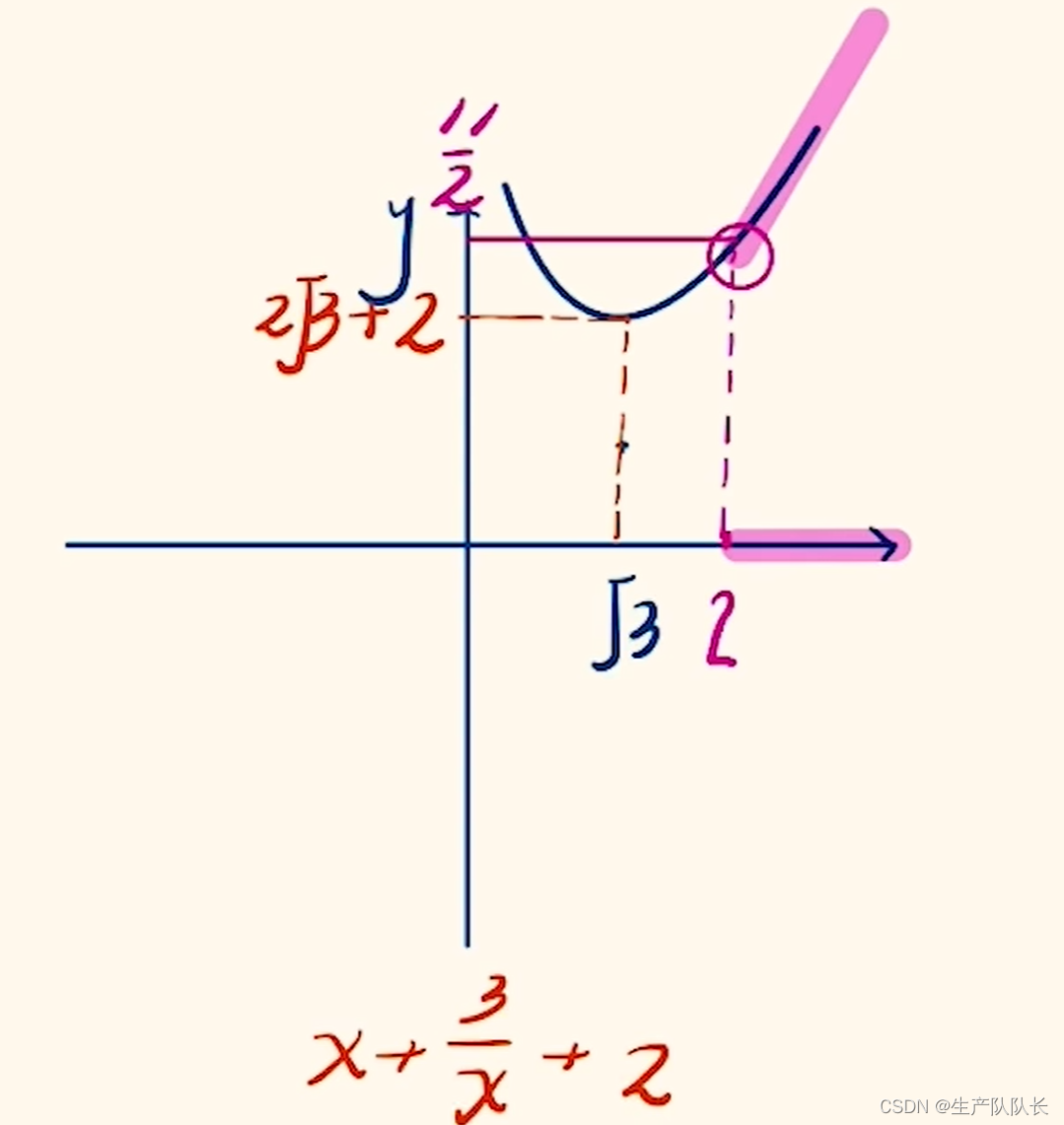
求值域:
根據圖像,一目了然
例題2:
這種情況對分母換元即可轉化為例題1的情況,進行畫圖求解即可。
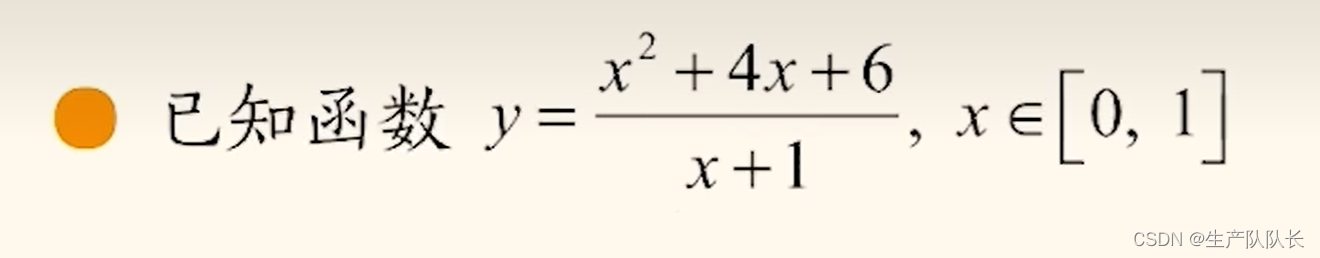
3、一次比二次的分式函數
分子中x的次數是1次,分母中x的次數是2次的情況
例題:
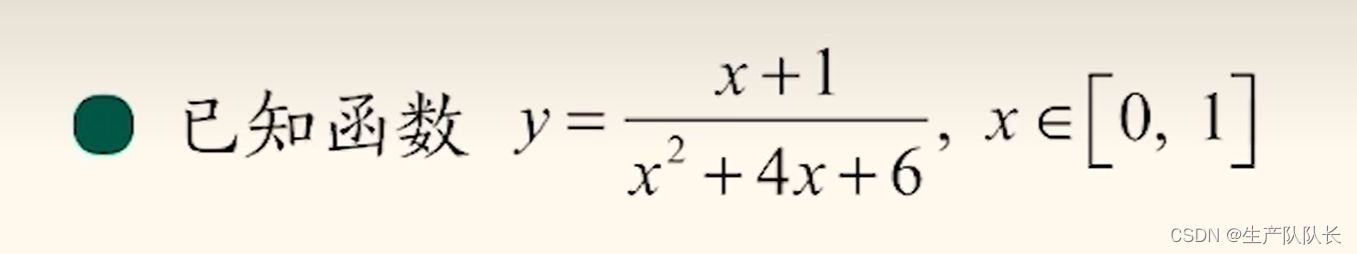
畫圖:
1、對一次項式分子換元
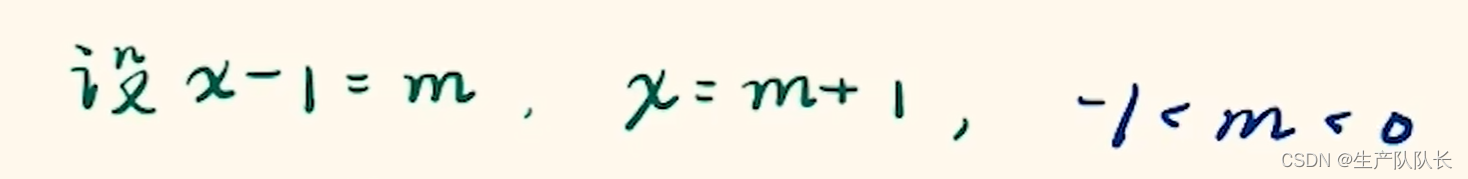
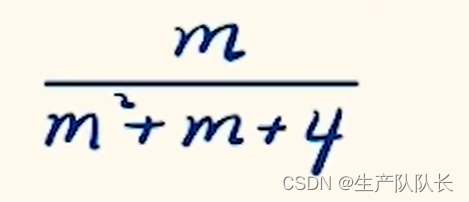
2、上下同除以分子
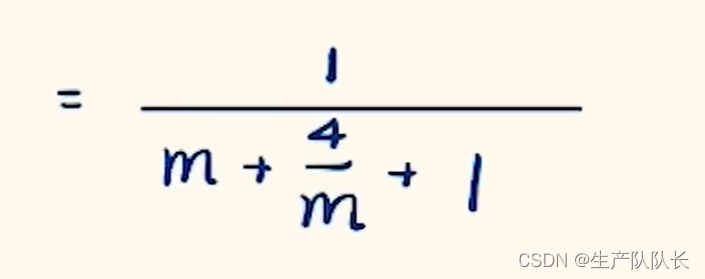
3、對分母畫圖
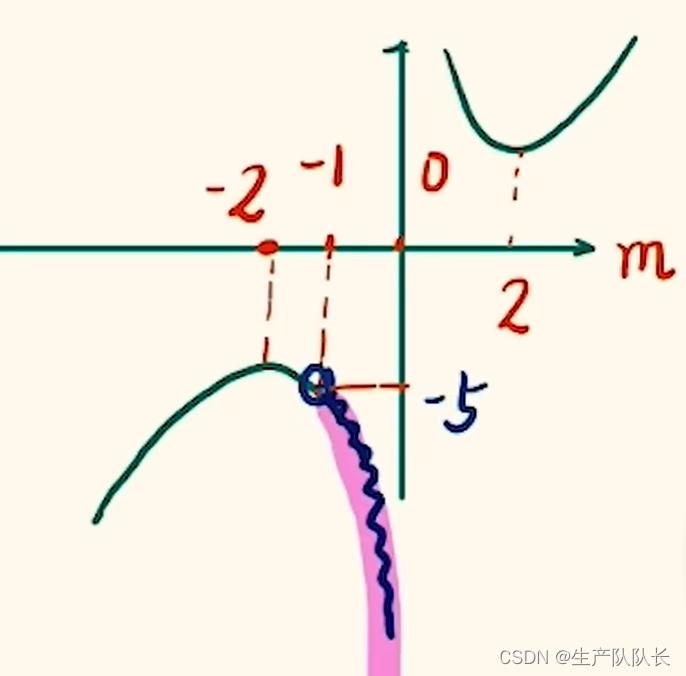
求值域:
求出分母的值域,從而求出分式的值域
4、二次比二次的分式函數
分子中x的次數是2次,分母中x的次數是2次的情況
例題:
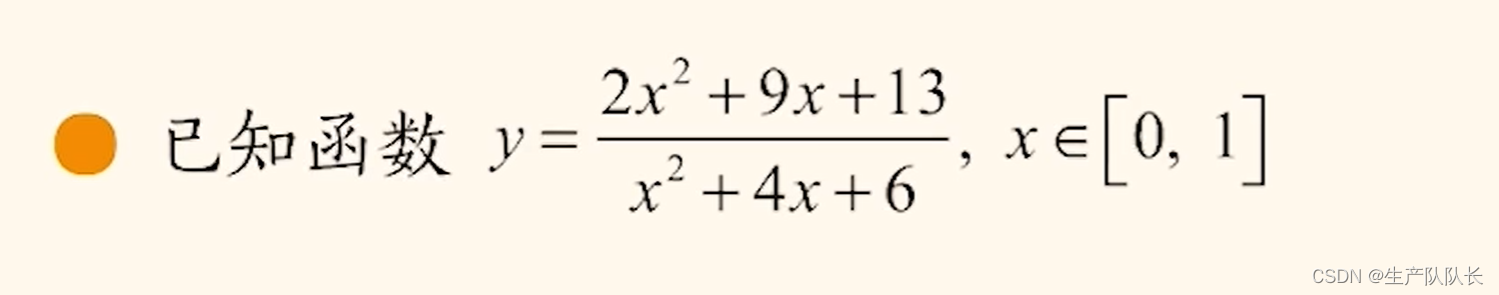
解題:
1、將分子湊成分母的倍數
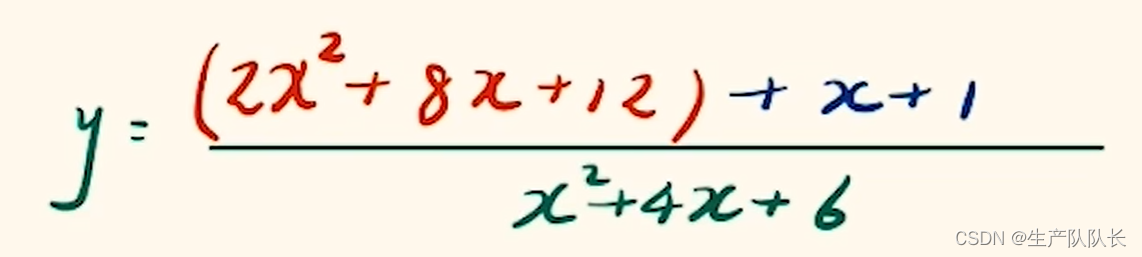
2、拆分子
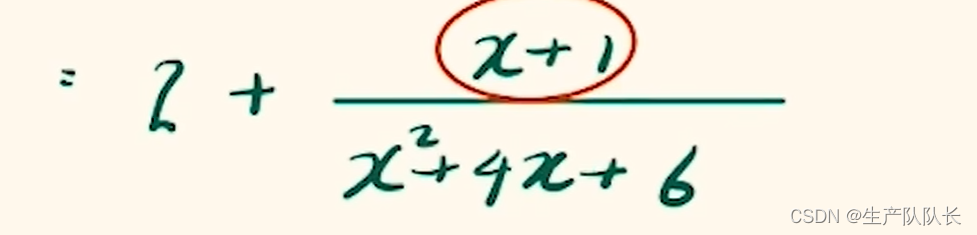
3、按照一次比二次的分式函數的解法求解即可。








)










