一、每日一題 - 填充

詳細題解

s = input()  # 輸入字符串
n = len(s)  # 定義字符的長度
judge = ["00", "11", "0?", "1?", "?0", "?1", "??"]
# 把所有的情況一一列舉出來
count = 0  # 設置計數器
i = 1  # 設置循環條件索引值
while i < n:if s[i-1:i+1] in judge:  # 在循環中將字符串遍歷進行判斷count += 1  # 如果符合計數器 + 1i += 2  # 并將索引值向后移動2個else:i += 1 # 不符合條件索引值向后移1個print(count)  # 最后打印出結果

?我覺得最難的在于不糾結？到底是0還是1，而是直接把他看成數字去跟已知情況進行判斷。我一直在糾結？到底應該什么時候是1，什么時候是0，把自己的思路的限制住了。

二、堆排序

預備基礎知識 - 樹

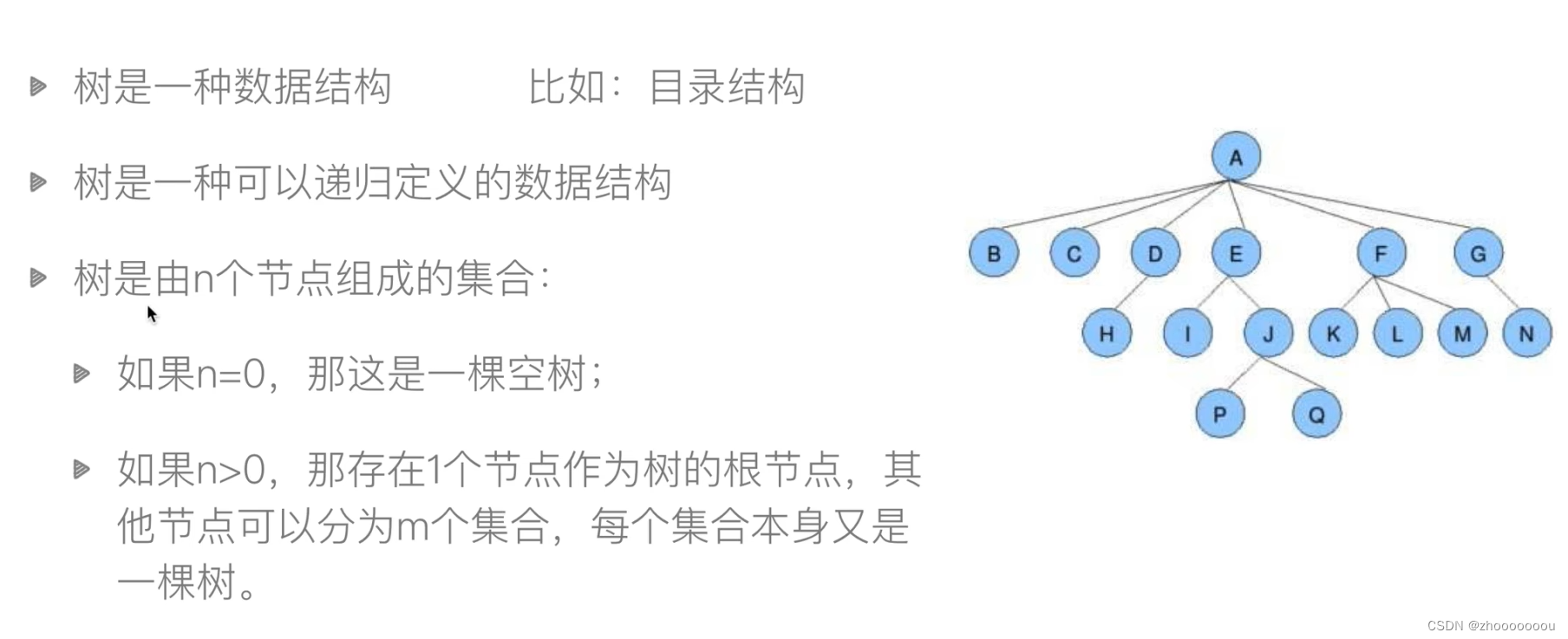
?一些基本知識：

根節點：每棵樹最上面的單獨的一個節點，如上圖A為根節點。

葉子節點：每棵樹中最末梢的，不再有分支的節點。如上圖B,C,H,I,P,Q,K,L,M,N為葉子節點。

樹的深度(高度)：層數是幾，深度(高度)是幾。如上圖樹的深度(高度)是4，因為有4層。

節點的度：某個分叉的節點分了幾個叉，節點的度就是幾。如上圖E的度為2，F的度為3.

樹的度： 節點的度中最大的數，就是樹的度。如上圖節點的度最大為A分了6個叉，所以樹的度為6

孩子節點/父節點：掛在某個節點下面，稱為這個節點的孩子節點，某個節點稱為父節點。如上圖中E是父節點，I,J是孩子節點。

子樹：在樹中單獨拎出來一些節點還能組成樹的，稱為這棵樹的子樹。如上圖中E,F,G單獨拎出來后還是一棵樹，故能稱為是A這棵樹的子樹。

這些都是按照我理解的概念寫出來的，可能不完善也不是很清楚，最好還是參考課本上的定義概念。

二叉樹

?滿二叉樹、完全二叉樹

?

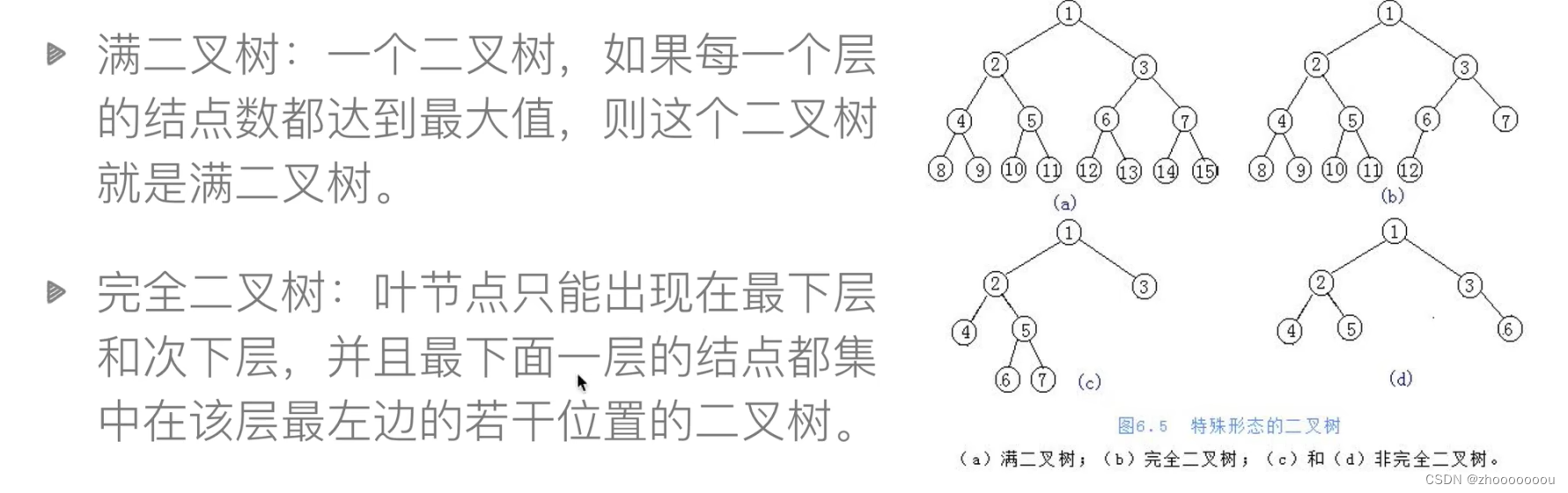
完全二叉樹：最下一層可以不滿，但節點序號必須按照從左到右排序的方式進行排列

?二叉樹的存儲方式

?因為堆排序要用到二叉樹的存儲方式，所以要了解一下

?在堆排序中我們使用順序存儲方式，那么就是把數字放到列表中，在下圖中找到父節點與左孩子和右孩子節點之間的數字關系，以方便我們去尋找數據。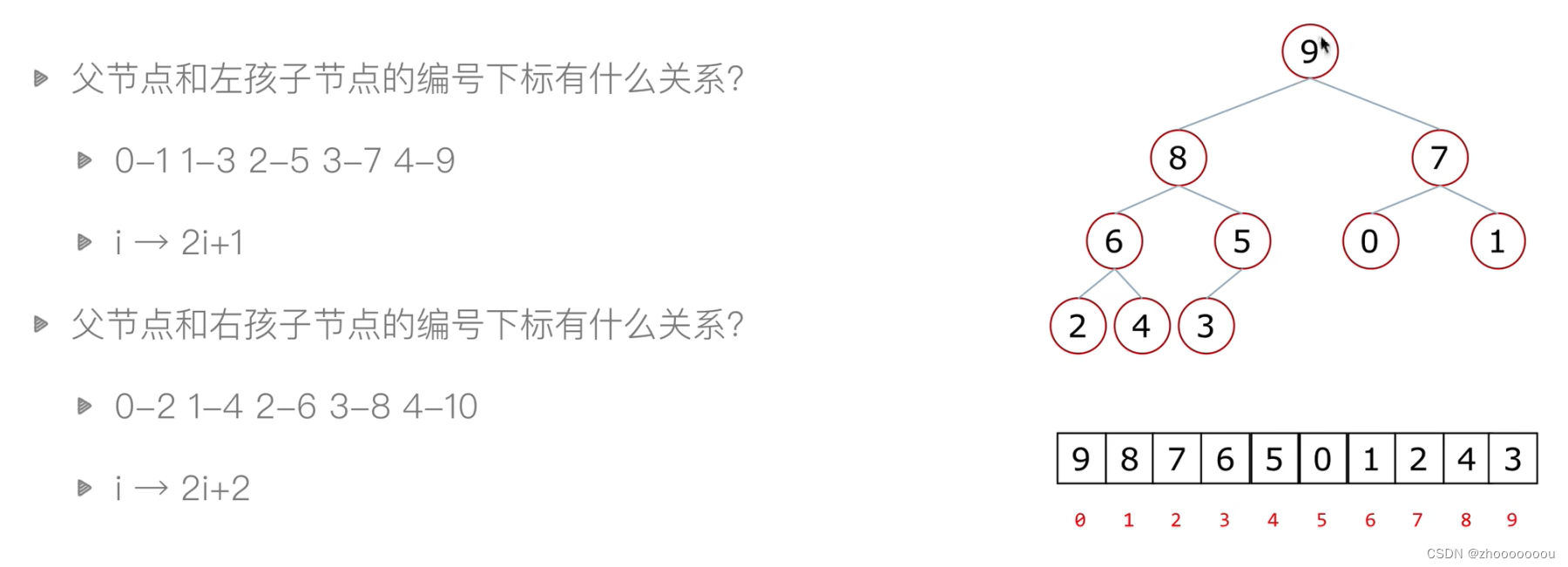

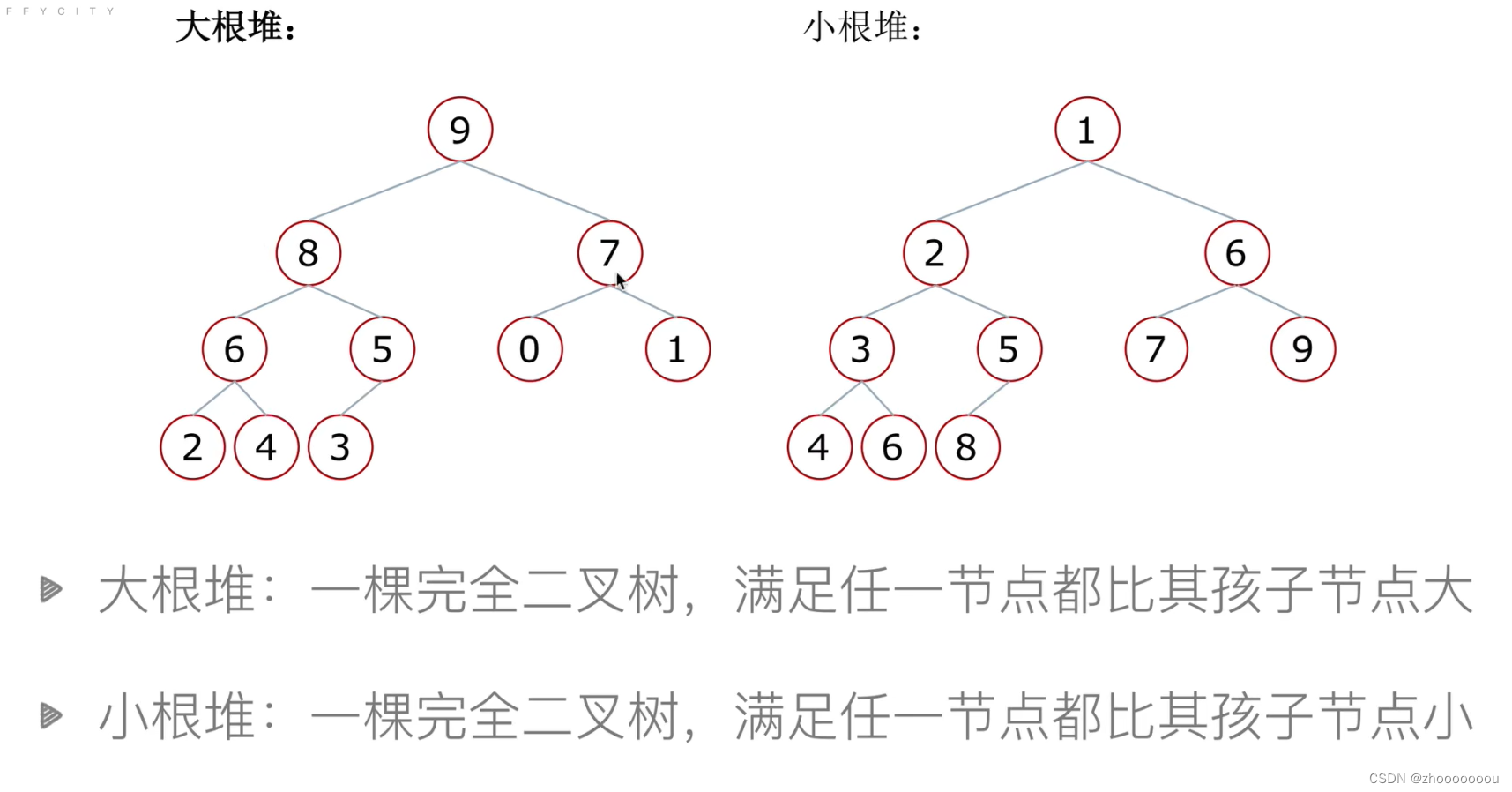
?堆排序 - 什么是堆

?

?堆的向下調整

節點的左右子樹都是堆，但自身不是堆，可以通過一次次的向下調整來將其變成一個堆。

堆排序的過程

ok代碼實現問題明日再學習。

三、學習碎碎念

慢慢開始上難度了，今天上算法課回答問題了，根據之前自己的冒泡排序的筆記，果然是一份耕耘一份收獲啊。也想對自己說別太浮躁，別太著急，慢慢來，一步一個腳印，踏踏實實的，努力的去迎接自己的未來。