2673. 使二叉樹所有路徑值相等的最小代價

題目描述：

給你一個整數?n?表示一棵?滿二叉樹?里面節點的數目，節點編號從?1?到?n?。根節點編號為?1?，樹中每個非葉子節點?i?都有兩個孩子，分別是左孩子?2 * i?和右孩子?2 * i + 1?。

樹中每個節點都有一個值，用下標從?0?開始、長度為?n?的整數數組?cost?表示，其中?cost[i]?是第?i + 1?個節點的值。每次操作，你可以將樹中?任意?節點的值?增加?1?。你可以執行操作?任意?次。

你的目標是讓根到每一個?葉子結點?的路徑值相等。請你返回?最少?需要執行增加操作多少次。

注意：

• 滿二叉樹?指的是一棵樹，它滿足樹中除了葉子節點外每個節點都恰好有 2 個子節點，且所有葉子節點距離根節點距離相同。
• 路徑值?指的是路徑上所有節點的值之和。

示例 1：

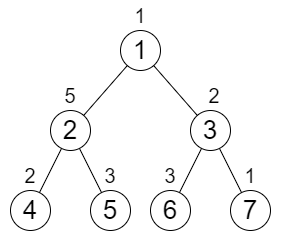
輸入：n = 7, cost = [1,5,2,2,3,3,1]
輸出：6
解釋：我們執行以下的增加操作：
- 將節點 4 的值增加一次。
- 將節點 3 的值增加三次。
- 將節點 7 的值增加兩次。
從根到葉子的每一條路徑值都為 9 。
總共增加次數為 1 + 3 + 2 = 6 。
這是最小的答案。

示例 2：

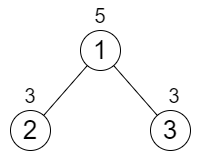
輸入：n = 3, cost = [5,3,3]
輸出：0
解釋：兩條路徑已經有相等的路徑值，所以不需要執行任何增加操作。

提示：

• 3 <= n <= 10^5
• n + 1?是?2?的冪
• cost.length == n
• 1 <= cost[i] <= 10^4

思路：

首先對于滿二叉樹來說，他可以支持隨機讀取，對于非葉子節點，2i為左孩子，2i+1為有孩子，(i)下取整為父節點。

根據題意，我們可知應該要將所有路徑上的權值和按照最大的那個路徑和來進行補齊。

（1）
考慮根到兩個互為兄弟節點（父節點相同）的葉子的兩條路徑。

由于這兩條路徑除了葉子節點不一樣，其余節點都一樣，所以為了讓這兩條路徑的路徑和相等，必須修改葉子節點的值。

設葉子節點的值分別為 x 和 y，假設 x≤y，是否需要同時增加 x 和 y 呢？

這是不需要的，把 x增加 y?x就行，因為我們可以增加它們的祖先節點的值，使得它們倆的路徑和與其它的路徑和相等，這樣可以節省操作次數。

（2）
對于不是葉子的兄弟節點，又要如何比較和計算呢？和上面的分析一樣，從根到當前節點的路徑，除了這兩個兄弟節點不一樣，其余節點都一樣。所以把路徑和從葉子往上傳，這樣就可以按照提示 1 那樣比較了。

代碼：

class Solution {public int minIncrements(int n, int[] cost) {int res=0;for(int i=n/2;i>0;i--){//從最后一個非葉子節點開始算;自底向上res+=Math.abs(cost[2*i-1]-cost[2*i]);//兩個非葉節點變成一樣的cost[i-1] += Math.max(cost[i*2-1],cost[2*i]);//累加路徑和}return res;}
}