論文解讀--Mutual Interference Mitigation in PMCW Automotive Radar

PMCW汽車雷達的相互干擾抑制

摘要

????????針對相位調制連續波(PMCW)毫米波(mmWave)汽車雷達系統中存在的相互干擾問題進行了研究。對先進駕駛輔助系統(ADAS)的需求日益增長，導致配備在同一頻段工作的毫米波雷達系統的車輛激增，導致相互干擾，可能會降低雷達性能，從而產生安全隱患。我們考慮了涉及兩個相似PMCW雷達系統的場景，并提出了一種有效的發射波形協同設計技術，使它們之間的相互干擾最小化。通過毫米波汽車雷達系統的仿真對所提出的方法進行了數值評估。結果表明，該技術顯著減少了相互干擾，提高了雷達探測性能，同時對實際汽車雷達系統的計算成本非常低，對現有基礎設施的影響微不足道。

1 介紹

?????? 毫米波(mmWave)汽車雷達系統由于其在具有挑戰性的環境中精確的目標檢測能力而獲得了極大的關注。與相機和激光雷達相比，毫米波雷達系統在大雨、霧、雪和煙霧中表現出色[1]，[2]。這些系統在77 GHz到81 GHz的頻率范圍內工作，利用高頻連續波(CW)進行目標檢測。然而，它們較差的角分辨率限制了精細空間細節的檢測。多輸入多輸出(MIMO)技術可以提高分辨率，但也會帶來相互干擾的挑戰。

????????當多個發射機在近距離工作時，MIMO雷達系統會產生相互干擾，導致底噪增加，檢測精度和可靠性降低。先進的信號處理技術，如數字波束形成和自適應濾波可以緩解這個問題[3]。隨著車載雷達系統數量的增加和毫米波頻段的擁塞，相互干擾問題日益突出[4]。調制技術，如調相連續波(PMCW)和正交頻分復用(OFDM)，與傳統的調頻連續波(FMCW)相比具有優勢，但它們需要更高的采樣率和復雜的收發器硬件[5]。

????????相互干擾抑制的研究主要集中在FMCW雷達系統的波形設計上[6]-[10]。已經提出了用于慢時間或快時間信號的自適應波形，包括慢時間編碼波形、快速生成的自適應慢時間編碼方案和快時間編碼方案[11]。偽正交噪聲波形和專門的慢時波形，如黃金碼和線性調頻CAZAC碼也被探索過[8]-[10]。

????????本文主要研究了PMCW雷達間相互干擾的抑制問題。雖然研究已經解決了FMCW和PMCW雷達之間的相互干擾問題(參見[12]-[15]以及其中的參考文獻)，但在PMCW系統的波形設計方面存在研究空白，特別是當雷達系統具有相似的物理參數時。為了解決這一差距，提出了一種設計協同波形的新框架。該框架可以處理非凸目標，在實際實現中計算效率高，并且需要對收發器基礎結構進行最小的修改。

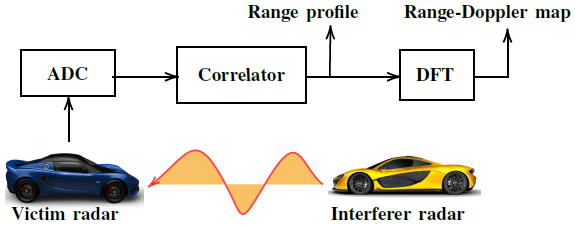
圖1:PMCW雷達工作和兩車PMCW-PMCW相互干擾的簡化示意圖。

2 問題公式化

A PMCW信號模型

?????? 在本節中，我們建立了PMCW雷達模型。我們考慮兩個PMCW汽車雷達系統，如圖1所示，它們相似且相互合作。這些雷達在同一頻帶內工作。兩個PMCW雷達在單次觸發信號中的發射信號可以描述為

?????? ? (1)

?????? 其中，fc是載波頻率，T是脈沖重復間隔（PRI），φ(t)是調制相位波形[4]。如果chirp持續時間是Tc，我們在kTc≤t≤(k +1)Tc區間內，用表示第k個chirp的相移，得到。我們假設在一個相干處理間隔(CPI)內傳輸N個信號觸發。因此，發射信號為

?????? ? (2)

?????? 其中，0≤t≤NT，同時

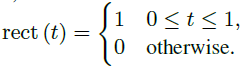?????? ? (3)

????????我們考慮一個單一目標，位于距離R處，以速度v向雷達移動，它將雷達信號反射回來。雙向目標傳播延遲為τT (t)= ，其中c為光速。接收信號為

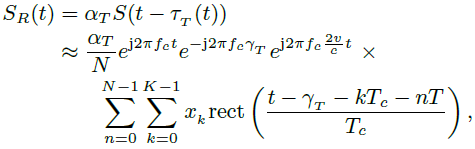??(4)

????????這里我們假設v ? c作為近似。假設兩臺雷達的協同性能消除了接收機的載波頻偏（CFO）。將接收信號SR(t)與載波頻率的共軛混合后，我們假設項和αT抵消了。我們把表示為多普勒頻率，得到

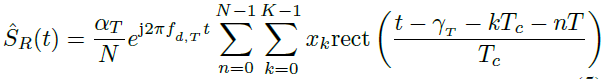??(5)

?????? 如圖1所示，在ADC中，時間分為快時間t′和慢時間索引n，時間間隔t為t = t′+ nT, t′∈[0,t]，在快時間中，信號可以間隔Tc采樣，即在t′= mTc處，得到

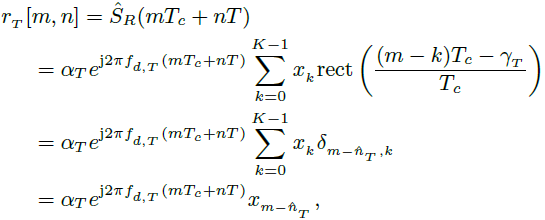?????? ? (6)

?????? 其中δi,j是克羅內克函數的擴展

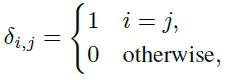?????? ? （7）

?????? 而是在距離R處由于目標引起的編碼位移。如圖1所示，在接收機中，(6)中的離散信號將通過相關器產生距離曲線。(6)與(2)的相關性為

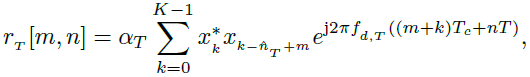?????? ? (8)

????????其為目標的距離分布[13]。第二個雷達的影響，作為一個干擾，對在受害雷達中觀察到的距離分布表示在下面的模型中。

B 相關干擾模型

?????? 受害雷達系統從干擾雷達發射機接收信號，該信號可以被接收機錯誤地解釋為來自目標的反射信號。兩臺雷達發射PMCW時的這種干擾稱為PMCW-PMCW干擾[16]。在本節中，干擾PMCW雷達系統，發射的信號相位碼為，假設與(2)類似的干擾受害雷達發射相位碼為的PMCW信號。我們將與干擾相關的單向延遲定義為，其中RI是兩個雷達系統之間的距離，vI是兩個雷達系統之間的相對速度。設為與干擾相關的多普勒頻率。受害雷達接收機的干擾采樣為

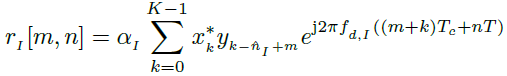?????? ? （9）

????????其中，為干擾引起的編碼位移。值得強調的是，兩臺雷達的協同性能使我們能夠有效地補償它們之間的去同步和不同的PRI。

3 相互干擾緩解

?????? 接收信號用公式表示為

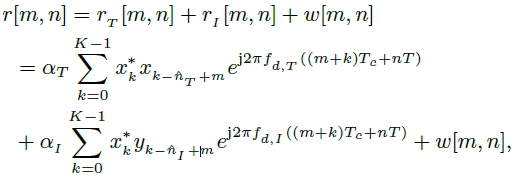??(10)

????????其中w[m, n]表示與信號無關的干擾，如接收機噪聲。在接收器中，(10)將通過對慢時間樣本應用離散傅里葉變換(DFT)進行多普勒處理器處理。因此，距離-多普勒圖是

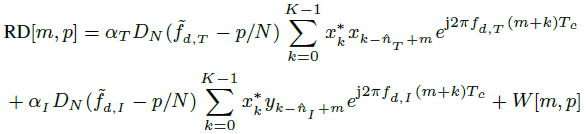?????? ? （11）

?????? 其中，是Dirichlet函數。移動的目標會改變chirp的相位。這種現象由式(11)中的項表示。因此，接收到的序列將不是純二進制序列。這種對多普勒引起的相移的敏感性被稱為多普勒不容忍[18]，在如圖2所示的距離曲線上產生了小的旁瓣。我們也很容易知道，對于PMCW雷達，距離-多普勒估計是不耦合的[13]。

?????? 如[12]所述，與快時間處理的時間尺度相比，典型的多普勒頻率非常低，即fd,I?1/Tc。從(11)中可以明顯看出，干擾是由每個距離bin中的相互關系縮放的。我們定義

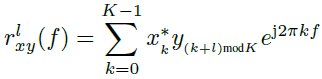??????????(12)

?????? 。由式(11)可以證明，對于，是一個優勢干擾項。為了減輕兩雷達系統之間的相互干擾，我們提出抑制干擾功率。因此，我們考慮以下關于兩個編碼x和y的優化問題:

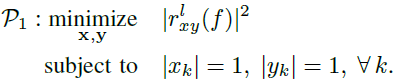??????????（13）

????????在實際場景中，車輛上的被害者雷達和干擾雷達是異步傳輸的，和都不知道。因此，我們尋求將多個網格點上的干擾最小化

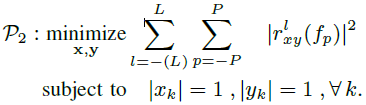?????? ? (14)

????????P的值由感興趣的最大多普勒頻率決定。引起編碼位移的干擾距離根據的關系影響許多距離bin，因此我們選擇足夠大的L以減輕所有距離bin的干擾影響。

????????備注1。(12)中的表達式可以改寫為

??????????(15)

????????其中，

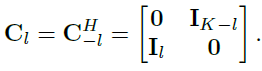??????????(16)

????????由于單模性約束，優化問題(14)是非凸的。在此，我們建議以循環的方式解決這個問題。具體來說，在我們的循環優化算法的第s次迭代中，我們首先對固定的優化x，并設置最優解為。然后，在其他條件不變的情況下，我們對固定的優化y。在下文中，我們給出了每個迭代中涉及的兩個子問題的解決方案。但首先，我們評論了非模二次規劃(UQPS)和冪方法(PMLI)迭代來解決這類問題。

????????備注2。UQP定義為

?????? ? （17）

????????其中為單模向量的集合。第s次PMLI迭代時的單模向量序列

?????? ? (18)

?????? 導致當G是正定矩陣時，UQP的目標值單調遞增。此外，在不改變最優解的情況下，采用對角加載技術保證了矩陣的正定性。特別地，在(17)中，對角線加載， λm略大于G的最大特征值，導致了一個等價問題，給我們留下了一個正定的eG[19]。

?????? ?固定y下x的優化:將(15)代入(14)，相關問題變為

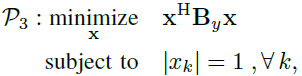?????? ? （19）

?????? 其中。通過備注2介紹的對角加載技術，我們得到了正定矩陣，得到了等效問題

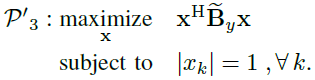?????? ? （20）

?????? ?固定x下 y的優化:關于y的問題，稍作修改，是

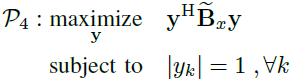?????? ? (21)

?????? 。

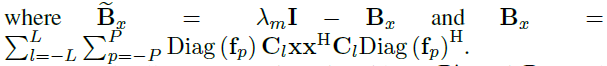?????? 我們循環優化子問題P'3和P4，直到收斂。每個子問題都通過在備注2中介紹的PMLI迭代來解決。算法1總結了該算法的步驟。(14)在迭代s時的目標值用表示。在下文中，我們對所提出的算法進行了數值評估。

算法1 PMCW波形的相互干擾抑制設計

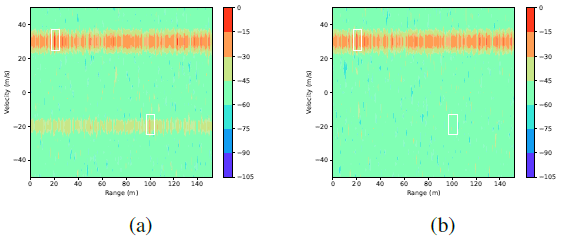
圖2:a)隨機PMCW信號和b)算法1生成的PMCW波形的單個目標距離-多普勒圖。

4 數值評估

????????我們考慮了兩輛裝有雷達的車輛，雷達發射PMCW波形，工作頻率為fc = 79 GHz，脈沖持續時間為T = 6.66 ns。發射N = 140個觸發信號，在接收信號中加入分布為的高斯白噪聲，假設目標和干擾RCS為35 dBsm。目標放置在距離R = 20 m處，以速度v = 30 m/s移動。假設干擾雷達位于距離RI = 200 m處，相對速度vI =?20 m/s。如圖2 (a)和(b)所示，分別采用算法1隨機生成K = 50個chirp的PMCW波形，目標場景的二維距離多普勒圖像。可以看到，在圖2(a)中，干擾的功率很強，導致虛警。優化后的PMCW波形可以有效地抑制干擾，從而提高雷達的目標探測性能。