智能駕駛規劃控制理論學習02-基于搜索的路徑規劃方法

一、路徑搜索問題

二、圖論基礎

三、圖搜索方法

1、廣度優先搜索（BFS）

bfs與dfs的區別

bfs的搜索過程????????

bfs的算法實現

2、迪杰斯特拉算法（Dijkstra）

核心思想

優先級隊列

Dijkstra搜索過程

Dijkstra優缺點分析

3、A*算法

核心思想

A*搜索過程????????

啟發式函數

總結

動態規劃

一、路徑搜索問題

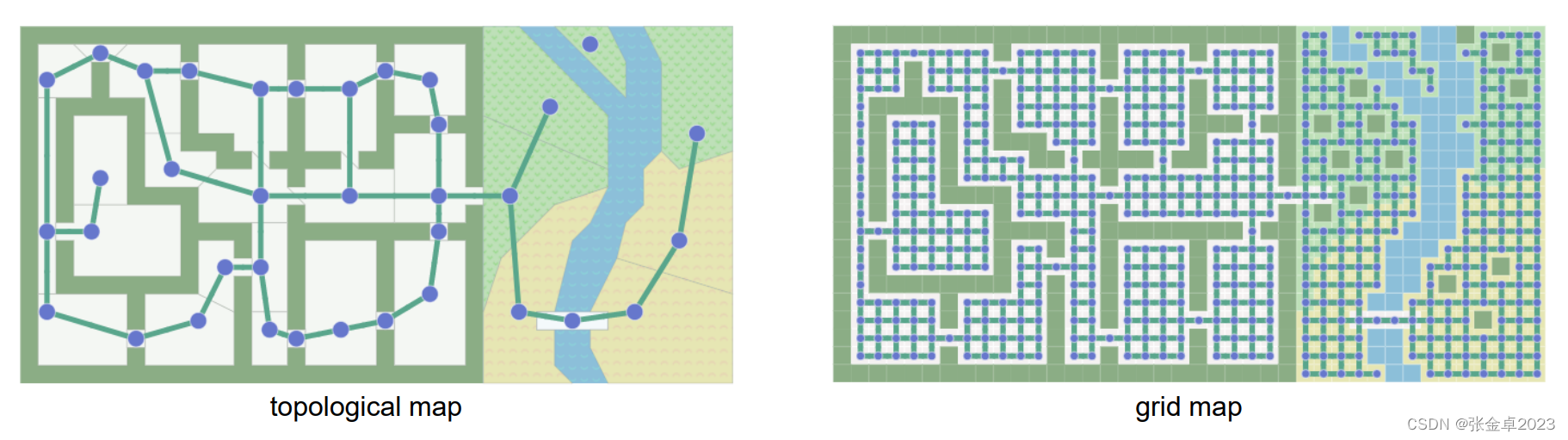
? ? ? ? 當我們要搜索一個從起到到終點的最優路徑時，要思考何為最優？是從距離角度、時間角度還是其他方面。為了找到一條這樣的路徑，我們通常會使用一種圖像搜索算法，這樣地圖就可以作為一個圖表進行使用。

? ? ? ? 對于這種路徑搜索問題，將圖表上的一系列位置作為節點、它們之間的連線以及起點終點（拓撲地圖信息）作為輸入，得到的輸出是由節點和邊構成的網格地圖。

二、圖論基礎

? ? ? ? 在圖論中可以將圖簡單分為無向圖(Undirected Graph)、有向圖(Directed Graph)和權重圖(Weighted Graph)。

?????????在圖論中，圖由頂點（vertices）和邊（edges）組成。頂點代表圖中的個體或實體，而邊表示頂點之間的關系或連接。這種連接可以是有向的或無向的，具體取決于圖的類型和定義。

????????在圖論中，圖的權（Weight）指的是在圖的邊上賦予的一個數值或度量，用于表示頂點之間的關系或連接的強度、距離、成本等信息。

三、圖搜索方法

? ? ? ? 本節主要介紹圖搜索中常用的算法：廣度優先算法（BFS）、迪杰斯特拉算法和A*算法。

1、廣度優先搜索（BFS）

bfs與dfs的區別

bfs是先把本節點所連接的所有節點遍歷一遍，走到下一個節點的時候，再把連接節點的所有節點遍歷一遍，搜索方向更像是四面八方的搜索過程。
深度優先搜索是向一個方向去搜，不到黃河不回頭，直到遇到絕境了，搜不下去了，再換方向（換方向的過程就涉及到了回溯）。

? ? ? ? 相比較而言，廣搜的搜索方式就適合于解決兩個點之間的最短路徑問題。

bfs的搜索過程????????

? ? ? ? 這里利用隊列的方式對bfs算法的搜索過程進行介紹，一開始先將起始節點入隊，利用隊列先進先出的特點在起始節點出隊時將與起始節點相連的其他節點以此入隊，然后繼續重復上述的過程，再將隊首元素彈出，將與之相鄰的未訪問過的節點依次添加入隊，循環直到遇到目標節點或隊列為空。

bfs的算法實現

? ? ? ? 在代碼隨想錄（新更新篇）中有介紹過bfs蘇娜發的C++實現，這里就直接引用了。

int dir[4][2] = {0, 1, 1, 0, -1, 0, 0, -1}; // 表示四個方向
// grid 是地圖，也就是一個二維數組
// visited標記訪問過的節點，不要重復訪問
// x,y 表示開始搜索節點的下標
void bfs(vector<vector<char>>& grid, vector<vector<bool>>& visited, int x, int y) {queue<pair<int, int>> que; // 定義隊列que.push({x, y}); // 起始節點加入隊列visited[x][y] = true; // 只要加入隊列，立刻標記為訪問過的節點while(!que.empty()) { // 開始遍歷隊列里的元素pair<int ,int> cur = que.front(); que.pop(); // 從隊列取元素int curx = cur.first;int cury = cur.second; // 當前節點坐標for (int i = 0; i < 4; i++) { // 開始想當前節點的四個方向左右上下去遍歷int nextx = curx + dir[i][0];int nexty = cury + dir[i][1]; // 獲取周邊四個方向的坐標if (nextx < 0 || nextx >= grid.size() || nexty < 0 || nexty >= grid[0].size()) continue;  // 坐標越界了，直接跳過if (!visited[nextx][nexty]) { // 如果節點沒被訪問過que.push({nextx, nexty});  // 隊列添加該節點為下一輪要遍歷的節點visited[nextx][nexty] = true; // 只要加入隊列立刻標記，避免重復訪問}}}}

? ? ? ? bfs向各個方向搜索的可能性都相同，如果各邊的權重都為1，那么使用BFS算法進行搜索就是最優的。但是在大多數情況下，往往各個方向的運動都會有不同的代價值（權重），如何對這些具有不同權重的圖進行處理就就要引出下面的算法了。

2、迪杰斯特拉算法（Dijkstra）

核心思想

? ? ? ? 與BFS直接將隊列中彈出元素相連的所有元素都存入隊列，Dijkstra利用貪心的思想每次選擇都是累計代價值最小的節點進行相加。

? ? ? ? 具體來說，Dijkstra創建了一個先變量g(n)，以此來代替從起始節點到達當前節點所消耗的代價值，每次從開放集openset中尋找累計大價值最小的節點進行相加，而不是訪問隊列中的第一個元素。

優先級隊列

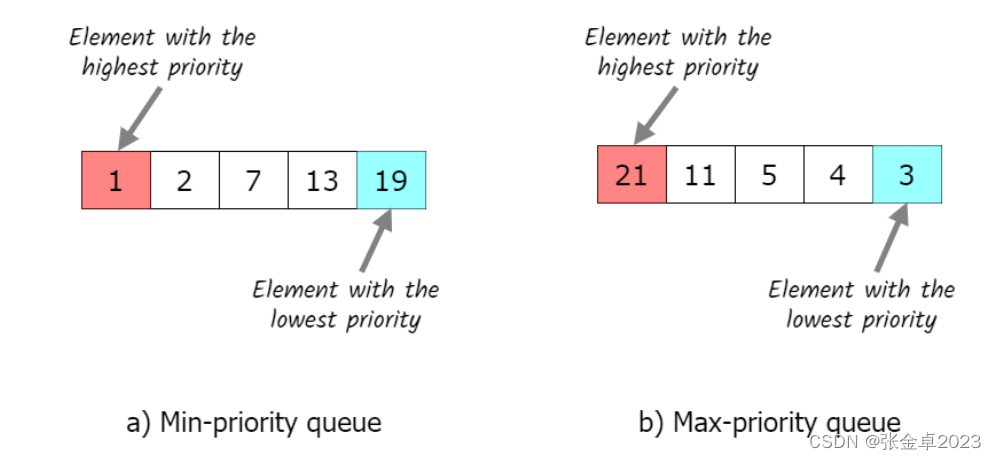
? ? ? ? 優先級隊列中每一個元素都有著與之對應的優先級。在優先級隊列中，優先級高的元素會比優先級低的元素先訪問。

Dijkstra搜索過程

? ? ? ? 輸入：一個圖表（包含節點和路徑的集合）和一個起始節點；

? ? ? ? 輸出：到任意節點的最短路徑。

? ? ? ? 用偽代碼進行簡潔描述：????????

Algorithm Dijkstra(G, start):let open_list be pirority queueopen_list.push(start, 0)g[start] := 0while (open_list is not empty):current := open_list.pop()mark current as visitedif current is the goal:return currentfor all unvisited neighbours next of current in Graph G:next_code := g[current] + cost(current, next)if next is not in open_list:open_list.push(next, next_cost)else:if g[next] > next_cost:g[next] := next_cost

? ? ? ? 先創建一個優先級隊列open_list，將起始節點存入優先級隊列，并設置累計代價函數的初值為0，然后進行循環（循環終止條件設為優先級隊列非空），在循環中每次彈出優先級隊列中的節點就要判斷是否是目標節點，如果是目標節點就直接返回，若不是就要將彈出節點設為已訪問節點，并對圖表中當前彈出節點周圍的其余鄰居節點進行判斷，若是未訪問節點則直接存入優先級隊列，若已訪問則進行累計代價函數更新。

Dijkstra優缺點分析

? ? ? ? 優點：

Dijkstra算法可以尋找到起始節點到圖表上其他所有節點的最短路徑；
Dijkstra孫發滿足最優原則。

? ? ? ? 缺點：

該算法始終在優先級隊列中尋找最短路徑，而不考慮方向或距離目標的遠近。因此，若使用它來搜索一個特定目標的最短路徑時，并不高效。

3、A*算法

核心思想

? ? ? ? A*算法在Dijkstra算法的基礎上引入啟發式函數作為對目標節點的引導，從而提高了搜索的效率。

????????啟發式函數h(n)表示從節點n到目標的估計代價。使用f-score來評估每個節點的代價：f(n) = g(n) + h(n)，然后在優先級隊列中選取f-score最小的節點，而不是Dijkstra中的g-score。

A*搜索過程????????

Algorithm Astar(G, start):let open_list be priority queueg[start] := 0f[start] = g[start] + h[start]open_list.push(start, f[start])while (open_list is not empty):current := open_list.pop()mark current as visitedif current is the goal:return currentfor all unvisited neighbours next of current in Graph G:next_cost := g[current] + cost(current, next)if next is not in open_list:open_list.push(next, next_cost + h[next]else:if g[next] > next_costg[next] = next_costf[next] = next_cost + h[next]

? ? ? ? 依然是創建一個優先級隊列，并對g(n)和f(n)賦初值（假設啟發式函數h(n)）已知，再將初始節點和其對應的f-socre存入優先級隊列，然后開始進入循環（循環的終止條件式隊列非空），彈出隊列中的節點，將其標志為已訪問，若該節點為目標節點直接返回，否則要對其在圖表中的鄰居節點進行判斷，若鄰居節點未被訪問則存入優先級隊列中，存放時對應的代價函數還要加上h-score，若已訪問則進行代價值更新。

啟發式函數

? ? ? ? A*算法有別于Dijkstra的最大之處就在于啟發算法的加入，但是在路徑搜索問題中沒有特定的啟發式函數，因為每一種情況都是不同的。

? ? ? ? 要注意啟發式函數不能過高的估計代價值，只要啟發式函數提供的估計值小于真實值，那么A*總會找到一條最優的路徑并且通常比Dijkstra效率高。

? ? ? ? 如果啟發式函數的代價值估計過高了，會產生什么影響呢，以下圖為例：

? ? ? ? ?圖中所示的B節點對應的啟發式函數估計的代價值高于其真實值，因此C節點的f-score高于B節點的f-score，因此會錯誤地優先選擇C節點通過，但實際上B節點才是更優的選擇。

? ? ? ? A*搜索的效率與精度也取決于啟發式函數的選擇，主要有以下四種情況：

h(n) = 0：此時f-socre = g-score A*算法退化為Dijkstra算法；
h(n) < cost(n, goal)：A*滿足最優性，搜索效率上高于Dijkstra算法；
h(n) = cost(n, goal)：A*滿足最優性，并且達到最高搜索效率；
h(n) > cost(n, goal)：啟發式函數高估了實際代價，不具有最優性。

總結

BFS在各個方向上的搜索可能性相同，并且如果各邊權重為1，bfs搜索得到的路徑滿足最優性；
Dijkstra算法利用貪心的思想選擇累計代價值最低的節點，并且能夠在有權圖中表現出最優性，如果各邊權重為1，那么Dijkstra搜索得到的路徑和BFS搜索得到的相同。
A*是Dijkstra的改進，通過加入啟發式函數提高搜索的效率，啟發式函數的設計會直接影響到搜索的效率和精度。