目錄

引入：

例題1：按摩師（打家劫舍I）

例題2：打家劫舍II

例題3：刪除并獲得點數

例題4：粉刷房子

例題5：買賣股票的最佳時機含冷凍

結語：

---

引入：

相信看到這里的友友們對動態規劃已經有了一定的了解，下面我將介紹動態規劃的簡單多狀態dp問題。所謂多狀態就是在一步下有不同的情況要區分（例如買股票，今天可以分為買還是不買的多兩種情況）。由于算法只講知識點是遠遠不夠的故下面我會在例題中穿插知識點幫助理解。動態規劃一般的解題步驟還是1. 狀態表示，2.狀態轉移方程，3.初始化，4.填表順序，5.返回值。在寫代碼時一定要把這5步考慮清楚再寫代碼。

例題1：按摩師（打家劫舍I）

鏈接：按摩師

題目簡介：

一個有名的按摩師會收到源源不斷的預約請求，每個預約都可以選擇接或不接。在每次預約服務之間要有休息時間，因此她不能接受相鄰的預約。給定一個預約請求序列，替按摩師找到最優的預約集合（總預約時間最長），返回總的分鐘數。

解法（動態規劃）：

1. 狀態表示：

對于簡單的線性dp ，我們可以用「經驗+題?要求」來定義狀態表示例如：

（1）以某個位置為結尾的最小花費。

（2）以某個位置為起點到終點的最小花費。

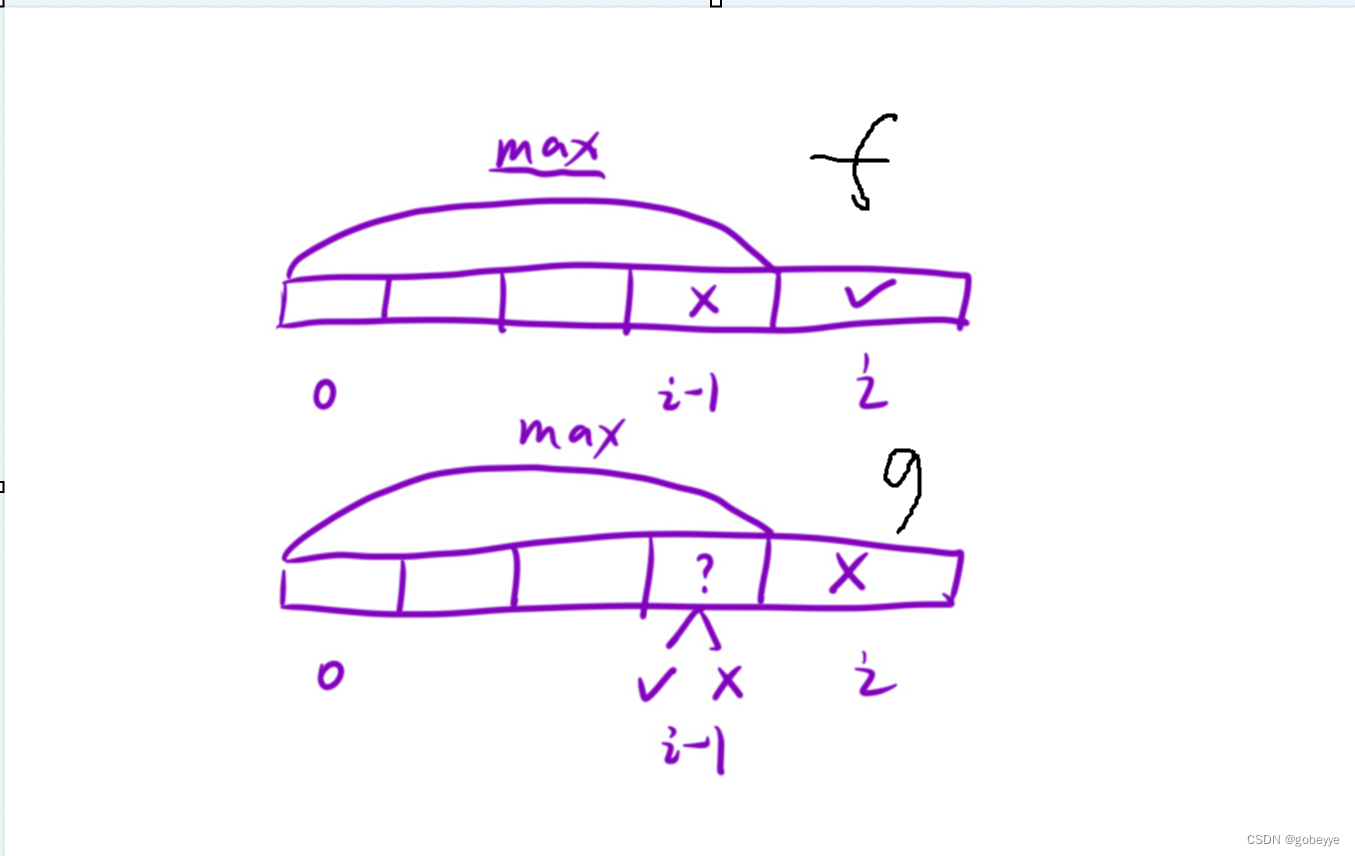
故我們這題采用常用的方式：dp[i] 表?：選擇到i 位置時，此時的最?預約時?。由于我們這個題在i 位置的時候，會?臨選擇或者不選擇兩種抉擇，所依賴的狀態需要細分。

下面之所以用f和g是因為高中我們所學的f（x）和g（x），可以換成其他的（但最好用f和g就當作是不成文的規定，這樣代碼的可讀性會更高）。

（1）f[i] 表示：選擇到i 位置時， nums[i] 必選，此時的最?預約時?。

（2）g[i]表示：選擇到i 位置時， nums[i] 不選，此時的最?預約時?。

2.狀態轉移方程

因為狀態表示定義了兩個，因此我們的狀態轉移?程也要分析兩個：

對于f[i] ：

如果nums[i] 必選，那么我們僅需知道i - 1 位置在不選的情況下的最?預約時?， 然后加上nums[i] 即可，因此f[i] = g[i - 1] + nums[i] 。

對于g[i] ：

如果nums[i] 不選，那么i - 1 位置上選或者不選都可以。因此，我們需要知道i - 1 位置上選或者不選兩種情況下的最?時?，因此g[i] = max(f[i - 1], g[i - 1]) 。

在狀態轉移方程這里可以畫圖來幫助我們理解

3.初始化

這道題的初始化?較簡單，因此?需加輔助節點（前兩篇文章已解釋），僅需初始化f[0] = nums[0], g[0] = 0 即可。

4.填表順序

根據「狀態轉移?程」得「從左往右，兩個表?起填」。

5.返回值

根據「狀態表示」，應該返回max(f[n - 1], g[n - 1]) 。

代碼實現如下：

class Solution {public int massage(int[] nums) {//1.創建dp表//2.初始化//3.填表//4.返回值int n = nums.length;if(n == 0){return 0;}int[] f = new int[n];//選擇int[] g = new int[n];//不選擇f[0] = nums[0];for(int i = 1;i < n;i++){f[i] = g[i - 1] + nums[i];g[i] = Math.max(g[i - 1],f[i - 1]);}return Math.max(g[n -1],f[n - 1]);}
}

時間復雜度：O（n）

空間復雜度：O（n）

例題2：打家劫舍II

鏈接：打家劫舍II

題目簡介：

你是一個專業的小偷，計劃偷竊沿街的房屋，每間房內都藏有一定的現金。這個地方所有的房屋都?圍成一圈?，這意味著第一個房屋和最后一個房屋是緊挨著的。同時，相鄰的房屋裝有相互連通的防盜系統，如果兩間相鄰的房屋在同一晚上被小偷闖入，系統會自動報警?。

給定一個代表每個房屋存放金額的非負整數數組，計算你?在不觸動警報裝置的情況下?，今晚能夠偷竊到的最高金額。

?解法（動態規劃）：

通過閱讀題目友友可以發現這題和例題一是差不多的，唯一不同就是例題二加了一個末尾和開頭的限制。上?個問題是?個「單排」的模式，這?個問題是?個「環形」的模式，也就是?尾是相連的。但是我們可以將「環形」問題轉化為「兩個單排」問題：

（1）偷第?個房屋時的最大?額x ，此時不能偷最后?個房?，因此就是偷[0, n - 2] 區間的房?。

（2）不偷第?個房屋時的最大?額y ，此時可以偷最后?個房?，因此就是偷[1, n - 1] 區 間的房?。

兩種情況下的「最大值」，就是最終的結果。

代碼如下：

下面的rob1方法就是例題一。

class Solution {public int rob(int[] nums) {int n = nums.length;return Math.max(nums[0] + rob1(nums,2,n - 2), rob1(nums,1,n - 1));}public int rob1(int[] nums,int left,int right){if(left > right){return 0;}//1.創建dp表//2.初始化//3.填表//4.返回值int n = nums.length;int[] f = new int[n];int[] g = new int[n];f[left] = nums[left];for(int i = left + 1;i <= right;i++){f[i] = g[i - 1] + nums[i];g[i] = Math.max(g[i - 1],f[i - 1]);}return Math.max(f[right],g[right]);}
}

時間復雜度：O（n）?

空間復雜度：O（n）

例題3：刪除并獲得點數

鏈接：刪除并獲得點數

題目簡介：

給你一個整數數組?nums?，你可以對它進行一些操作。

每次操作中，選擇任意一個?nums[i]?，刪除它并獲得?nums[i]?的點數。之后，你必須刪除?所有?等于?nums[i] - 1?和?nums[i] + 1?的元素。

開始你擁有?0?個點數。返回你能通過這些操作獲得的最大點數。

解法（動態規劃）：

其實這道題依舊是「打家劫舍I」問題的變型。?我們注意到題?描述，選擇x 數字的時候， x - 1 與x + 1 是不能被選擇的。像不像「打家劫舍」問題中，選擇i 位置的?額之后，就不能選擇i - 1 位置(數組中)以及i + 1 位置的?額呢~?因此，我們可以創建?個??為10001 （根據題?的數據范圍）的hash 數組，將nums 數 組中每?個元素x ，累加到hash 數組下標為x 的位置處，然后在hash數組上來?次「打家劫舍」即可。

過程如下圖：

弧線表示0到i - 1之間能獲得的最大點數。

代碼如下：

class Solution {public int deleteAndEarn(int[] nums) {//1.創建dp表//2.初始化//3.填表//4.返回值int n = 10001;int[] arr = new int[n];for(int x:nums){arr[x] += x;}int[] f = new int[n];int[] g = new int[n];f[0] = arr[0];for(int i = 1;i < n;i++){f[i] = g[i - 1] + arr[i];g[i] = Math.max(f[i - 1],g[i - 1]);}return Math.max(f[n - 1],g[n - 1]);}
}

時間復雜度：O（n）?

空間復雜度：O（n）

例題4：粉刷房子

鏈接：粉刷房?

題目簡介：

?解法（動態規劃）：

?1. 狀態表示：

對于線性dp ，我們可以?「經驗+題?要求」來定義狀態表?：但是我們這個題在i 位置的時候，會?臨「紅」「藍」「綠」三種抉擇，所依賴的狀態需要細分：

（1）dp[i][0] 表?：粉刷到i 位置的時候，最后?個位置粉刷上「紅?」，此時的最?花費。?

（2）dp[i][1] 表?：粉刷到i 位置的時候，最后?個位置粉刷上「藍?」，此時的最?花費。

（3）dp[i][2] 表?：粉刷到i 位置的時候，最后?個位置粉刷上「綠?」，此時的最?花費。

?2.狀態轉移方程

因為狀態表?定義了三個，因此我們的狀態轉移?程也要分析三個：

對于dp[i][0] ：

如果第i個位置粉刷上「紅?」，那么i-1位置上可以是「藍?」或者「綠?」。因此我們 需要知道粉刷到i-1位置上的時候，粉刷上「藍?」或者「綠?」的最?花費，然后加上i?位置的花費即可。于是狀態轉移?程為： dp[i][0] = min(dp[i - 1][1], dp[i - 1][2]) + costs[i - 1][0] ;

同理，我們可以推導出另外兩個狀態轉移?程為：

dp[i][1] = min(dp[i - 1][0], dp[i - 1][2]) + costs[i - 1][1] ；

dp[i][2] = min(dp[i - 1][0], dp[i - 1][1]) + costs[i - 1][2] 。

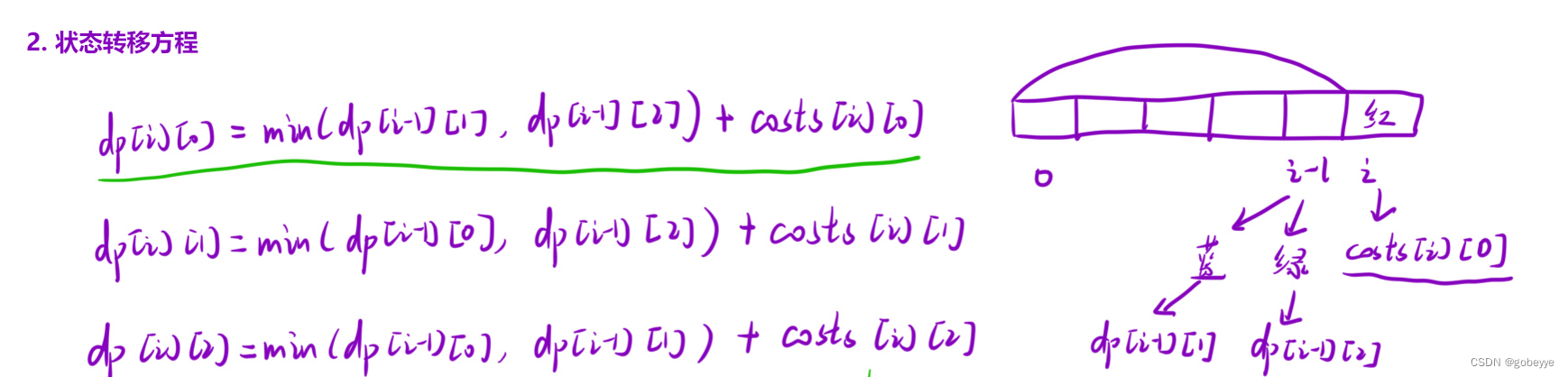
?3.初始化

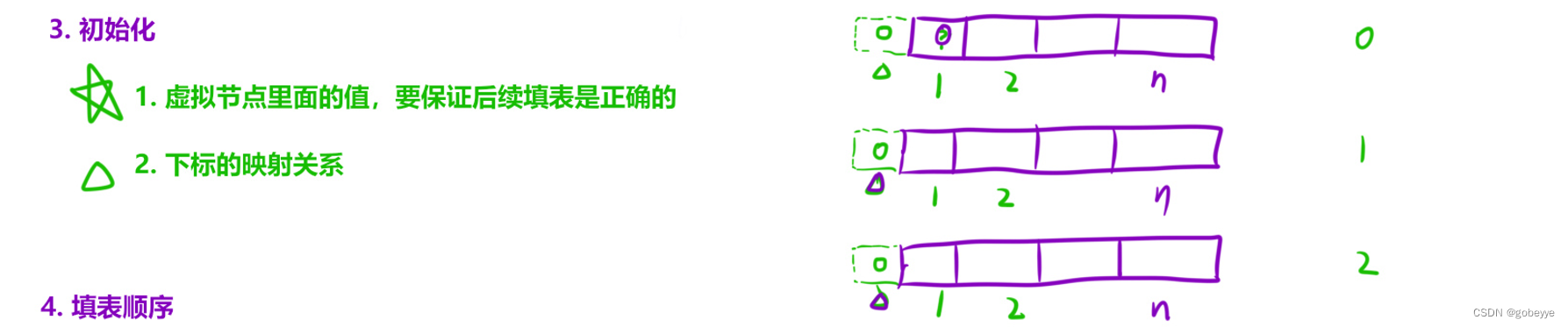
采用最前?加上?個「輔助結點」。

注意點：(1)輔助結點??的值要「保證后續填表是正確的」(2)「下標的映射關系」。

?4.填表順序

?5.返回值

根據「狀態表?」，應該返回最后?個位置粉刷上三種顏?情況下的最?值，因此需要返回： min(dp[n][0], min(dp[n][1], dp[n][2])) 。

代碼如下：

class Solution {public int minCost(int[][] costs) {//1.創建dp表//2.初始化//3.填表//4.返回值int n = costs.length;int[][] dp = new int[n + 1][3];for(int i = 1;i <= n;i++){dp[i][0] = Math.min(dp[i - 1][1],dp[i - 1][2]) + costs[i - 1][0];dp[i][1] = Math.min(dp[i - 1][0],dp[i - 1][2]) + costs[i - 1][1];dp[i][2] = Math.min(dp[i - 1][1],dp[i - 1][0]) + costs[i - 1][2];}return Math.min(dp[n][0],Math.min(dp[n][1],dp[n][2]));}
}

時間復雜度：O（n）?

空間復雜度：O（n）

例題5：買賣股票的最佳時機含冷凍

鏈接：買賣股票的最佳時機含冷凍期

題目簡介：

??解法（動態規劃）：

?1. 狀態表示：

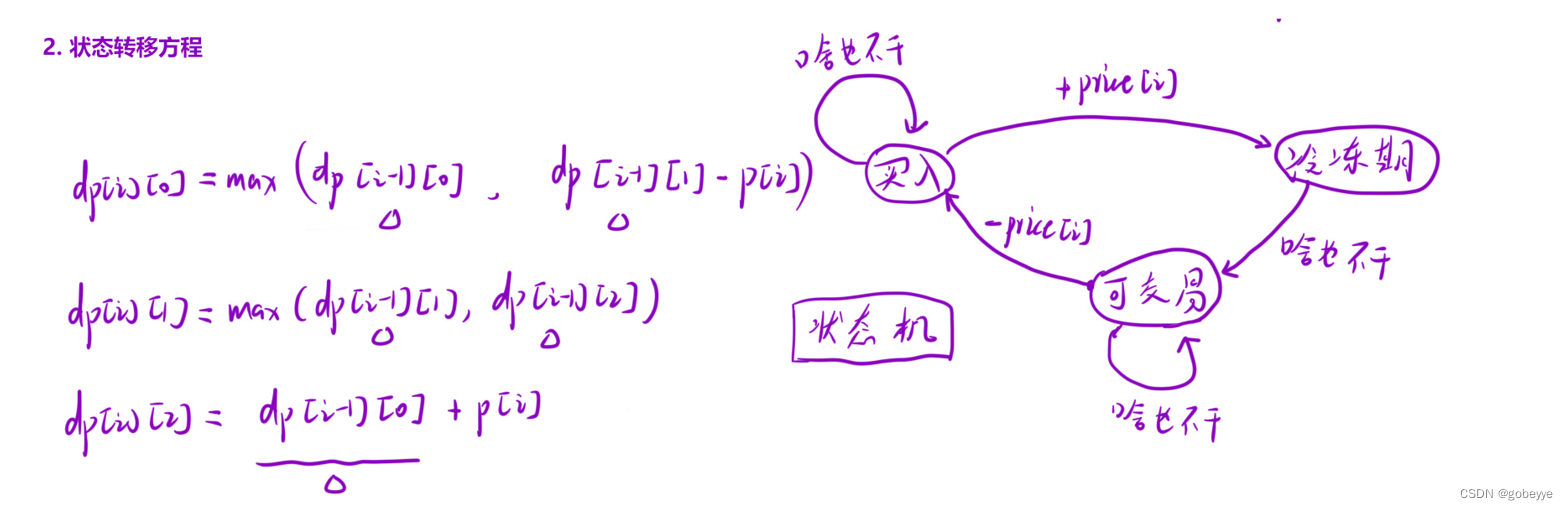
這?我們選擇?較常?的?式，以某個位置為結尾，結合題?要求，定義?個狀態表?：由于有「買?」「可交易」「冷凍期」三個狀態，因此我們可以選擇?三個數組，其中：

（1）dp[i][0] 表?：第i 天結束后，處于「買?」狀態，此時的最?利潤。

（2）dp[i][1] 表?：第i 天結束后，處于「可交易」狀態，此時的最?利潤。

（3）dp[i][2] 表?：第i 天結束后，處于「冷凍期」狀態，此時的最?利潤。

我們要謹記規則：

（1）處于「買?」狀態的時候，我們現在有股票，此時不能買股票，只能繼續持有股票，或者賣 出股票；

（2）處于「買?」狀態的時候，我們現在有股票，此時不能買股票，只能繼續持有股票，或者賣 出股票；

?2.狀態轉移方程

確定狀態表示后，我們可以畫圖來幫助我們理解根據題目要求我們可以畫圖下圖，并推出狀態轉移方程。

?3.初始化

三種狀態都會?到前?個位置的值，因此需要初始化每??的第?個位置：

dp[0][0] ：此時要想處于「買?」狀態，必須把第?天的股票買了，因此dp[0][0] = - prices[0] ； dp[0][1] ：啥也不??即可，因此dp[0][1] = 0 ；

dp[0][2] ：手上沒有股票，買?下賣?下就處于冷凍期，此時收益為0 ，因此 dp[0][2] = 0 。

4.填表順序

根據「狀態表?」，我們要三個表?起填，每?個表「從左往右」。

5.返回值

應該返回「賣出狀態」下的最?值，因此應該返回max(dp[n - 1][1], dp[n - 1] [2]) 。

代碼如下：

class Solution {public int maxProfit(int[] prices) {//1.創建dp表//2.初始化//3.填表//4.返回值int n = prices.length;int[][] dp = new int[n][3];dp[0][0] = -prices[0];for(int i = 1;i < n;i++){dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] - prices[i]);dp[i][1] = Math.max(dp[i - 1][1],dp[i - 1][2]);dp[i][2] = dp[i - 1][0] + prices[i];}return Math.max(dp[n - 1][1],dp[n - 1][2]);}
}

時間復雜度：O（n）?

空間復雜度：O（n）

結語：

其實寫博客不僅僅是為了教大家，同時這也有利于我鞏固自己的知識點，和一個學習的總結，由于作者水平有限，對文章有任何問題的還請指出，接受大家的批評，讓我改進，如果大家有所收獲的話還請不要吝嗇你們的點贊收藏和關注，這可以激勵我寫出更加優秀的文章。