• 順序（線性）查找
• 二分查找/折半查找
• 插值查找
• 斐波那契查找

線性查找

判斷數列是否包含要求，如果找到了，就提示找到了，并給出下標值

// 線性查找
public static ArrayList<Integer> seqSearch(int[] arr, int value) {ArrayList<Integer> list = new ArrayList<>();for (int i = 0; i < arr.length; i++) {if (value == arr[i]) {list.add(i);}}return list;
}

---

二分查找

需要對一個有序數組進行二分查找 {1, 8, 10, 89, 1000, 1234}，輸入一個數
看看該數組是否存在此數，并且求出下標，如果沒有就提示”沒有這個數”。

思路

1. 確定該數組的中間的下標

   可以向下取整，也可以向上取整。e.g:4.5向上取整為 5;向下去整為4，此處演示為向下取整
   

   mid=(left+right)/2

2. 讓需要查找的數findVal和arr[mid]比較

   • findVal>arr[mid，說明你要查找的數在mid的右邊，因此需要遞歸的向右查找
   • findVal<arr[mid]，說明你要查找的數在mid的左邊，因此需要遞歸的向左查找
   • findVal==arr[mid說明找到，就返回

3. 遞歸結束

   • 找到就結束遞歸
   • 遞歸完整個數組，仍然沒有找到findVal,也需要結束遞歸當Ieft>right就需要退出

/**
* 二分查找 ---要求數組為有序數組
* @param arr 需要查詢的數組
* @param left 數組的最左側下標
* @param right 數組的最右側下標
* @param findVal 需要查詢的值
* @return
*/
public static int binarySearch(int[] arr, int left, int right, int findVal) {// 當 left > right 時，整個數組遍歷后并未找到值if (left > right) {return -1;}int mid = (left + right) / 2;int midVal = arr[mid];if (findVal > midVal) {// 右遞歸return binarySearch(arr, mid + 1, right, findVal);} else if (findVal < midVal) { // 向左遞歸return binarySearch(arr, left, mid - 1, findVal);} else {return mid;}
}

二分優化—多索引返回

// 二分查找 ---要求數組為有序數組
public static ArrayList<Integer> binarySearch(int[] arr, int left, int right, int findVal) {// 當 left > right 時，整個數組遍歷后并未找到值if (left > right) {return new ArrayList<Integer>();}int mid = (left + right) / 2;int midVal = arr[mid];if (findVal > midVal) {// 右遞歸return binarySearch(arr, mid + 1, right, findVal);} else if (findVal < midVal) { // 向左遞歸return binarySearch(arr, left, mid - 1, findVal);} else {// 找到值ArrayList<Integer> resIndexList = new ArrayList<>();// 向 mid 的左右兩邊掃描
//            int temp = mid - 1;
//            while (true) {// 向左
//                if (temp < 0 || arr[temp] != findVal) {// 退出
//                    break;
//                }
//                // 否則，就temp 放入到resIndexList
//                resIndexList.add(temp);
//                temp -= 1; // temp左移
//            }
//            resIndexList.add(mid); // 將中間索引加入
//
//            temp = mid + 1;
//            while (true) {// 向右
//                if (temp > arr.length - 1 || arr[temp] != findVal) {// 退出
//                    break;
//                }
//                // 否則，就temp 放入到resIndexList
//                resIndexList.add(temp);
//                temp += 1; // temp右移
//            }// 再優化resIndexList.add(mid); // 將中間索引加入for (int i = mid - 1; i >= 0; i--) {// 向左if (arr[i] != findVal) {break;}resIndexList.add(i);}for (int i = mid + 1; i <= arr.length - 1; i++) {// 向右if (arr[i] != findVal) {break;}resIndexList.add(i);}return resIndexList;}
}

---

插值查找

需要數組是有序，效率比二分查找更高效

• 插值查找算法類似于二分查找，不同的是插值查找每次從自適應mid處開始查找。

• 將折半查找中的求mid索引的公式，low表示左邊索引，high表示右邊索引right

• $mid=\frac{low+high}{2}=low+\frac{1}{2}(high?low)$ ?? $mid=low+\frac{key?a[low]}{a[high]?a[low]}(high?low)$ 【其中key為需要查找的值】

• 公式優化：int $midIndex=low+(high?low)?(key?arr[low])/(arr[high]?arr[low]);$

// 插值查找 ---要求數組為有序數組
// 其中key為需要查找的值
public static int insertValueSearch(int[] arr, int left, int right, int key) {// 注意：key < arr[0] || key > arr[arr.length - 1]必須要有（優化作用），否則可能會造成midIndex越界if (left > right || key < arr[0] || key > arr[arr.length - 1]) {return -1;}int midIndex = left + (right - left) * (key - arr[left]) / (arr[right] - arr[left]);int midVal = arr[midIndex];if (key > midVal) {// 向右掃描遞歸return insertValueSearch(arr, midIndex + 1, right, key);} else if (key < midVal) {// 向左掃描遞歸return insertValueSearch(arr, left, midIndex - 1, key);} else {return midIndex;}}

總結

• 對于數據量較大，關鍵字分布比較均勻的查找表來說，采用插值查找，速度較快
• 關鍵字分布不均勻的情況下，該方法不一定比折半查找要好

---

斐波那契查找（黃金分割法）

需要數組是有序

• 黃金分割點是指把一條線段分割為兩部分，使其中一部分與全長之比等于另一部分與這部分之比。取其前三位數字的近似值是0.618。由于按此比例設計的造型十分美麗，因此稱為黃金分割，也稱為中外比。這是一個神奇的數字，會帶來意向不大的效果。
• 斐波那契數列{1,1,2,3,5,8,13,21,34,55}發現斐波那契數列的兩個相鄰數的比例，無限接近黃金分割值0.618

原理

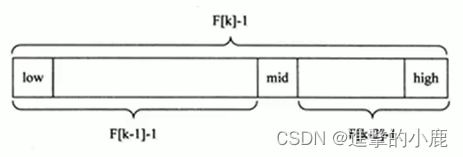
斐波那契查找原理與前兩種相似，僅僅改變了中間結點(mid)的位置，mid不再是中間或插值得到，而是位于黃金分割點附近，即$mid=low+F(k?1)?1$ (F代表斐波那契數列。k代表斐波那契個數)

對F(k-1)-1的理解：

• 由斐波那契數列$F[K]=F[k?1]+F[k?2]$的性質，可以得到$(F[k]?1)=(F[k?1]?1)+(F[k?2]?1)+1$
  該式說明：只要順序表的長度為$F[k]?1$，則可以將該表分成長度為$F[k?1]?1$和$F[k?2]?1$的兩段，從而中間位置為$mid=low+F(k?1)?1$

• 類似的，每一子段也可以用相同的方式分割

• 但順序表長度$n$不一定剛好等于$F[K]?1$，所以需要將原來的順序表長度n增加至$F[K]?1$。這里的$k$值只要能使得$F[k]?1$恰好大于或等于$n$即可，由以下代碼得到，順序表長度增加后，新增的位置（從$n+1$到$F[K]?1$位置)，都賦為$n$位置的值即可。

  while (high > f[k] - 1) {// 如果大于，則k++k++;
  }
  

注意：因為黃金分割點是第三段的前一段除以整段，之所以減1是因為數組是從0開始，所以$F[k]?1=(F[k?1]?1)+(F[k?2]?1)+分割點$，第三點，由于f(k) 有可能小于n（也就是high），就不滿足斐波那契數列要求

// 使用非遞歸方法得到一個斐波那契數列
public static int maxSize = 20;// 后面需要mid=low+F(k-1)-1，因此先獲取一個斐波那契數列
public static int[] fib() {int[] f = new int[maxSize];f[0] = 1;f[1] = 1;for (int i = 2; i < maxSize; i++) {f[i] = f[i - 1] + f[i - 2];}return f;
}// 斐波那契查找 --- 非遞歸
// key為需要查找的關鍵碼(值)
public static int fibSearch(int[] a, int key) {int low = 0;int high = a.length - 1;int k = 0; // 表示斐波那契分割數值的下標int mid = 0; // 存放a數組分割點int[] f = fib(); // 獲取到斐波那契數列// 獲取到斐波那契分割數值的下標// f[k] - 1 為臨時數組的長度，不得小于a數組的長度while (high > f[k] - 1) {// 如果大于，則k++k++;}// f[k] 可能大于a 的長度，因此需要使用Arrays類構造一個新的數組，并指向temp[]// 不足的部分會使用0填充int[] temp = Arrays.copyOf(a, f[k]);// 實際上需要使用a數組的數填充temp// temp = {1, 8, 10, 80, 1000, 0, 0, 0} => {1, 8, 10, 80, 1000, 1000, 1000, 1000}for (int i = high + 1; i < temp.length; i++) {temp[i] = a[high];}// 使用while 來循環處理找到我們的數keywhile (low <= high) {mid = low + f[k - 1] - 1;if (key < temp[mid]) {// 向左邊查找high = mid - 1;// f[k] = f[k-1] + f[k-2]，之后f[k-1]繼續拆分，因此k--k--;} else if (key > temp[mid]) { // 向右查找low = mid + 1;// f[k] = f[k-1] + f[k-2]，之后f[k-2]繼續拆分// f[k-1] = f[k-3] + f[k-4]，因此k -=2k -= 2;} else {// 找到if (mid <= high) {return mid;} else {return high;}}}return -1;
}