學習參考：

• 動手學深度學習2.0
• Deep-Learning-with-TensorFlow-book
• pytorchlightning

①如有冒犯、請聯系侵刪。
②已寫完的筆記文章會不定時一直修訂修改(刪、改、增)，以達到集多方教程的精華于一文的目的。
③非常推薦上面（學習參考）的前兩個教程，在網上是開源免費的，寫的很棒，不管是開始學還是復習鞏固都很不錯的。

深度學習回顧，專欄內容來源多個書籍筆記、在線筆記、以及自己的感想、想法，佛系更新。爭取內容全面而不失重點。完結時間到了也會一直更新下去，已寫完的筆記文章會不定時一直修訂修改(刪、改、增)，以達到集多方教程的精華于一文的目的。所有文章涉及的教程都會寫在開頭、一起學習一起進步。

一、數值穩定性的重要性

到目前為止，實現的每個模型都是根據某個預先指定的分布來初始化模型的參數。

有人會認為初始化方案是理所當然的，忽略了如何做出這些選擇的細節。甚至有人可能會覺得，初始化方案的選擇并不是特別重要。

相反，初始化方案的選擇在神經網絡學習中起著舉足輕重的作用， 它對保持數值穩定性至關重要。 此外，這些初始化方案的選擇可以與非線性激活函數的選擇有趣的結合在一起。 選擇哪個函數以及如何初始化參數可以決定優化算法收斂的速度有多快。 糟糕選擇可能會導致我們在訓練時遇到梯度爆炸或梯度消失。

考慮一個具有 𝐿 層、輸入 𝐱和輸出 𝐨的深層網絡。 每一層 𝑙由變換 𝑓𝑙定義， 該變換的參數為權重 𝐖(𝑙) ， 其隱藏變量是 𝐡(𝑙)（令 𝐡(0)=𝐱）。 網絡可以表示為：

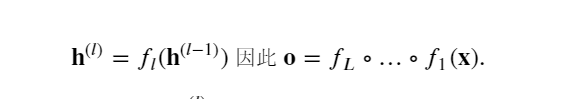
如果所有隱藏變量和輸入都是向量， 可以將 𝐨關于任何一組參數 𝐖(𝑙) 的梯度寫為下式，該梯度是 𝐿?𝑙 個矩陣 𝐌(𝐿)?…?𝐌(𝑙+1) 與梯度向量 𝐯(𝑙) 的乘積。

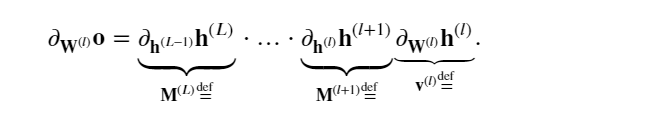
因此，上面公式計算的結果容易受到數值下溢問題的影響. 當將太多的概率乘在一起時，這些問題經常會出現。 在處理概率時，一個常見的技巧是切換到對數空間， 即將數值表示的壓力從尾數轉移到指數。 不幸的是，上面的問題更為嚴重： 最初，矩陣 𝐌(𝑙) 可能具有各種各樣的特征值。 他們可能很小，也可能很大； 他們的乘積可能非常大，也可能非常小。

不穩定梯度帶來的風險不止在于數值表示； 不穩定梯度也威脅到優化算法的穩定性。

可能面臨一些問題：

• 梯度爆炸（gradient exploding）問題： 參數更新過大，破壞了模型的穩定收斂；
• 梯度消失（gradient vanishing）問題： 參數更新過小，在每次更新時幾乎不會移動，導致模型無法學習。

二、梯度消失

在深度神經網絡中，梯度消失指的是在反向傳播過程中，梯度逐漸變小并接近零，導致較深層的網絡參數無法得到有效更新，從而影響模型的訓練效果。

梯度消失通常發生在使用激活函數導數具有較小值的情況下，尤其是在使用 sigmoid 或 tanh 激活函數時。

sigmoid函數 1/(1+exp(?𝑥))很流行， 因為它類似于閾值函數。 由于早期的人工神經網絡受到生物神經網絡的啟發， 神經元要么完全激活要么完全不激活（就像生物神經元）的想法很有吸引力。 然而，它卻是導致梯度消失問題的一個常見的原因。下圖是sigmoid函數變化圖和梯度變化圖。

%matplotlib inline
import tensorflow as tf
from d2l import tensorflow as d2lx = tf.Variable(tf.range(-8.0, 8.0, 0.1))
with tf.GradientTape() as t:y = tf.nn.sigmoid(x)
d2l.plot(x.numpy(), [y.numpy(), t.gradient(y, x).numpy()],legend=['sigmoid', 'gradient'], figsize=(4.5, 2.5))

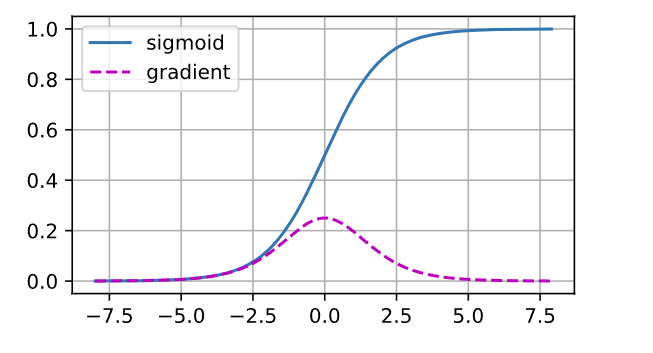
當sigmoid函數的輸入很大或是很小時，它的梯度都會消失。 此外，當反向傳播通過許多層時，除非在剛剛好的地方， 這些地方sigmoid函數的輸入接近于零，否則整個乘積的梯度可能會消失。 當網絡有很多層時，除非很小心，否則在某一層可能會切斷梯度。

事實上，這個問題曾經困擾著深度網絡的訓練。 因此，更穩定的ReLU系列函數已經成為從業者的默認選擇（雖然在神經科學的角度看起來不太合理）。

三、梯度爆炸

梯度爆炸則是指在反向傳播過程中，梯度變得非常大，超過了數值范圍，導致參數更新過大，模型無法穩定訓練。

梯度爆炸通常出現在網絡層數較多、權重初始化不當或者學習率設置過高的情況下。

相反，梯度爆炸可能同樣令人煩惱。 為了更好地說明這一點，生成100個高斯隨機矩陣，并將它們與某個初始矩陣相乘。 對于我們選擇的尺度（方差 𝜎2=1 ），矩陣乘積發生爆炸。 當這種情況是由于深度網絡的初始化所導致時，導致沒有機會讓梯度下降優化器收斂。

M = tf.random.normal((4, 4))
print('一個矩陣 \n', M)
for i in range(100):M = tf.matmul(M, tf.random.normal((4, 4)))print('乘以100個矩陣后\n', M.numpy())

一個矩陣 tf.Tensor(
[[ 3.7436965   2.652792    0.5994665  -0.17366047][ 0.6720035  -0.7297903   0.3705189  -0.5043682 ][ 0.53814566 -0.94948226  0.09689955 -0.4441989 ][ 0.6737587   0.41651404 -0.9230542   0.1903977 ]], shape=(4, 4), dtype=float32)
乘以100個矩陣后[[-1.9263415e+26  1.5658991e+27  3.4174752e+26 -9.1476850e+25][ 1.4916346e+24 -1.2148971e+25 -2.6495698e+24  7.0983965e+23][ 2.5503458e+25 -2.0726612e+26 -4.5202026e+25  1.2112884e+25][ 1.2258523e+25 -9.9649782e+25 -2.1730161e+25  5.8238054e+24]]

四、解決梯度消失和梯度爆炸的方法

• 梯度裁剪（Gradient Clipping）：限制梯度的大小，防止梯度爆炸。
• 使用恰當的激活函數：如 ReLU 可以緩解梯度消失問題。
• 參數初始化：使用合適的參數初始化方法，如 Xavier 或 He 初始化。
• 批歸一化（Batch Normalization）：通過規范化每層輸入，有助于緩解梯度消失和梯度爆炸問題。
• 殘差連接（Residual Connections）：在深層網絡中使用殘差連接有助于減輕梯度消失問題。

五、模型參數初始化

解決（或至少減輕）上述問題（梯度消失、梯度爆炸）的一種方法是進行參數初始化， 優化期間的注意和適當的正則化也可以進一步提高穩定性。

選擇適當的參數初始化方法取決于網絡的結構、激活函數的選擇以及具體任務的要求。良好的參數初始化可以幫助加速模型的收斂速度，提高模型的性能，并有助于避免梯度消失和梯度爆炸等問題。

1.默認初始化

使用正態分布來初始化權重值。如果不指定初始化方法， 框架將使用默認的隨機初始化方法，對于中等難度的問題，這種方法通常很有效。

2.Xavier初始化

Xavier初始化（Xavier Initialization）：也稱為Glorot初始化，根據輸入和輸出的神經元數量來初始化參數。這種方法旨在使每一層的激活值保持在一個合理的范圍內，有助于避免梯度消失和梯度爆炸問題。

3.He初始化（He Initialization）

與Xavier初始化類似，但是在計算方差時只考慮了輸入神經元的數量，適用于使用ReLU激活函數的網絡。

4.正交初始化（Orthogonal Initialization）

通過生成一個正交矩陣來初始化權重，有助于避免梯度消失和梯度爆炸問題。

5.自適應方法（Adaptive Methods）

如自適應矩估計（Adagrad）、RMSProp、Adam等優化算法，這些算法在訓練過程中會自動調整學習率，有助于更好地初始化參數。

6.其它

深度學習框架通常實現十幾種不同的啟發式方法。 此外，參數初始化一直是深度學習基礎研究的熱點領域。 其中包括專門用于參數綁定（共享）、超分辨率、序列模型和其他情況的啟發式算法。