Multimodal Instruction Tuning with Conditional Mixture of LoRA
公和眾和號:EDPJ(進 Q 交流群:922230617 或加 VX:CV_EDPJ 進 V 交流群)
目錄
0. 摘要
3. 任務干擾在多模態指令調優中的 LoRA 應用
3.1 背景:LoRA
3.2 調查多模態指導調優中的任務干擾
4. 條件 LoRA 混合
4.1 動態因子選擇
4.1.1 獨立因子選擇
4.1.2 條件因子選擇
4.1.3 動態自適應矩陣的重建
5. 實驗
0. 摘要
多模態大型語言模型(MLLMs)在不同領域的各種任務中展現了出色的熟練性,越來越關注提高它們在看不見的多模態任務上的 zero-shot 泛化能力。多模態指令調優已成為通過指令在各種多模態任務上對預訓練模型進行微調以實現 zero-shot 泛化的成功策略。隨著 MLLMs 的復雜性和規模的增加,對于像低秩適應(Low-Rank Adaption,LoRA)這樣的參數高效的微調方法的需求變得至關重要,該方法通過使用最小的參數集進行微調。
然而,在多模態指令調優中應用 LoRA 面臨任務干擾的挑戰,這導致性能下降,尤其是在處理廣泛的多模態任務時。為了解決這個問題,本文介紹了一種新方法,將多模態指令調優與條件 LoRA 混合(Mixture-of-LoRA,MixLoRA)相結合。它通過動態構建適應于每個輸入實例獨特需求的低秩適應矩陣,來減輕任務干擾。對各種多模態評估數據集的實驗證明,MixLoRA 不僅在相同或更高秩的情況下勝過傳統的 LoRA,展示了其在各種多模態任務中的功效和適應性。
3. 任務干擾在多模態指令調優中的 LoRA 應用
3.1 背景:LoRA
3.2 調查多模態指導調優中的任務干擾
我們的研究深入探討了在參數高效的多模態指令調優中分析任務對之間梯度方向沖突的任務干擾。對于每一對任務 i 和 j,我們首先估計在根據任務 j 的損失 Lj 優化共享參數 θ 時,任務 i 的損失 Li 的變化,遵循(Zhu等,2022):
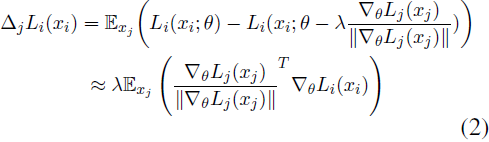
其中,xi 和 xj 是任務 i 和 j 的采樣訓練 batch,λ 是學習率。然后,任務 j 對任務 i 的干擾被量化如下:

在這里,正的 I_(i,j)? 表明任務 i 和 j 之間的梯度方向是對齊的,而負值意味著梯度方向是分離的,表明任務 j 對任務 i 產生不利影響。
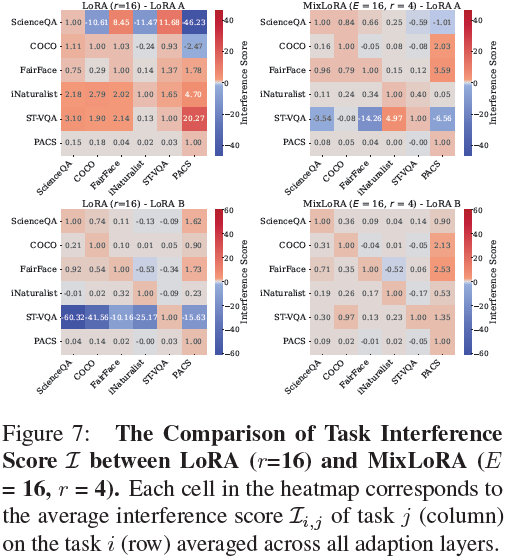
我們在使用 LoRA 和秩為 4 進行微調的 LLaVa(Liu等,2023)模型上進行實驗,計算來自 Vision-Flan(Xu等,2023a)的六個不同任務之間的任務干擾,包括 “ScienceQA”(Lu等,2022)(用于“復雜推理”),“COCO”(Lin等,2014)(用于“粗粒度感知”),“Fair-Face”(Karkkainen和Joo,2021)(用于“細粒度感知”),“iNaturalist”(Van Horn等,2018)(用于“知識密集型”),“STVQA”(Biten等,2019)(用于“OCR”),以及 “PACS”(Li等,2017)(用于“領域特定”)。

我們基于涉及 LoRA A 和 B 的梯度計算任務干擾矩陣 I 的平均值,跨越各個層次。圖 2 顯示了 MLP(圖 2a) 和 Self-Attention(圖 2b) 在第 5 層和第 25 層 Transformer 層的 LoRA A 和 B 的任務干擾分數。
我們的結果顯示,對于 LoRA A 和 B,無論在淺層還是深層 Transformer 層,都存在顯著的任務干擾。例如,如圖 2b 所示,在第 5 層的 LoRA A 中,領域特定的分類任務 “PACS” 對粗粒度感知任務 “COCO” 產生負面影響,負干擾分數為 -7.3。與此同時,還觀察到了正面的影響。例如,圖 2a 顯示,在 LoRA B 的第 5 層,“PACS” 對 OCR 任務 “ST-VQA” 產生積極影響。正面和負面干擾的存在表明指導任務之間存在復雜的動態:正分數(紅色)表明一個任務的學習可以增強另一個任務的性能,而負分數(藍色)則意味著一個任務的學習可能會妨礙另一個任務。這些發現突顯了在參數高效的多模態指導調優中存在顯著的任務干擾,并強調了需要有效的適應方法來確保在各種多模態任務中具有強大和多功能的性能。
4. 條件 LoRA 混合
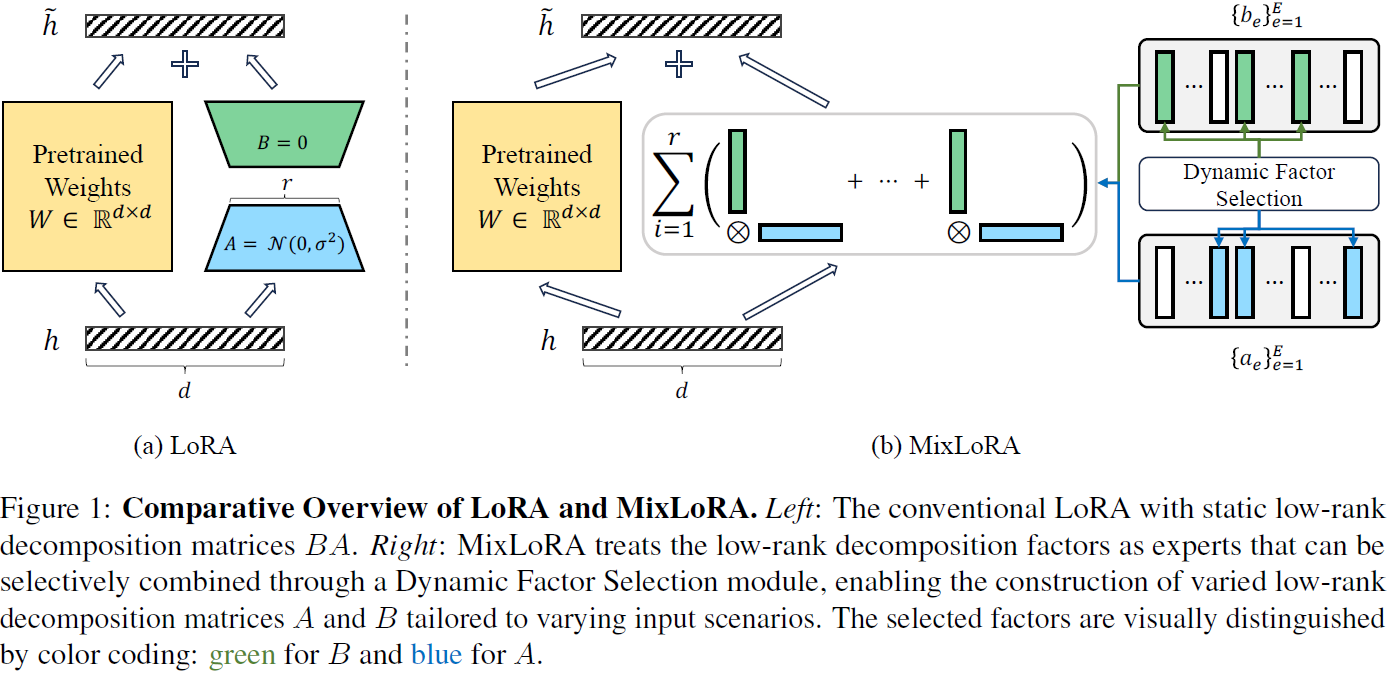
受到 “專家混合” 概念的啟發(Shazeer等,2016),我們提出了條件 LoRA 混合(MixLoRA),它利用低秩分解因子(low-rank decomposition factors)作為動態選擇的專家,構建針對特定輸入實例的定制分解矩陣 A 和 B。MixLoRA 促進了對不同輸入實例的動態處理路徑,從而增強了處理各種復雜多模態指導任務的效力。
條件LoRA混合的核心在于通過張量分解表示權重調整矩陣 ΔW:

其中 {ai, bi} 是 ΔW 的秩 r 分解因子,ai ∈ R^(d_in × 1),bi ∈ R^(d_out × 1)。
利用 ΔW 可以表示為低秩分解因子 ai 和 bi 外積之和的概念,MixLoRA 引入了一個動態因子選擇(Dynamic Factor Selection)模塊。該模塊通過從擴展的分解因子池
![]()
中選擇 r 個適當的因子,動態構建特定輸入的唯一 ΔW,如圖 1(b)所示。
4.1 動態因子選擇
動態因子選擇模塊使用兩個主要組件來動態構建 LoRA A 和 B。首先,兩個獨立因子選擇(Independent Factor Selection,IFS)路由器(第 4.1.1 節)分別選擇 r 個相關因子,形成適應矩陣 LoRA A 和 B,確保精確、針對實例的自適應。其次,一個條件因子選擇(Conditional Factor Selection,CFS)路由器(第 4.1.2 節)通過在選擇 LoRA B 時將選擇 B 的因子以選擇 LoRA A 的因子為條件,推動了一致的自適應過程。
4.1.1 獨立因子選擇
MixLoRA 采用兩個獨立因子選擇(IFS)路由器,
![]()
分別選擇 LoRA A 和 B 的 r 個相關因子,如圖 3 所示。

IFS 路由器采用基于實例的路由方法,相對于基于傳統輸入 token 的路由,這更具內存效率,用于選擇 r 個分解因子。路由策略可以表示為:
![]()
其中 Avg(·) 對前一層的隱藏狀態 h ∈ R^(seq × d_in) 在序列維度上進行平均。
因子選擇過程涉及計算向量 gA∈R^E 和 gB∈R^E,以選擇從集合 {a_e?}^E_(e=1?) 和 {a_e?}^E_(e=1?)? 中的特定子集,分別用于 LoRA A 和 B。為了計算 gA,輸入
![]()
通過具有權重 W_A ∈ R_(E × d_in) 的稠密層(dense layer)進行處理,然后進行 softmax 歸一化和 top-r 選擇:
![]()
該過程確保選擇 LoRA A 的 r 個因子,其中 g_A[i] = 1 表示選擇因子 i。相同的過程應用于確定 LoRA B 的 gB。
4.1.2 條件因子選擇
盡管到目前為止 LoRA A 和 B 的因子是獨立選擇的,但我們假設 LoRA A 和 B 的選擇之間存在相互依賴關系,可以利用這種關系提高模型的整體適應性和性能。為了利用這種關系,我們提出了一種條件因子選擇(Conditional Factor Selection,CFS)策略,其中 LoRA B 投影上權重的因子選擇也受到了為 LoRA A 投影下權重選擇的因子的影響。
通過 IFS 路由器,LoRA A 從選擇的分解因子中組裝而成,表示為 A = [a1, · · · , ar]?,其中 A ∈ ?^(r x d_in)。在這之后,CFS 路由器采用權重張量 W_AB ∈ ?^(r x d_in x E),將 A 中的每個因子 A[i] ∈ ?^(r x d_in) 映射到專家維度 𝔼。對于每個因子 A[i],通過 softmax 歸一化并在 r 個因子上聚合的映射過程如下:
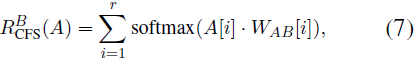
其中 W_AB[i] ∈ ?^(d_in x E) 是與 A[i] 相關的映射矩陣。
LoRA B 的因子選擇集成了 IFS RB IFS(·) 和 CFS RB CFS(·) 路由器的輸出,通過后融合(late fusion)策略形成選擇向量 gB,具體如下:
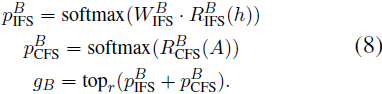
最終選擇向量 gB 由來自 IFS 和 CFS 路由器的概率分布 p^B_IFS?和 p^B_CFS?組合而成。這種 CFS 策略使得 LoRA B 的選擇能夠受到為 LoRA A 選擇的因子的啟發,促使一個更具連貫性的選擇過程。
4.1.3 動態自適應矩陣的重建
最后,MixLoRA 通過利用因子選擇向量 gA 和 gB,收集已選因子 a?、b? ∈ 𝕂,|𝕂| = r,以組裝 LoRA A 和 B 的最終矩陣,從而構建動態自適應矩陣。因此,在每次前向傳遞中,基于這些已選擇的因子動態計算權重調整矩陣 ΔW ∈ ?????×???,表示為:
![]()
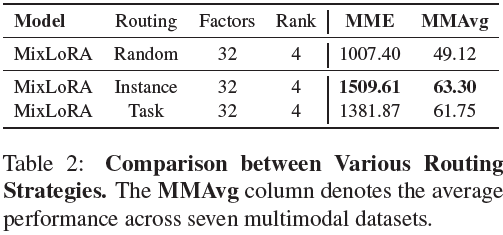
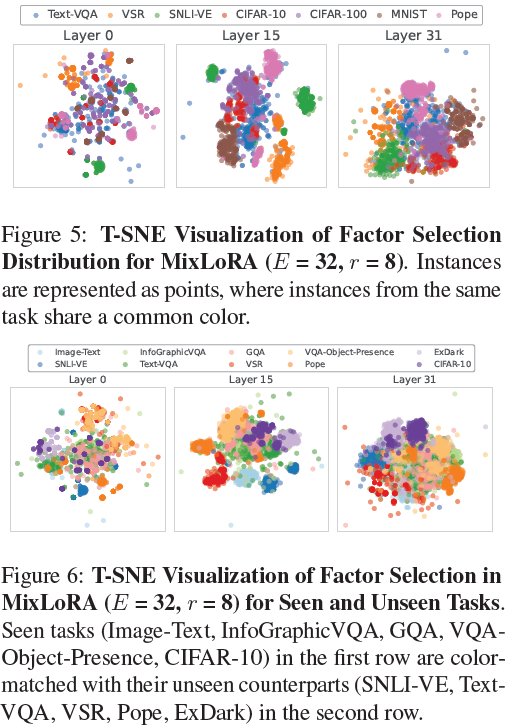
5. 實驗



?










【數據持久化(用戶首選項、關系型數據庫)、通知(基礎通知、進度條通知、通知意圖)】)






Windows系統---保姆級教程)

)