AVL 樹

AVL樹的概念

二叉搜索樹雖可以縮短查找的效率，但如果數據有序或接近有序二叉搜索樹將退化為單支樹，查找元素相當于在順序表中搜索元素，效率低下。因此，兩位俄羅斯的數學家G.M.Adelson-Velskii和E.M.Landis在1962年
發明了一種解決上述問題的方法：當向二叉搜索樹中插入新結點后，如果保證每個結點的左右子樹高度之差的絕對值不超過1(需要對樹中的結點進行調整)，即可降低樹的高度，從而減少平均搜索長度。

一棵AVL樹或者是空樹，或者是具有以下性質的二叉搜索樹：

它的左右子樹都是AVL樹
左右子樹高度之差(簡稱平衡因子)的絕對值不超過1(-1/0/1)

節點的平衡因子=右子樹的高度-左子樹的高度

例如：
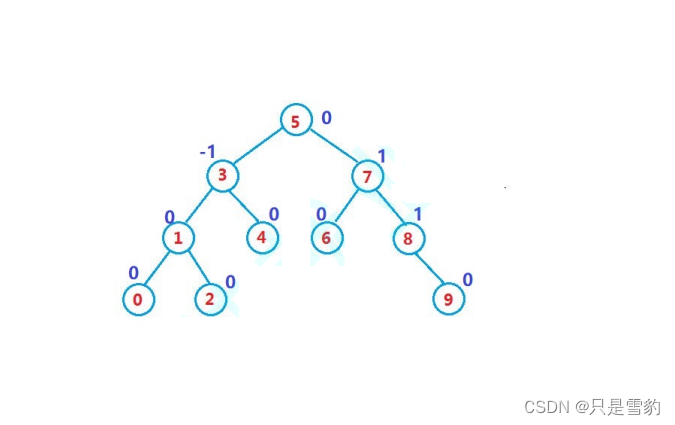
下圖的二叉搜索樹的每個節點的平衡因子的絕對值都小于2，并且每個節點的子樹也都是AVL樹
在這里插入圖片描述

AVL樹的定義

AVL樹是一種特殊的二叉搜索樹，它具有高度的平衡，所以為了在插入過程中的各個節點的平衡因子的更新，我們在定義AVL樹的節點結構的同時要帶上一個節點的雙親結點parent

template<class T>
struct AVLTreeNode
{AVLTreeNode(const T& data): _left(nullptr), _right(nullptr), _parent(nullptr), _data(data), _bf(0){}AVLTreeNode<T>* _left;   // 該節點的左孩子AVLTreeNode<T>* _right;  // 該節點的右孩子AVLTreeNode<T>* _parent; // 該節點的雙親T _data;int _bf;                  // 該節點的平衡因子
};

AVL樹的插入

AVL樹的插入是一個難點，它分為好幾種情況，其實AVL樹的插入也就是在二叉搜索樹中插入新節點，但是由于他引入了平衡因子，需要更新，所以這里的插入節點就比較麻煩，她一共分為兩步：

1 插入節點
2 更新節點的平衡因子

為什么要更新節點的平衡因子呢？

簡單地舉個例子：
如圖所示，我將一個新節點插入0的左孩子節點的位置，那么以3為節點的這顆子樹的高度差不就會超過1了嗎，他的左子樹的高度插入新節點后為3，而右子樹為1，這就不符合AVL樹的性質了，所以我們需要經過一些操作來更新平衡因子
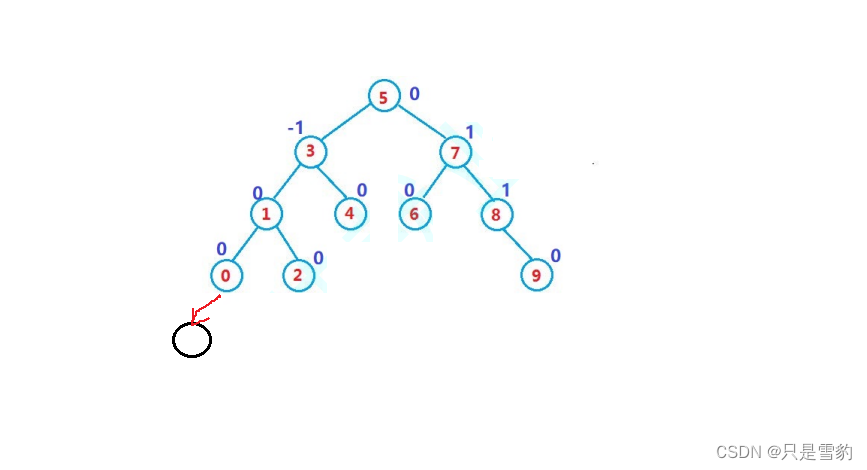
在這里插入圖片描述

這里大家需要注意一個規則：
新節點如果是插入后他的parent的左側，那么他的平衡因子默認是+1
反之插入他的右側就是默認-1

那么在插入節點后，各個插入節點的parent一共就有三種情況了：

平衡因子為0
如果parent的平衡因子為0，說明插入之前parent的平衡因子為正負1，插入后被調整成0，此時滿足AVL樹的性質，插入成功

平衡因子為正負1
如果parent的平衡因子為正負1，說明插入前pParent的平衡因子一定為0，插入后被更新成正負1，此時以parent為根的樹的高度增加，需要繼續向上更新，防止部分節點的左右子樹高度差超過1
平衡因子為正負2
如果parent的平衡因子為正負2，則pParent的平衡因子違反平衡樹的性質，需要對其進行旋轉處理，旋轉處理之后插入成功

至于旋轉的情況我們待會分析，我們先將插入節點的代碼的主要框架構造出來：
這樣一個簡單的框架就構造出來了

template<class T>
struct AVLTreeNode
{AVLTreeNode<T>* _left;   // 該節點的左孩子AVLTreeNode<T>* _right;  // 該節點的右孩子AVLTreeNode<T>* _parent; // 該節點的雙親T _data;int _bf;                  // 該節點的平衡因子AVLTreeNode(const T& data): _left(nullptr), _right(nullptr), _parent(nullptr), _data(data), _bf(0){}
};
template<class T>
class AVLTree
{typedef AVLTreeNode<T> Node;
public:bool insert(const T& data){if (_root == nullptr){_root = new Node(data);return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_data < data){parent = cur;cur = cur->_right;}else if (cur->_data > data){parent = cur;cur = cur->_left;}else{return false;}cur = new Node(data);if (parent->_data > data){parent->_left = cur;}else{parent->_right = cur;}while (parent){//左邊++if (cur == parent->_left){parent->_bf--;}//右邊--else{parent->_bf++;}//parent的平衡因子等于0，插入成功if (parent->_bf == 0){break;}//parent的平衡因子等于1或者-1，繼續向上更新else if (parent->_bf == 1 || parent->_bf == -1){cur = parent;parent = parent->_parent;}else if (parent->_bf == 2 || parent->_bf == -2){//需要進行旋轉}else{assert(false);}}}}private:Node* _root;
};

下面我們就具體分析幾種旋轉的情況

AVL樹的旋轉

如果在一棵原本是平衡的AVL樹中插入一個新節點，可能造成不平衡，此時必須調整樹的結構，使之平衡化。根據節點插入位置的不同，AVL樹的旋轉分為四種：

1. 新節點插入較高左子樹的左側—左左：右單旋
下圖中的h可以時0 1 2三種，分別代表了這三個子樹的高度，無論他是等于0 1 還是2時他們都可以滿足AVL樹的要求
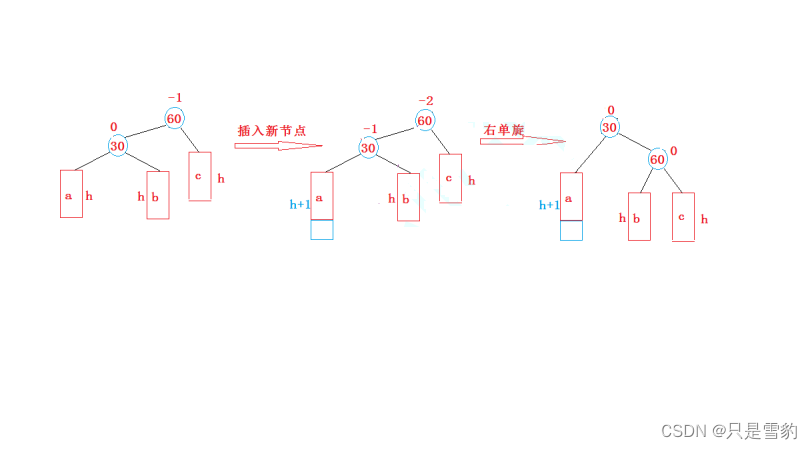
在這里插入圖片描述
可以看到，這種情況就是parent的平衡因子等于-2，cur的平衡因子等于-1
左旋函數如下：

void RotateR(Node* parent)
{Node* subL = parent->_left;Node* subLR = subL->_right;parent->_left = subLR;//防止sublr為空if(subLR)subLR->_parent = parent;//記錄祖父位置Node* pparent = parent->_parent;subL->_right = parent;parent->_parent = subL;//如果父親是根節點if (parent == _root){_root = subL;subL->_parent = nullptr;}//parent不是根節點，那么祖父就會成為subl的parentelse{if (pparent->_left == parent){pparent->_left = subL;subL->_parent = pparent;}else{pparent->_right = subL;subL->_parent = pparent;}}//旋轉后parent和subl的 平衡因子都會更新為0parent->_bf = subL->_bf = 0;
}

2. 新節點插入較高右子樹的右側—右右：左單旋
實現及情況考慮可參考右單旋。
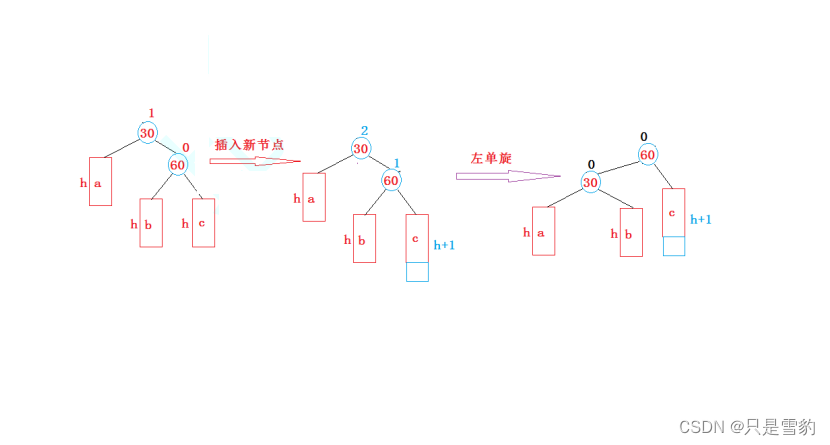
在這里插入圖片描述

void RotateL(Node* parent)
{Node* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;subR->_left = parent;Node* pparent = parent->_parent;if (subRL)subRL->_parent = parent;if (_root == parent){_root = subR;subR->_parent == nullptr;}else{if (pparent->_left == parent){pparent->_left = subR;subR->_parent = pparent;}else{pparent->_right = subR;subR->_parent = pparent;}}parent->_bf = subR->_bf = 0;
}

3. 新節點插入較高左子樹的右側—左右：先左單旋再右單旋
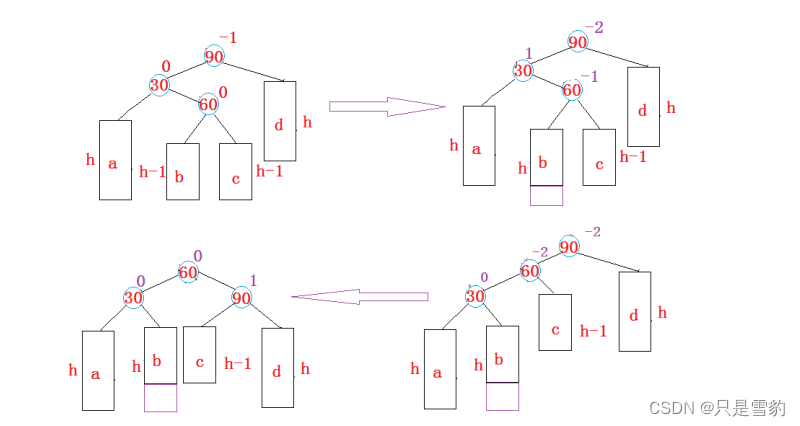
在這里插入圖片描述
將雙旋變成單旋后再旋轉，即：先對30進行左單旋，然后再對90進行右單旋，旋轉完成后再考慮平衡因子的更新。
直接復用即可：
由于博主能力有限，所以放入代碼大家仔細理解

void RotateLR(Node* parent)
{Node* subL = parent->_left;Node* subLR = subL->_right;RotateL(parent->_left);RotateR(parent);int bf = subLR->_bf;//sublr就是新增節點if (bf == 0){parent->_bf = 0;subL->_bf = 0;subLR->_bf = 0;}//sublr左子樹新增節點else if (bf == -1){parent->_bf = 1;subL->_bf = 0;subLR->_bf = 0;}//sublr右子樹新增節點else if (bf == 1){parent->_bf = 0;subL->_bf = -1;subLR->_bf = 0;}else{assert(false);}
}

4. 新節點插入較高右子樹的左側—右左：先右單旋再左單旋
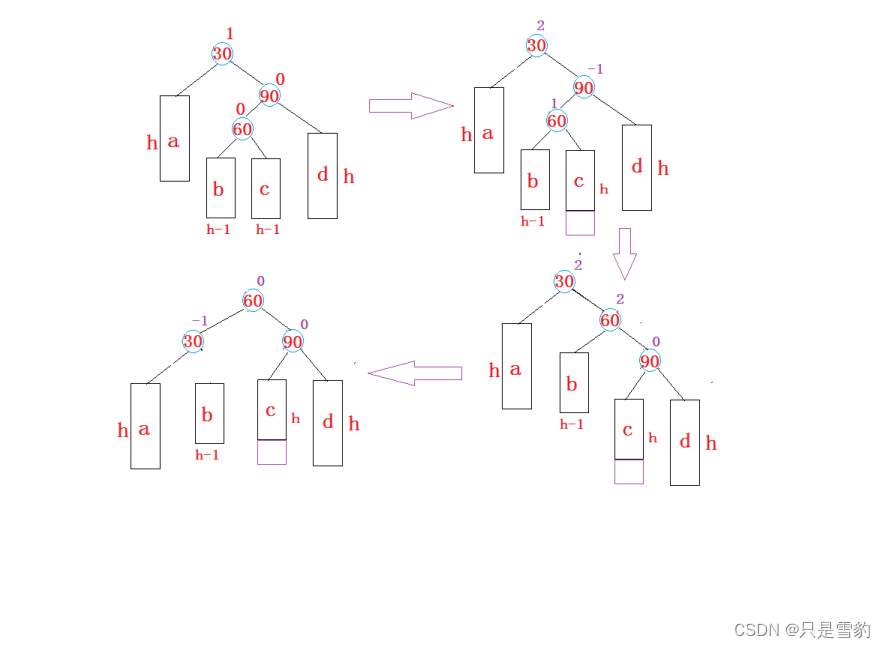
在這里插入圖片描述

void RotateRL(Node* parent)
{Node* subR = parent->_right;Node* subRL = subR->_left;int bf = subRL->_bf;RotateR(parent->_right);RotateL(parent);//subrl這個點為新增點if (bf == 0){parent->_bf = subR->_bf = subRL->_bf = 0;}//subrl的左子樹新增else if (bf == -1){parent->_bf = 0;subRL->_bf = 0;subR->_bf = 1;}//subrl的右子樹新增else if (bf == 1){parent->_bf = -1;subRL->_bf = 0;subR->_bf = 0;}else{assert(false);}
}

根據各種情況我們做了總結：

假如以parent為根的子樹不平衡，即parent的平衡因子為2或者-2，分以下情況考慮

parent的平衡因子為2，說明parent的右子樹高，設parent的右子樹的根為subR，當subR的平衡因子為1時，執行左單旋當subR的平衡因子為-1時，執行右左雙旋
parent的平衡因子為-2，說明parent的左子樹高，設parent的左子樹的根為subL，當subL的平衡因子為-1是，執行右單旋，當subL的平衡因子為1時，執行左右雙旋旋轉完成后，原parent為根的子樹個高度降低，已經平衡，不需要再向上更新。

所以我們可以補全上面的插入節點的代碼了：

bool insert(const T& data)
{if (_root == nullptr){_root = new Node(data);return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_data < data){parent = cur;cur = cur->_right;}else if (cur->_data > data){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(data);if (parent->_data > data){parent->_left = cur;}else{parent->_right = cur;}while (parent){//左邊++if (cur == parent->_left){parent->_bf--;}//右邊--else{parent->_bf++;}//parent的平衡因子等于0，插入成功if (parent->_bf == 0){break;}//parent的平衡因子等于1或者-1，繼續向上更新else if (parent->_bf == 1 || parent->_bf == -1){cur = parent;parent = parent->_parent;}else if (parent->_bf == 2 || parent->_bf == -2){//需要進行旋轉if (parent->_bf == 2 && cur->_bf == 1){RotateL(parent);}else if (parent->_bf == 2 && cur->_bf == -1){RotateRL(parent);}else if (parent->_bf == -2 && cur->_bf == -1){RotateR(parent);}else if (parent->_bf == -2 && cur->_bf == 1){RotateLR(parent);}break;}else{assert(false);}}return true;
}

AVL樹的驗證

AVL樹是在二叉搜索樹的基礎上加入了平衡性的限制，因此要驗證AVL樹，可以分兩步：

1. 驗證其為二叉搜索樹
如果中序遍歷可得到一個有序的序列，就說明為二叉搜索樹
2. 驗證其為平衡樹每個節點子樹高度差的絕對值不超過1(注意節點中如果沒有平衡因子)節點的平衡因子是否計算正確

我們可以用一個函數來判斷即可：
首先要有一個計算樹的高度的函數
然后判斷他們的子樹的高度差的絕對值是否在2以內，并且他們的子樹也要是AVL樹

int Height(Node* root)
{if (root == nullptr){return 0;}int leftheight = Height(root->_left);int rightheight = Height(root->_right);return leftheight > rightheight ? leftheight + 1 : rightheight + 1;
}bool isbalance()
{return _isbalance(_root);
}bool _isbalance(Node* root)
{if (root == nullptr)return true;int leftheight = Height(root->_left);int rightheight = Height(root->_right);if (rightheight - leftheight != root->_bf){cout << root->_data << "平衡因子異常" << endl;return false;}return abs(rightheight - leftheight) < 2&& _isbalance(root->_left)&& _isbalance(root->_right);
}

我們還可以用中序遍歷打印：

void inorder()
{_inorder(_root);cout << endl;
}void _inorder(Node* root)
{if (root == nullptr){return;}_inorder(root->_left);cout << root->_data << " ";_inorder(root->_right);
}

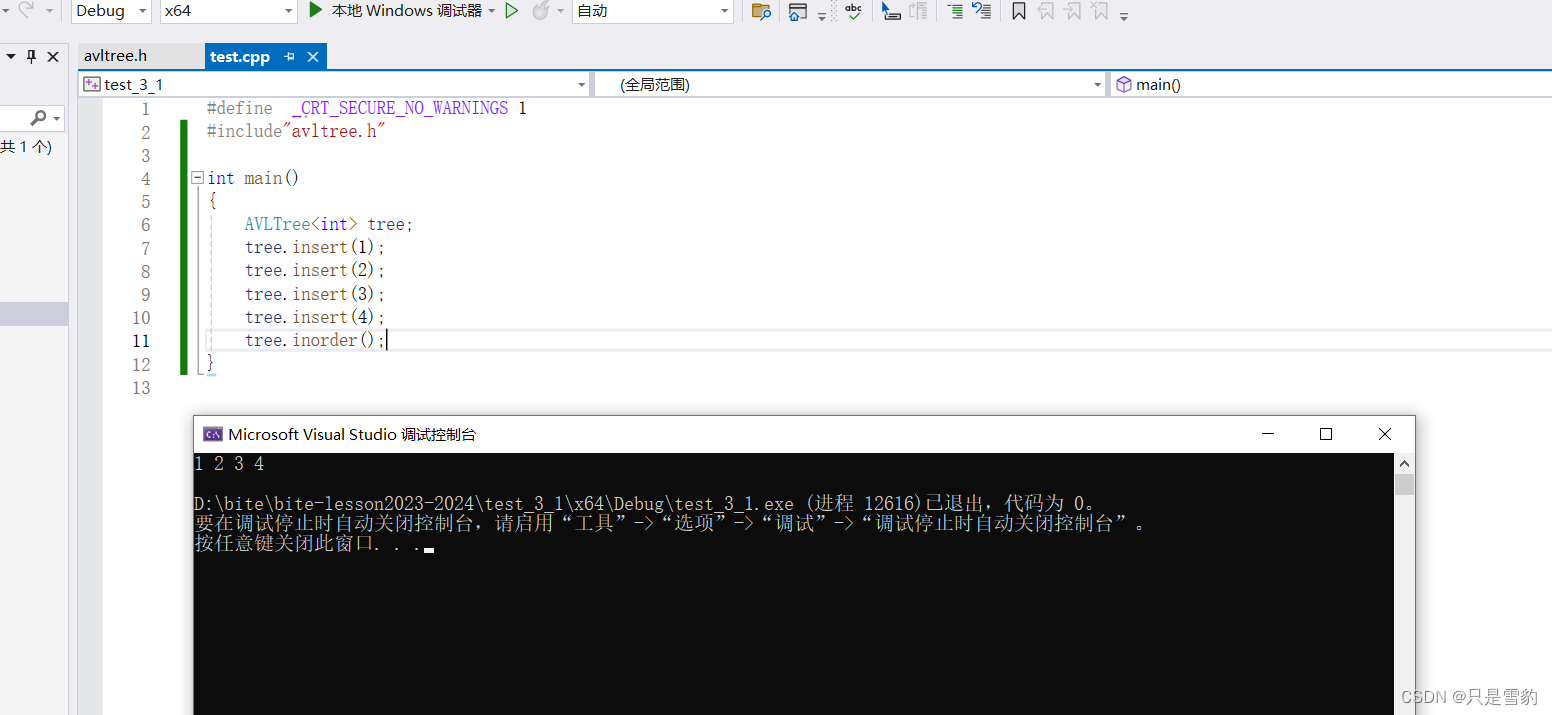
在這里插入圖片描述
完整代碼如下：

#include<iostream>
#include<assert.h>
using namespace std;
template<class T>
struct AVLTreeNode
{AVLTreeNode<T>* _left;   // 該節點的左孩子AVLTreeNode<T>* _right;  // 該節點的右孩子AVLTreeNode<T>* _parent; // 該節點的雙親T _data;int _bf;                  // 該節點的平衡因子AVLTreeNode(const T& data): _left(nullptr), _right(nullptr), _parent(nullptr), _data(data), _bf(0){}
};
template<class T>
class AVLTree
{typedef AVLTreeNode<T> Node;
public:bool insert(const T& data){if (_root == nullptr){_root = new Node(data);return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_data < data){parent = cur;cur = cur->_right;}else if (cur->_data > data){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(data);if (parent->_data > data){parent->_left = cur;}else{parent->_right = cur;}while (parent){//左邊++if (cur == parent->_left){parent->_bf--;}//右邊--else{parent->_bf++;}//parent的平衡因子等于0，插入成功if (parent->_bf == 0){break;}//parent的平衡因子等于1或者-1，繼續向上更新else if (parent->_bf == 1 || parent->_bf == -1){cur = parent;parent = parent->_parent;}else if (parent->_bf == 2 || parent->_bf == -2){//需要進行旋轉if (parent->_bf == 2 && cur->_bf == 1){RotateL(parent);}else if (parent->_bf == 2 && cur->_bf == -1){RotateRL(parent);}else if (parent->_bf == -2 && cur->_bf == -1){RotateR(parent);}else if (parent->_bf == -2 && cur->_bf == 1){RotateLR(parent);}break;}else{assert(false);}}return true;}void RotateR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;parent->_left = subLR;//防止sublr為空if(subLR)subLR->_parent = parent;//記錄祖父位置Node* pparent = parent->_parent;subL->_right = parent;parent->_parent = subL;//如果父親是根節點if (parent == _root){_root = subL;subL->_parent = nullptr;}//parent不是根節點，那么祖父就會成為subl的parentelse{if (pparent->_left == parent){pparent->_left = subL;subL->_parent = pparent;}else{pparent->_right = subL;subL->_parent = pparent;}}//旋轉后parent和subl的 平衡因子都會更新為0parent->_bf = subL->_bf = 0;}void RotateL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;subR->_left = parent;Node* pparent = parent->_parent;if (subRL)subRL->_parent = parent;if (_root == parent){_root = subR;subR->_parent == nullptr;}else{if (pparent->_left == parent){pparent->_left = subR;subR->_parent = pparent;}else{pparent->_right = subR;subR->_parent = pparent;}}parent->_bf = subR->_bf = 0;}void RotateLR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;RotateL(parent->_left);RotateR(parent);int bf = subLR->_bf;//sublr就是新增節點if (bf == 0){parent->_bf = 0;subL->_bf = 0;subLR->_bf = 0;}//sublr左子樹新增節點else if (bf == -1){parent->_bf = 1;subL->_bf = 0;subLR->_bf = 0;}//sublr右子樹新增節點else if (bf == 1){parent->_bf = 0;subL->_bf = -1;subLR->_bf = 0;}else{assert(false);}}void RotateRL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;int bf = subRL->_bf;RotateR(parent->_right);RotateL(parent);//subrl這個點為新增點if (bf == 0){parent->_bf = subR->_bf = subRL->_bf = 0;}//subrl的左子樹新增else if (bf == -1){parent->_bf = 0;subRL->_bf = 0;subR->_bf = 1;}//subrl的右子樹新增else if (bf == 1){parent->_bf = -1;subRL->_bf = 0;subR->_bf = 0;}else{assert(false);}}int Height(Node* root){if (root == nullptr){return 0;}int leftheight = Height(root->_left);int rightheight = Height(root->_right);return leftheight > rightheight ? leftheight + 1 : rightheight + 1;}bool isbalance(){return _isbalance(_root);}bool _isbalance(Node* root){if (root == nullptr)return true;int leftheight = Height(root->_left);int rightheight = Height(root->_right);if (rightheight - leftheight != root->_bf){cout << root->_data << "平衡因子異常" << endl;return false;}return abs(rightheight - leftheight) < 2&& _isbalance(root->_left)&& _isbalance(root->_right);}void inorder(){_inorder(_root);cout << endl;}void _inorder(Node* root){if (root == nullptr){return;}_inorder(root->_left);cout << root->_data << " ";_inorder(root->_right);}private:Node* _root=nullptr;
};

好了，今天的分享到這里就結束了，感謝大家的支持！