---

LeNet-5（詳解）—— 從原理到 PyTorch 實現（含訓練示例）

簡介

LeNet-5 是 Yann LeCun 在 1998 年提出的一種經典卷積神經網絡（CNN），最早用于 手寫數字識別（MNIST 數據集）。它是深度學習的奠基網絡之一，對后續的 AlexNet、VGG、ResNet 等深度網絡有重要啟發。
論文：Gradient-based learning appl ied to document re cognition
中文可參考：論文
👉 本文目標：通過 逐層解析 LeNet-5 的思想，并在 PyTorch 中實現與訓練，讓你從 理論 → 實踐 → 實驗擴展 全面理解這一經典網絡。

---

LeNet-5 的核心思想

1. 局部感受野（Local Receptive Field）
   每個神經元只連接輸入圖像的一小塊區域，減少計算量并提取局部特征。

2. 權值共享（Weight Sharing）
   卷積層使用相同的卷積核（Filter）在整張圖像上滑動，極大減少參數數量。

3. 下采樣（Subsampling / Pooling）
   使用平均池化降低特征圖尺寸，保留關鍵信息，減少過擬合。

---

LeNet-5 逐層結構詳解

輸入為 32×32 灰度圖像（MNIST 原本是 28×28，論文中補 0 填充到 32×32）。一共七層，3個卷積層，2個池化層，2個全連接層

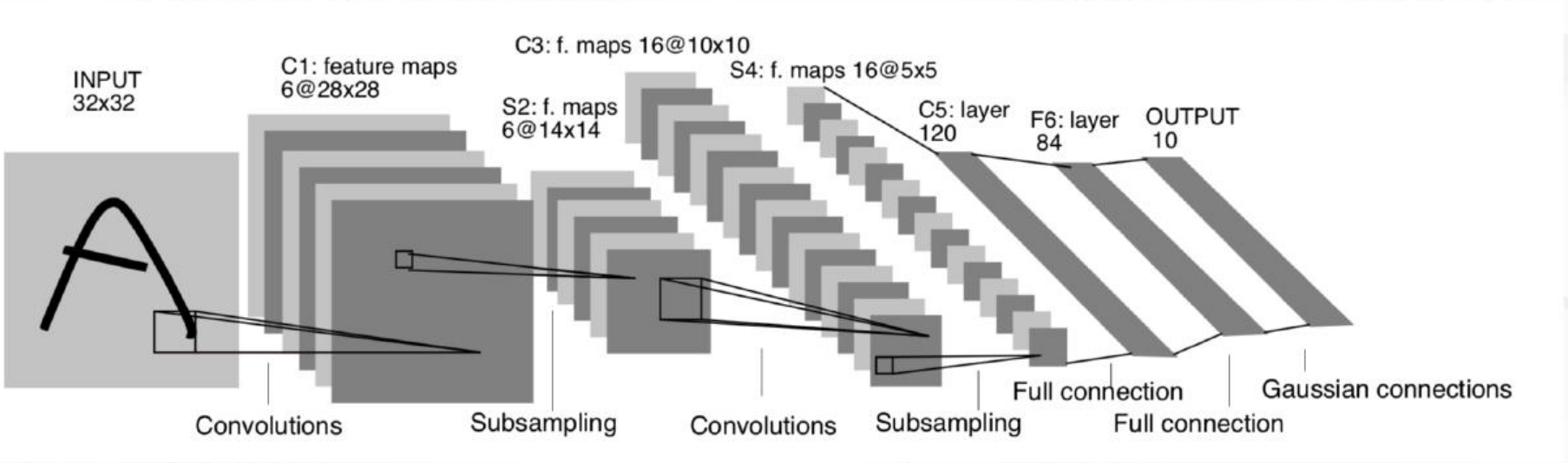
層級	類型	輸入尺寸	核心操作	輸出尺寸	參數量
輸入層	Image	32×32×1	-	32×32×1	0
C1	卷積層	32×32×1	6 個 5×5 卷積核，stride=1	28×28×6	156
S2	池化層	28×28×6	6 個 2×2 平均池化，stride=2	14×14×6	12
C3	卷積層	14×14×6	16 個 5×5 卷積核（部分連接）	10×10×16	≈1516
S4	池化層	10×10×16	16 個 2×2 平均池化，stride=2	5×5×16	32
C5	卷積層	5×5×16	120 個 5×5 卷積核（全連接方式）	1×1×120	48120
F6	全連接	120	全連接到 84 個神經元	84	10164
輸出層	Softmax	84	全連接到 10 類	10	850

---

逐層計算舉例

卷積與池化的計算公式：

• 卷積層公式：

  $$O=\frac{W?F+2P}{S}+1$$

  其中：

  • $W$：輸入特征圖大小
  • $F$：卷積核大小
  • $P$：Padding
  • $S$：步長 (stride)
  • $O$：輸出特征圖大小

• 池化層公式：同卷積公式，只是用池化窗口替換卷積核。

---

📌 輸入層

輸入：32×32×1（單通道灰度圖）

---

📌 C1 卷積層

• 輸入：32×32×1

• 卷積核：6 個 5×5，stride=1，padding=0

• 計算：

  $$O=\frac{32?5+0}{1}+1=28$$

• 輸出：28×28×6

---

📌 S2 池化層

• 輸入：28×28×6

• 池化窗口：2×2，stride=2

• 計算：

  $$O=\frac{28?2}{2}+1=14$$

• 輸出：14×14×6

---

📌 C3 卷積層

• 輸入：14×14×6

• 卷積核：16 個 5×5，stride=1，padding=0（部分連接）

• 計算：

  $$O=\frac{14?5}{1}+1=10$$

• 輸出：10×10×16

---

📌 S4 池化層

• 輸入：10×10×16

• 池化窗口：2×2，stride=2

• 計算：

  $$O=\frac{10?2}{2}+1=5$$

• 輸出：5×5×16

---

📌 C5 卷積層

• 輸入：5×5×16

• 卷積核：120 個 5×5（全連接形式）

• 計算：

  $$O=\frac{5?5}{1}+1=1$$

• 輸出：1×1×120

---

📌 F6 全連接層

• 輸入：120
• 輸出：84

---

📌 輸出層

• 輸入：84
• 輸出：10（分類類別：0~9）

---

關鍵設計點解析

1. C3 的部分連接

   • 并非所有 16 個卷積核都連接前一層的 6 個通道，而是選擇部分組合，減少參數。
   • 這是因為早期計算能力有限，同時也有助于增加特征多樣性。

2. S 層的帶學習系數平均池化

   • 與現代的 MaxPool 不同，LeNet-5 的平均池化包含一個可訓練的縮放系數 + 偏置。

   • 即：

     $$y=a?\text{avg}(x)+b$$

3. 激活函數 tanh

   • LeNet-5 使用 tanh / sigmoid 激活，而不是現代 CNN 常用的 ReLU。
   • 這導致梯度可能更容易消失，但在小規模網絡上問題不大。

---

PyTorch 實現 LeNet-5

import torch
import torch.nn as nn
import torch.nn.functional as Fclass LeNet5(nn.Module):def __init__(self, num_classes=10):super(LeNet5, self).__init__()# C1: 卷積層 1self.conv1 = nn.Conv2d(1, 6, kernel_size=5, stride=1, padding=0)# S2: 平均池化self.pool1 = nn.AvgPool2d(kernel_size=2, stride=2)# C3: 卷積層 2self.conv2 = nn.Conv2d(6, 16, kernel_size=5, stride=1, padding=0)# S4: 平均池化self.pool2 = nn.AvgPool2d(kernel_size=2, stride=2)# C5: 卷積層 3self.conv3 = nn.Conv2d(16, 120, kernel_size=5, stride=1, padding=0)# F6: 全連接層self.fc1 = nn.Linear(120, 84)# 輸出層self.fc2 = nn.Linear(84, num_classes)def forward(self, x):x = torch.tanh(self.conv1(x))   # C1x = self.pool1(x)               # S2x = torch.tanh(self.conv2(x))   # C3x = self.pool2(x)               # S4x = torch.tanh(self.conv3(x))   # C5x = x.view(x.size(0), -1)       # 展平x = torch.tanh(self.fc1(x))     # F6x = self.fc2(x)                 # 輸出層return x

---

訓練與評估

import torch.optim as optim
from torchvision import datasets, transforms# 數據準備（MNIST）
transform = transforms.Compose([transforms.Pad(2),   # MNIST 28x28 → 32x32transforms.ToTensor()
])
train_dataset = datasets.MNIST(root="./data", train=True, download=True, transform=transform)
test_dataset = datasets.MNIST(root="./data", train=False, download=True, transform=transform)train_loader = torch.utils.data.DataLoader(train_dataset, batch_size=64, shuffle=True)
test_loader = torch.utils.data.DataLoader(test_dataset, batch_size=1000, shuffle=False)# 模型、優化器、損失函數
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
model = LeNet5().to(device)
optimizer = optim.Adam(model.parameters(), lr=0.001)
criterion = nn.CrossEntropyLoss()# 訓練
for epoch in range(5):model.train()for data, target in train_loader:data, target = data.to(device), target.to(device)optimizer.zero_grad()output = model(data)loss = criterion(output, target)loss.backward()optimizer.step()print(f"Epoch {epoch+1}, Loss: {loss.item():.4f}")# 測試
model.eval()
correct = 0
with torch.no_grad():for data, target in test_loader:data, target = data.to(device), target.to(device)output = model(data)pred = output.argmax(dim=1)correct += pred.eq(target).sum().item()print("Test Accuracy: {:.2f}%".format(100. * correct / len(test_dataset)))

---

實驗擴展

我們可以對比 原版 LeNet-5 與現代改進版：

模型版本	激活函數	池化方式	歸一化	數據增強	測試準確率
原版 LeNet-5	tanh	AvgPool	無	無	~99.0%
改進版	ReLU	MaxPool	BatchNorm	隨機旋轉、平移	~99.3%

👉 結論：現代改進提升了訓練收斂速度與泛化性能。

---

總結

• LeNet-5 開創了 卷積、池化、全連接 的網絡結構范式。
• 逐層計算公式 能幫助我們直觀理解輸入輸出維度的變化。
• 其思想（局部感受野、權值共享、下采樣）成為后續 CNN 的基石。
• PyTorch 實現與 MNIST 訓練能直觀感受這一網絡的簡潔與高效。
• 現代改進（ReLU、MaxPool、BN、數據增強）進一步提升效果。

---

參考資料

1. Yann LeCun - LeNet-5 原始論文 (1998)
2. PyTorch 官方文檔：https://pytorch.org/docs/stable/nn.html
3. 深度學習經典模型講解 - CSDN 博客

---