把這場忘了。。官方也遲遲不發題解
比賽鏈接
出題人題解
A 小紅的字符串生成
思路:
枚舉四種字符串打印出來即可,為了防止重復可以用set先去一下重。
code:
#include <iostream>
#include <cstdio>
#include <cstring>
#include <set>
using namespace std;set<string> S;
string a,b;int main(){cin>>a>>b;S.insert(a);S.insert(b);S.insert(a+b);S.insert(b+a);cout<<S.size()<<endl;for(auto x:S)cout<<x<<endl;return 0;
}
B 小紅的非排列構造
思路:
如果它本身就不是一個排列,那么就不需要修改,如果是排列,我們就換一個不是排列中的數進去,那么它就一定不是排列了。
判定是否為排列的方法很多,我是先排序再去重,然后看一下兩頭的數是不是1和n就行了
code:
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
const int maxn=1e5+5;int n,a[maxn],cnt;int main(){cin>>n;for(int i=1;i<=n;i++)cin>>a[i];sort(a+1,a+n+1);cnt=unique(a+1,a+n+1)-a-1;if(cnt==n && a[1]==1 && a[n]==n)printf("1\n1 1000000");else printf("0");return 0;
}
C 小紅的數字拆解
思路:
看半天沒看懂,原來是切割數位啊😅
觀察一下不難發現,如果想要切割出來的數是個偶數,那么就需要個數為偶數,高位無所謂。而我們要盡可能切出來最多偶數,所以奇數一定和和它右邊遇到的第一個偶數進行結合。
切割方法找到了,現在問題變成了怎么存,怎么排序。一般想法是用string存,并用string內置的排序辦法。但是string排序默認是字典序排序而不是數字的先比數位。于是用結構體存一個string,并重載一下排序辦法就可以了。
code:
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <set>
#include <string>
using namespace std;string str,t;
struct Str{string s;Str(string x):s(x){};bool operator<(const Str x)const{if(s.size()==x.s.size())return s<x.s;return s.size()<x.s.size();}
};
multiset<Str> S;int main(){cin>>str;for(auto x:str){t+=x;if(~(x-'0')&1){S.insert(Str(t));t.clear();}}for(auto x:S)cout<<x.s<<endl;return 0;
}
D 小紅的陡峭值
思路:
手玩一會不難發現:中間的 0 0 0 都是沒用的。
如果中間的 0 0 0 都取兩邊其一的數,那么中間的 0 0 0 就可以看作沒有。而如果都不取,差值勢必大于1,直接就不滿足條件了。因此為了滿足條件,中間的 0 0 0 就只能取一邊的數,就相當于沒用。
現在有用的只有兩端的 0 0 0。我們用兩個 b o o l bool bool 變量 f 1 , f 2 f1,f2 f1,f2 記錄一下開頭和結尾有無 0 0 0,然后直接把原序列中所有的 0 0 0 全部去掉(或者直接先替換成一端的數)。問題變成了現在要如何填數?
發現需要求一下中間的數的陡峭值是多少,如果是 0 0 0,就需要兩端的 0 0 0 來補,如果是 1 1 1,就不需要兩端有 0 0 0,如果大于 1 1 1,直接無解。
code:
#include <iostream>
#include <cstdio>
using namespace std;
const int maxn=1e5+5;int n,a[maxn],cnt;int main(){cin>>n;if(n==1){printf("-1");return 0;}int flag=0;for(int i=1,t;i<=n;i++){cin>>a[i];if(a[i]==0){if(i==1)flag=1;else if(i==n)flag=2;//兩端有一端有就行了,所以用了一個變量a[i]=a[i-1];}}if(a[n]==0)a[n]=5;for(int i=n;i>=1;i--)if(a[i]==0)a[i]=a[i+1];int tot=0;for(int i=2;i<=n;i++)tot+=abs(a[i]-a[i-1]);if(tot==0 && flag){if(flag==1)a[1]=(a[2]==1)?2:a[2]-1;else if(flag==2)a[n]=(a[n-1]==1)?2:a[n-1]-1;for(int i=1;i<=n;i++)printf("%d ",a[i]);}else if(tot==1){for(int i=1;i<=n;i++)printf("%d ",a[i]);}else printf("-1");return 0;
}
E 小紅的樹形 dp
思路:
一開始的思路是:把一個點欽定為根節點,那么每個點的深度就確定了,如果某個點的值確定,那么對應奇數和偶數深度的點就確定了,然后巴拉巴拉。
不過不用那么麻煩,因為一個點確定了,其他點就隨之確定了,因此我們直接遍歷一下有沒有d或p,如果有,就以它為根節點開始往下填數,如果出現了沖突的點就無解。如果沒有d或p,就隨便填了。
code:
#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
const int maxn=1e5+5;int n;
string color;int head[maxn],cnt;
struct edge{int v,nxt;
}e[maxn<<1];
void add(int u,int v){e[++cnt].v=v;e[cnt].nxt=head[u];head[u]=cnt;
}void dfs(int u,int rt){for(int i=head[u],v;i;i=e[i].nxt){v=e[i].v;if(v==rt)continue;if(color[v]==color[u]){printf("-1");exit(0);}color[v]=(color[u]=='d')?'p':'d';dfs(v,u);}
}int main(){cin>>n>>color;color=" "+color;for(int i=1,u,v;i<n;i++){cin>>u>>v;add(u,v);add(v,u);}if(color.find_first_of("dp",1)!=string::npos)dfs(color.find_first_of("dp",1),-1);else {color[1]='d';dfs(1,-1);}cout<<color.substr(1);return 0;
}
F 小紅的矩陣構造
思路:
就是很固定的構造方式,官方講解講的已經很明白了,在視頻一小時九分那里。大概就是這個樣子:
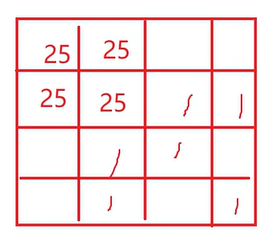
注意 n , m ≥ 4 n,m\ge 4 n,m≥4 還 x x x 是偶數。
code:
#include <iostream>
#include <cstdio>
using namespace std;int n,m,x;
int a[5][5];int main(){cin>>n>>m>>x;if(x==2)cout<<-1<<endl;else if(x%4==0){a[1][1]=a[1][2]=a[2][1]=a[2][2]=x/4;for(int i=1;i<=n;i++,puts(""))for(int j=1;j<=m;j++){if(i>4 || j>4)printf("0 ");else printf("%d ",a[i][j]);}}else {x-=6;a[1][1]=a[1][2]=a[2][1]=a[2][2]=x/4;a[3][2]=a[2][3]=a[3][3]=a[2][4]=a[4][2]=a[4][4]=1;for(int i=1;i<=n;i++,puts(""))for(int j=1;j<=m;j++){if(i>4 || j>4)printf("0 ");else printf("%d ",a[i][j]);}}return 0;
}
G 小紅的元素交換
思路:
用到了置換環這個小知識點。將排列打亂,然后給 a i → i a_i\rightarrow i ai?→i 連一條邊,連完之后就會出現多個環,只出現環的原因是:如果將每個位置看作一個點,每個點都只有一個入度和一個出度。而且環上每個位置上的數的正確位置都是它指向的下一個位置(廢話),也就是環上每個位置的數都只偏移了一位。
根據這個思路,可以把問題轉化為,多個置換環怎么把數歸位。假設環長為 a a a,發現如果環中兩種顏色都存在,那么它可以通過交換 a ? 1 a-1 a?1 次把所有數歸位。
歸位方法是:環上每一段連續的白色或黑色的最后一個標記一下,都先不動,然后從中隨便取一個開始向后給路上的每個點進行歸位,然后遇到下一個被標記的點,讓它接著向下交換,換一遍后剩下的就是黑白黑白顏色交替的顏色沒有歸位了,再隨便找一個,把它和在它的正確位置上的點交換位置(因為是黑白交替,它下一個位置的點一定和它顏色不同,所以一定是可以交換的),然后換出來的點以此類推和正確位置上的點交換,最后就能換好,因為每次交換都會有一個點被放入正確位置,而最后一次交換兩個點會同時歸位,所以一共需要 a ? 1 a-1 a?1 次交換。
如果是純色的環,就需要在別處借一個異色過來,然后再還回去,這就需要 a + 1 a+1 a+1 次交換。
但是如果有兩個不同純色的環,它們可以先交換其中一個點,兩邊都排好序后再換回來,這樣兩邊都只需要 a a a 次交換就可以了。
所以這個題我們需要統計每個環是同色還是異色,如果是異色就加 環長 ? 1 環長-1 環長?1,否則加 環長 + 1 環長+1 環長+1。再統計純黑和純白分別有幾個,最后再減去兩值小的*2就行了。啊嘞,好像不是黑色是紅色
code:
#include <iostream>
#include <cstdio>
#include <set>
#include <cstring>
#include <vector>
using namespace std;
const int maxn=1e5+5;int n,a[maxn];
string color;int main(){cin>>n;for(int i=1;i<=n;i++)cin>>a[i];cin>>color;color=" "+color;int ans=0,w=0,r=0;vector<bool> vis(n+5,false);for(int i=1;i<=n;i++){int cnt=0;bool f1=false,f2=false;//有紅 有白 if(!vis[i]){vis[i]=true;cnt++;if(color[i]=='W')f1=true;else f2=true;for(int p=a[i];p!=i;p=a[p]){vis[p]=true;cnt++;if(color[p]=='W')f1=true;else f2=true;}if(cnt==1)continue;else if(f1 && f2)ans+=cnt-1;else {ans+=cnt+1;if(f1)w++;else r++;}}}if(ans==0)cout<<0<<endl;else if(color.find("W")==string::npos || color.find("R")==string::npos)cout<<-1<<endl;else cout<<ans-min(w,r)*2<<endl;return 0;
}
詳解輪廓)
)




)



 on null 異常報錯處理)
)


)




