題目描述

根據題目信息，我們可以整理出一些基本思路。

1. 首先我們需要想辦法遍歷每層數據 其中需要記錄二叉樹當前深度。
2. 遍歷的過程中進行判斷，不符合要求就返回false

基本就需要做到這兩大板塊就可以完成我們的任務了。重要的是這個過程如何實現：這里我們用到兩個常用方法：廣度優先搜索 （BFS）和 深度優先搜索（DFS）。下面初步解釋一下兩種算法：

廣度優先搜索（BFS）

廣度優先搜索是連通圖的一種遍歷算法，是很多重要圖算法的原型（比如Dijkstra最短路徑算法和Prim最小生成樹算法）。它是一種盲目搜索法，目的是展開并檢查圖中的所有節點，進而得到結果。
過程是十分暴力的，不考慮結果的具體位置，直接遍歷搜索所有節點，直到找到結果為止。基本過程是從根節點開始，沿著樹（圖）遍歷所有節點，訪問完所以節點后算法終止。常使用隊列（FIFO）輔助實現BFS算法。

深度優先算法（DFS）

深度優先算法是圖論的經典算法，是針對圖和樹的遍歷算法（比如前序遍歷，中序遍歷，后序遍歷）。利用深度優先算法可以產生目標圖的對應拓撲排序表，進而方便的解決問題（如最大路徑算法）。
其過程簡單來說是對一個可能分支進行處理到不能再進行處理為止。如果是死路就返回，返回圖中遇見未探索的分支就進行進行處理，直到達到要求。一般使用堆或棧來輔助實現DFS算法。

思路一（BFS）

根據上面的介紹我們可以通過隊列來輔助我們進行遍歷所有樹。
具體分為兩個循環嵌套：

1. 首先外圍while 保證訪問所有節點，并記錄深度。
2. 內層for循環 負責處理該層所有節點，并將下一層節點存入隊列中。

接下來是一些細節：

1. leve記錄層數 （注意從0開始）
2. prev 記錄上一個節點數
3. value記錄當前節點數
4. prev 處理完每個節點后 需要迭代。
5. 每層處理結束后 level++
   這兩個循環是算法的核心部分， 保證了遍歷所有節點.
   來看代碼實現（選擇使用C++ 比較方便）

class Solution {
public:bool isEvenOddTree(TreeNode* root) {//建立隊列queue<TreeNode*> qu;//先入根節點qu.push(root);//設置層數int level = 0;//開始遍歷 隊列全為空就結束while(!qu.empty()){//prev 為前一個節點值 這里進行初始化//偶數下標 層上的所有節點的值都是 奇整數，從左到右按順序嚴格遞增//所以 prev設置為最小值//奇數下標 層上的所有節點的值都是 偶整數，從左到右按順序嚴格遞減//所以 prev設置為最大值int prev = level % 2 == 0 ? INT_MIN : INT_MAX;//獲取當前層節點個數int size = qu.size();//進入該層循環for(int i = 0 ; i < size ;i++){//出隊列 得到節點TreeNode* node = qu.front();qu.pop();//獲取當前節點值int value = node->val;//節點值 與 該層數奇偶不符 返回 falseif(value % 2 == level % 2) return false;//偶數下標層 必須滿足嚴格遞增 通過當前值與上一個節點值進行判斷if(level % 2 == 0 && value <= prev) return false;//奇數下標層 必須滿足嚴格遞減 通過當前值與上一個節點值進行判斷if(level % 2 == 1 && value >= prev) return false;//進行入隊列處理if(node->left) qu.push(node->left);if(node->right) qu.push(node->right);//該節點結束 先前節點值迭代prev = value;}//層數增加level++;}//全部滿足條件 返回真即可return true;}
};

來看效果：

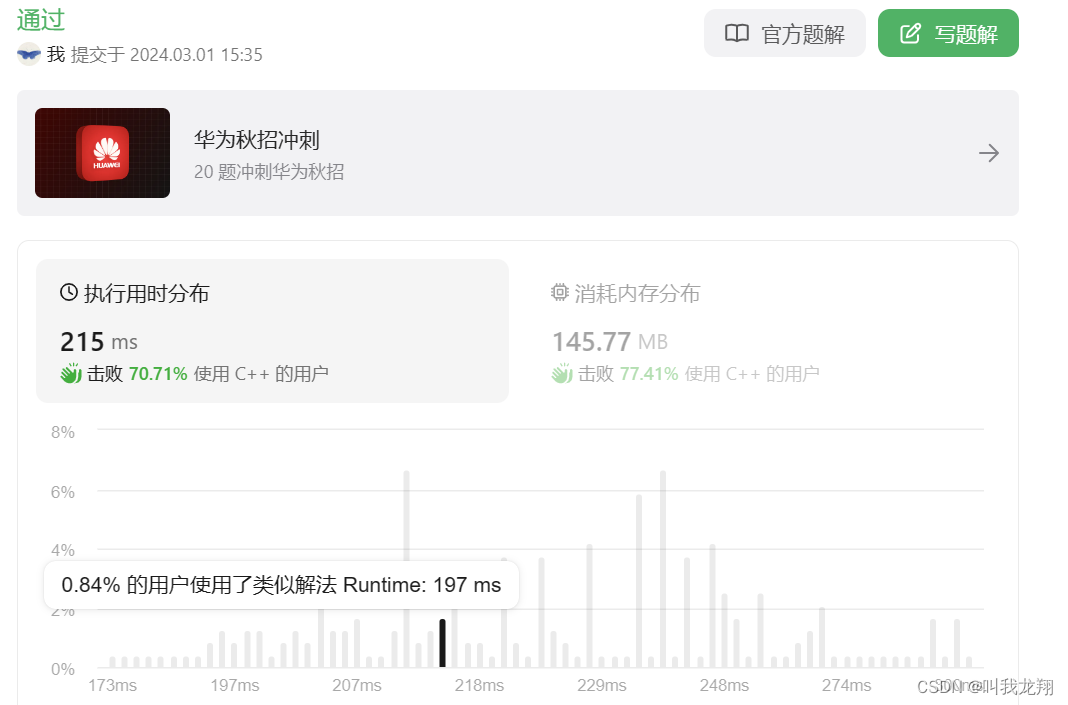
過啦！！！ 大聲歡呼！！！

思路二（DFS）

該思路使用遞歸，所以有點不太好理解，動態規劃好DFS 的混合運算了屬于。
我們寫出的dfs函數主要完成以下工作：
bool dfs(TreeNode* root,int p)

1. root 為當前節點 p 為層數 dp[ p ]儲存該層最新的數值
2. 首先判斷是否滿足基本條件：
   偶數下標 層上的所有節點的值都是 奇 整數，從左到右按順序 嚴格遞增
   奇數下標 層上的所有節點的值都是 偶 整數，從左到右按順序 嚴格遞減
   判斷遞增遞減是通過 當前節點值與dp[ p ]的值進行比較
   滿足條件就更新dp[ p ] 值
3. 然后進行下一層的判斷
4. 直到處理完所有數據。

//設置常量 方便使用
const int N = 1e5 + 7;
const int MAX = 0x3f3f3f3f;
class Solution {
public:// dp[]數組儲存上一個符合要求的值 int dp[N + 1];bool dfs(TreeNode* root,int p){//記錄當前節點值int value = root->val;//奇數下標層 必須滿足嚴格遞減 通過當前值與上一個節點值進行判斷if(p & 1){if(value & 1 || value >= dp[p]) return false;}//偶數下標層 必須滿足嚴格遞增 通過當前值與上一個節點值進行判斷else{if(!(value & 1) || value <= dp[p]) return false;}//滿足條件就更新數組值dp[p] = value;//繼續深入處理if(root->left && !dfs(root->left,p+1)) return false;if(root->right && !dfs(root->right,p+1)) return false;//符合要求 返回真return true;}bool isEvenOddTree(TreeNode* root) {for(int i = 0;i<N;i+=2) {dp[i] = 0;//偶數下標 需要遞增所以使用最小值0dp[i + 1] = MAX;//奇數下標 需要遞增所以使用最小值0}return dfs(root,0);}
};

來看效果：

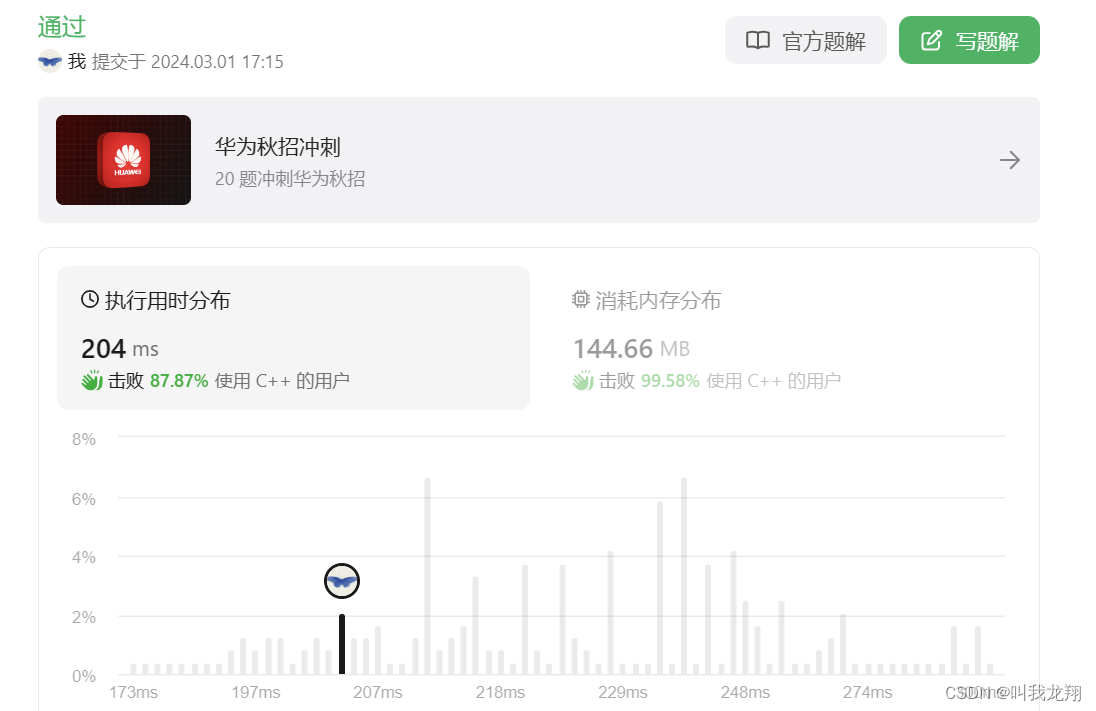
過啦！！！！！！！！！！！！！！！！！！！

這道題是我目前做過最難的題，雖然沒有一遍做出來，但是參考大佬的代碼，慢慢啃的感覺的真的很好。刷題繼續！！！！！！

Thanks?(･ω･)ﾉ謝謝閱讀！！！

下一篇文章見！！！