古人有云，物以類聚，在面臨信息爆炸問題的今天，對信息類別劃分的價值日益顯現，并逐步成為學者們的研究熱點。分類和聚類是數據挖掘的重要工具，是實現事物類別劃分的左右手，聚類又是分類一種特殊的方式。所謂聚類，淺顯的講就是將指定數據集中的個體（或對象）按照某種約定規則劃分成若干個類別（也稱簇、組），使得劃分在同一類中的個體間具有強的共性特征，而分在不同類中的個體間差異最大化。聚類作為一種無監督的機器學習過程，它是基于觀察的學習而不是基于實例的學習，所以事先無需確定分類的準則和先驗知識，所以和有監督的機器學習方法相比，聚類分析方法更具靈活性。通過聚類分析技術，可以在不受人的先驗知識的束縛和干擾的情況下完成對無標識的數據對象類別劃分，從而獲取數據集合中潛在信息。

隨著聚類算法研究的深入，聚類在自然科學和社會科學的各個領域都得到了廣泛的應用，例如，搜索引擎門戶網站使用聚類來實現信息的快速定位，提高搜索效率；金融機構通過聚類來挖掘客戶的資料信息，實現風險的最小化；生物學家通過對含有遺傳信息的基因聚類來發現種群間的異同等。

聚類經過近幾十年的發展，已經有上千種聚類算法被提出，在最近的十幾年的時間里，提出的具有代表性的聚類算法有譜聚類算法、粒子群算法和近鄰傳播算法等。在現有的眾多聚類方法中，K-means算法是使用最普遍最經典的聚類算法之一，算法實現簡單，執行效率高。然而，K-means算法是建立在凸球形的樣本空間上基于中心的聚類算法，其準則函數是基于梯度的，僅在緊湊的具有超球空間結構的樣本集上才能得到較好的聚類結果，當樣本集空間結構非凸時，算法就會陷入局部最優劃分的困境中。

譜聚類算法對數據的結構分布不做強的假設，在非凸結構的數據集上任然能夠得到較好的聚類結果，克服了以經典K-means算法為代表的的基于中心聚類算法的缺點。此外，譜聚類對誤差數據和噪聲的敏感性不強，具有較好的魯棒性。在許多實際應用問題中，譜聚類都能取得較好的聚類效果。在最近的十年里，譜聚類方法日益受到學者們的關注并取得了迅猛的發展，和現有的主要聚類方法相比，譜聚類方法的優點明顯：

（1）算法實現起來直觀、簡單、方便，算法的核心問題為權矩陣的特征值分解，是一個經典的代數運算；（2）聚類結果穩定，算法不存在局部最優解；（3）對數據集的空間結構形狀不做強的要求，可以產生高質量的聚類結果；（4）理論基礎堅實，可以從譜圖理論、矩陣擾動理論、圖上隨機游走理論等多個角度給出合理解釋。

基于此，提出一種基于隨機游走拉普拉斯算子的快速譜聚類方法，算法運行環境為MAYLAB R2018A，部分代碼如下：

% Fast Spectral Clustering based on RandomWalk Laplacian 
% Input:
%       - Z: the initial cross similarity matrix between data points and anchors
%       - c: the number of clusters
% Output:
%       - clustering: the cluster assignment for each point
% Requre:
% 		mySVD.m
% 		litekmeans.m
% Usage:
%       % X: d*n
%       [laKMM, laMM, AnchorGraph, Anchors, ~, ~, ~]= KMM(X', c, m,k) ;Dv=diag(1./sum(Z,1));
U = mySVD(Z+Z*Dv,c+1);
U(:,1) = [];
U=U./repmat(sqrt(sum(U.^2,2)),1,c);
clustering=litekmeans(U,c,'MaxIter',100,'Replicates',10);

出圖如下：

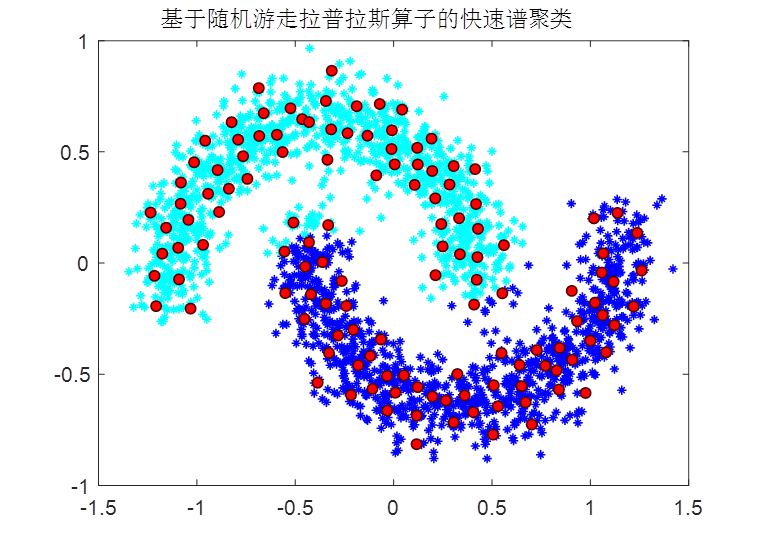
工學博士，擔任《Mechanical System and Signal Processing》審稿專家，擔任
《中國電機工程學報》優秀審稿專家，《控制與決策》，《系統工程與電子技術》，《電力系統保護與控制》，《宇航學報》等EI期刊審稿專家。

擅長領域：現代信號處理，機器學習，深度學習，數字孿生，時間序列分析，設備缺陷檢測、設備異常檢測、設備智能故障診斷與健康管理PHM等。