目錄
- 極值理論介紹
- GEV
- POT
- 代碼實現
極值理論介紹
在風險管理中,將事件分為高頻高損、高頻低損、低頻高損、低頻低損。其中低頻高損是一種非常棘手的損失事件,常出現在市場大跌、金融體系崩潰、金融危機以及自然災害等事件中。
由于很難給極端事件一個準確的定義,所以可觀測的歷史數據非常少。這種問題不僅僅出現在風險管理領域,在其他行業也很普遍。
極值理論(Extreme-value theory )是統計學的一種專門用于研究隨機變量分布的極端尾部行為。與一般的中心趨勢型統計方法不同,中心趨勢性統計方法核心是中心極限定理,但是極端值無法應用中心極限定理(中心極限定理假設樣本數量足夠大時服從正態分布)。
GEV
假設一個隨機損失變量X是獨立同分布的(iid)。從F(x)中抽取的一個樣本大小為n,且該樣本的最大值為M(如果n很大,我們可以把M看作一個極值)。根據Fisher-Tippett定理,當n變大時,極值(即Mn)的分布收斂到下面的廣義極值(GEV)分布
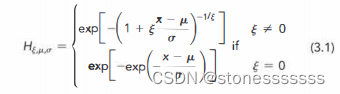
其中
μ \mu μ:極端值的平均數
σ \sigma σ:極端值的標準差
? \epsilon ?:形狀參數,描述極值分布的尾部形狀
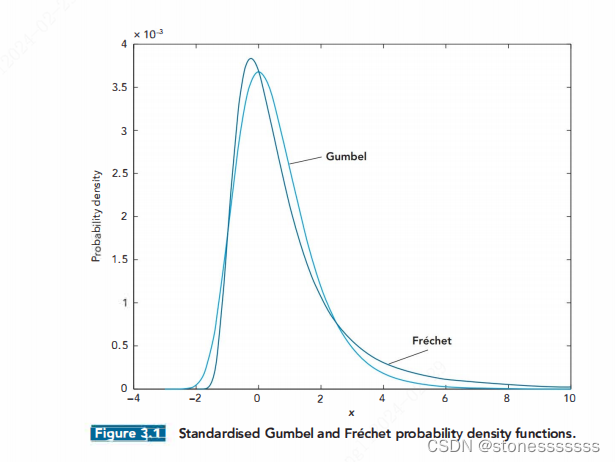
當 ? > 0 \epsilon>0 ?>0,服從Frechet分布,呈現出肥尾的特點。比如t分布,帕累托分布。
當 ? = 0 \epsilon=0 ?=0,服從Gumbel分布,呈現出指數型尾部,尾部相對瘦(light)。比如正態分布,對數正態分布。
當 ? < 0 \epsilon<0 ?<0,服從Weibull分布,呈現出比正態分布尾部更瘦的形態。該分布尤其不適用在金融實證中,由于金融數據一般呈現肥尾的特點。
POT
GEV在實際應用中可能會漏掉極值點,POT在此基礎上進行改良,先設定一個閾值(threshold),超過閾值的損失分布服從POT分布,這種方法比GEV方法需要更少的參數。
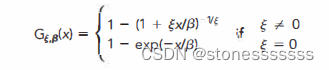
β \beta β:規模參數
? \epsilon ?:形狀參數,描述極值分布的尾部形狀
由此可推導VaR和ES的計算方法:
V a R = μ + β ? { [ n N u ( 1 ? α ) ? ? ] ? 1 } VaR=\mu+\frac{\beta}{\epsilon}\{[\frac{n}{N_{u}}(1-\alpha)^{-\epsilon}]-1\} VaR=μ+?β?{[Nu?n?(1?α)??]?1}
E S = V a R 1 ? ? + β ? ? μ 1 ? ? ES = \frac{VaR}{1-\epsilon}+\frac{\beta-\epsilon\mu}{1-\epsilon} ES=1??VaR?+1??β??μ?
代碼實現
from prettytable import PrettyTable
import numpy as np
import akshare as ak
from scipy.stats import genextreme as gev
from scipy.stats import genpareto as pot# 利用akshare讀取股票收益序列
stock = ak.stock_zh_a_hist(symbol='000001', period="daily", start_date="20071012", end_date='20081012', adjust="")
price = stock['收盤']# GEV
c, loc, scale = gev.fit(price[price < np.percentile(price, 5)])
confidence_level = 0.95
VaR_gev = gev.ppf(confidence_level, c, loc, scale)# POT
threshold = 17
choose = price[price < threshold]
c, beta, epsilon = pot.fit(choose)
n = float(len(price))
nu = float(len(choose))
VaR_POT = choose.mean() + beta/epsilon * ((n / nu * (confidence_level ** (-float(epsilon)))) - 1)# print
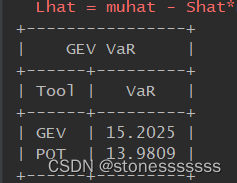
VaR = PrettyTable(['Tool', 'VaR'])
VaR.add_row(['GEV', round(VaR_gev, 4)])
VaR.add_row(['POT', round(VaR_POT, 4)])
print(VaR.get_string(title="GEV VaR"))
輸出結果:


)



數據預處理)



)

(DNA序列修正、無盡的石頭))
-個人筆記)





