一般情況下,機械振動信號或地震信號是非平穩的。而傳統傅立葉變換只能應用于平穩信號分析,故不適用于非平穩信號。所以,我們需要采用時頻分析方法。時頻分析方法能達到同時在時間域和頻率域對信號進行分析的目的,得到信號在不同時刻的部分頻譜特性。在信號領域中時頻分析是一種熱門方法,上世紀以來,時頻分析得到較快發展,各種時頻分析方法在各方面得到廣泛應用。
1946年提出的Gabor變換原理是應用基函數對信號進行分解,窗函數的時間域移動和頻率域移動產生基函數。1947年R.K.Potter等人首次提出了短時傅里葉變換,基本思想為:假定非平穩信號在窗函數內是平穩的。首先計算每個時窗內的傅里葉變換,然后在時間軸移動窗函數,得到信號隨時間變化的頻譜。由于窗函數是固定不變,因此無法在時間域和頻率域同時得到較高的分辨率。但是計算方法簡單,故應用廣泛。1948年,Wigner‐Ville分布由J.Ville應用于信號處理領域,Wigner‐Ville分布是二次型時頻分布,能量聚集效果較好,然而由于存在交叉項,故其應用被限制。Cohen在1966年給出了Cohen類時頻分布表達式,不同分布可由不同核函數得到。根據時頻分布特性,得到新的分布。對核函數施加制約條件便得到理想的時頻分布特性。法國地球物理學家Morlet在1982年首次將時頻分析方法應用于地震信號領域,并和Grossman提出小波變換。小波變換為一種多尺度分析方法。該方法可反映局部信息,但是計算復雜,效率太低,花費時間較長。1996年,Stockwell等首次提出S變換,S變換中窗函數隨頻率變化。頻率增加,則窗函數變窄,故低頻分量對應較高頻率分辨率,高頻對應較高時間分辨率。但其窗函數變化趨勢是固定,故其應用受到限制。2003年,Pinnegar等提出了廣義S變換概念,廣義S變換是可調節窗口的。2003年,高靜懷引入廣義S變換,不同的基本小波即對于不同的廣義S變換。2008年,陳學華在S變換的高斯窗上引入兩個參數λ和p,提出了另一種廣義S變換。廣義S變換通過引入兩個參數來調節窗函數,具有更高的適應性。2009年,Sinha首次提出了時頻連續小波變換。與小波變換相比,此方法消除了能量交疊現象。
為了進一步提高信號的視頻分辨率,提出一種新穎的類脈沖信號的高分辨率時頻分析方法,該方法針對同步壓縮變換因應用狄拉克函數僅能處理弱頻變信號方面的局限性,采用迭代法解決了模糊時頻分析問題,給出了3個模擬信號的例子。壓縮包=代碼+模擬信號+參考文獻。算法可遷移至金融時間序列,地震信號,機械振動信號,語音信號,聲信號,生理信號(ECG,EEG,EMG)等一維時間序列信號。
clc; clear; close all;
%Parameters
n = 1024;
fs = 1024;
t = 1/fs : 1/fs : 1;
Sig=sin(2*pi*(75*t+30*t.^3))+sin(2*pi*(340*t-2*exp(-2*(t-0.2)).*sin(14*pi*(t-0.2))));
f=(fs/2)/(n/2):(fs/2)/(n/2):(fs/2);
num = 3;
% Test Signal
y=Sig;
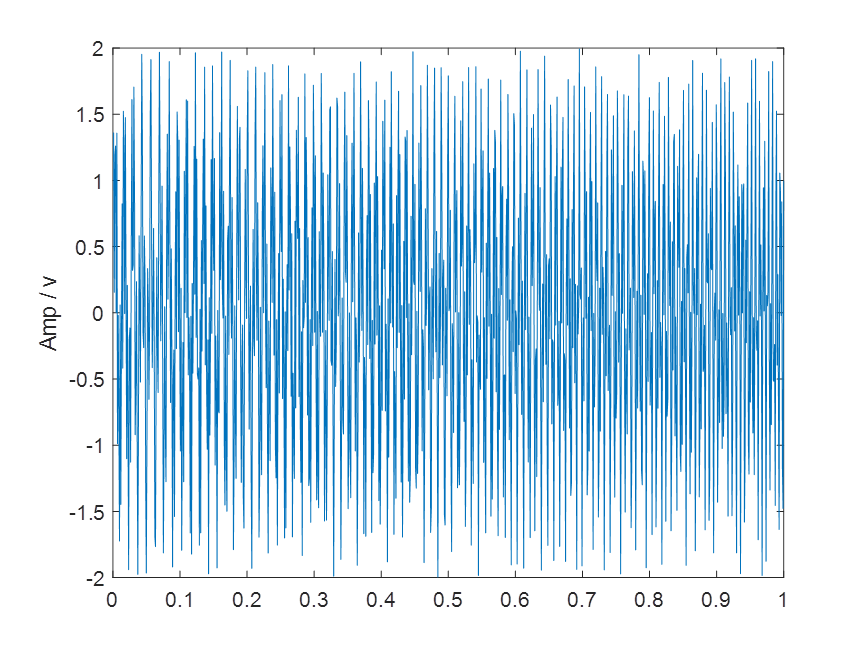
%original time domain waveform
figure;
plot(t,y)
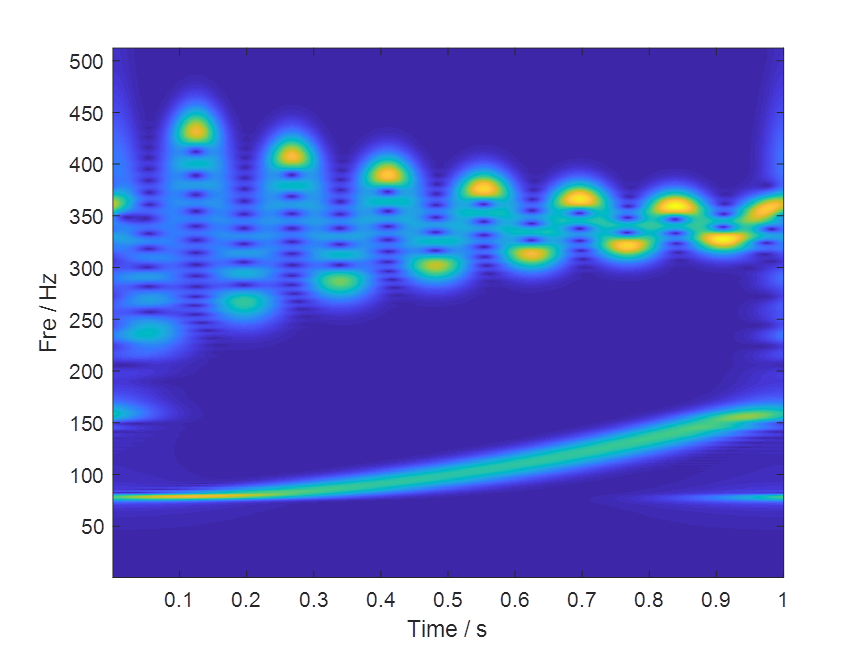
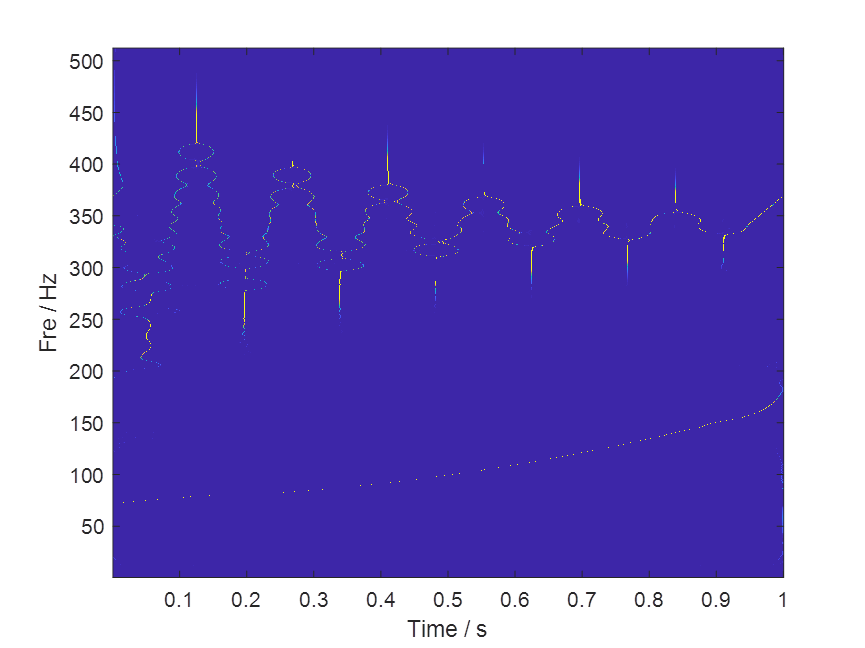
ylabel('Amp / v')部分出圖如下:
工學博士,擔任《Mechanical System and Signal Processing》審稿專家,擔任
《中國電機工程學報》優秀審稿專家,《控制與決策》,《系統工程與電子技術》,《電力系統保護與控制》,《宇航學報》等EI期刊審稿專家。
擅長領域:現代信號處理,機器學習,深度學習,數字孿生,時間序列分析,設備缺陷檢測、設備異常檢測、設備智能故障診斷與健康管理PHM等。




)














