【LetMeFly】2581.統計可能的樹根數目：換根DP(樹形DP)

力扣題目鏈接：https://leetcode.cn/problems/count-number-of-possible-root-nodes/

Alice 有一棵 n 個節點的樹，節點編號為 0 到 n - 1 。樹用一個長度為 n - 1 的二維整數數組 edges 表示，其中 edges[i] = [ai, bi] ，表示樹中節點 ai 和 bi 之間有一條邊。

Alice 想要 Bob 找到這棵樹的根。她允許 Bob 對這棵樹進行若干次 猜測 。每一次猜測，Bob 做如下事情：

• 選擇兩個 不相等?的整數?u 和?v?，且樹中必須存在邊?[u, v]?。
• Bob 猜測樹中?u?是?v?的 父節點?。

Bob 的猜測用二維整數數組?guesses 表示，其中?guesses[j] = [uj, vj]?表示 Bob 猜?uj 是?vj?的父節點。

Alice 非常懶，她不想逐個回答?Bob 的猜測，只告訴 Bob 這些猜測里面 至少?有?k?個猜測的結果為?true?。

給你二維整數數組 edges?，Bob 的所有猜測和整數?k?，請你返回可能成為樹根的?節點數目?。如果沒有這樣的樹，則返回 0。

?

示例 1：

輸入：edges = [[0,1],[1,2],[1,3],[4,2]], guesses = [[1,3],[0,1],[1,0],[2,4]], k = 3
輸出：3
解釋：
根為節點 0 ，正確的猜測為 [1,3], [0,1], [2,4]
根為節點 1 ，正確的猜測為 [1,3], [1,0], [2,4]
根為節點 2 ，正確的猜測為 [1,3], [1,0], [2,4]
根為節點 3 ，正確的猜測為 [1,0], [2,4]
根為節點 4 ，正確的猜測為 [1,3], [1,0]
節點 0 ，1 或 2 為根時，可以得到 3 個正確的猜測。

示例 2：

輸入：edges = [[0,1],[1,2],[2,3],[3,4]], guesses = [[1,0],[3,4],[2,1],[3,2]], k = 1
輸出：5
解釋：
根為節點 0 ，正確的猜測為 [3,4]
根為節點 1 ，正確的猜測為 [1,0], [3,4]
根為節點 2 ，正確的猜測為 [1,0], [2,1], [3,4]
根為節點 3 ，正確的猜測為 [1,0], [2,1], [3,2], [3,4]
根為節點 4 ，正確的猜測為 [1,0], [2,1], [3,2]
任何節點為根，都至少有 1 個正確的猜測。

?

提示：

• edges.length == n - 1
• 2 <= n <= 105
• 1 <= guesses.length <= 105
• 0 <= ai, bi, uj, vj <= n - 1
• ai != bi
• uj != vj
• edges?表示一棵有效的樹。
• guesses[j]?是樹中的一條邊。
• guesses?是唯一的。
• 0 <= k <= guesses.length

方法一：換根DP(樹形DP)

首先我們可以把所有的猜想都存入哈希表中，以便對于某條邊，能快速知道其是否有被猜過。

由于節點范圍是$10^5$，因此可以將$父節點\times 10^6+子節點$作為哈希表的鍵值。（注意可能會超32位整數）

假如只問“0”為根的話猜中次數是否$\ge k$，那么我們只需要從$0$開始對樹進行深度優先搜索：

搜索過程中統計邊被猜中的次數（借助哈希表可以在$O(1)$時間內完成一次查詢），搜索結束后判斷是否$\ge k$。

現在要問“各個節點”為根的話猜中次數。怎么辦？在原有結果的基礎上再DP一次即可：

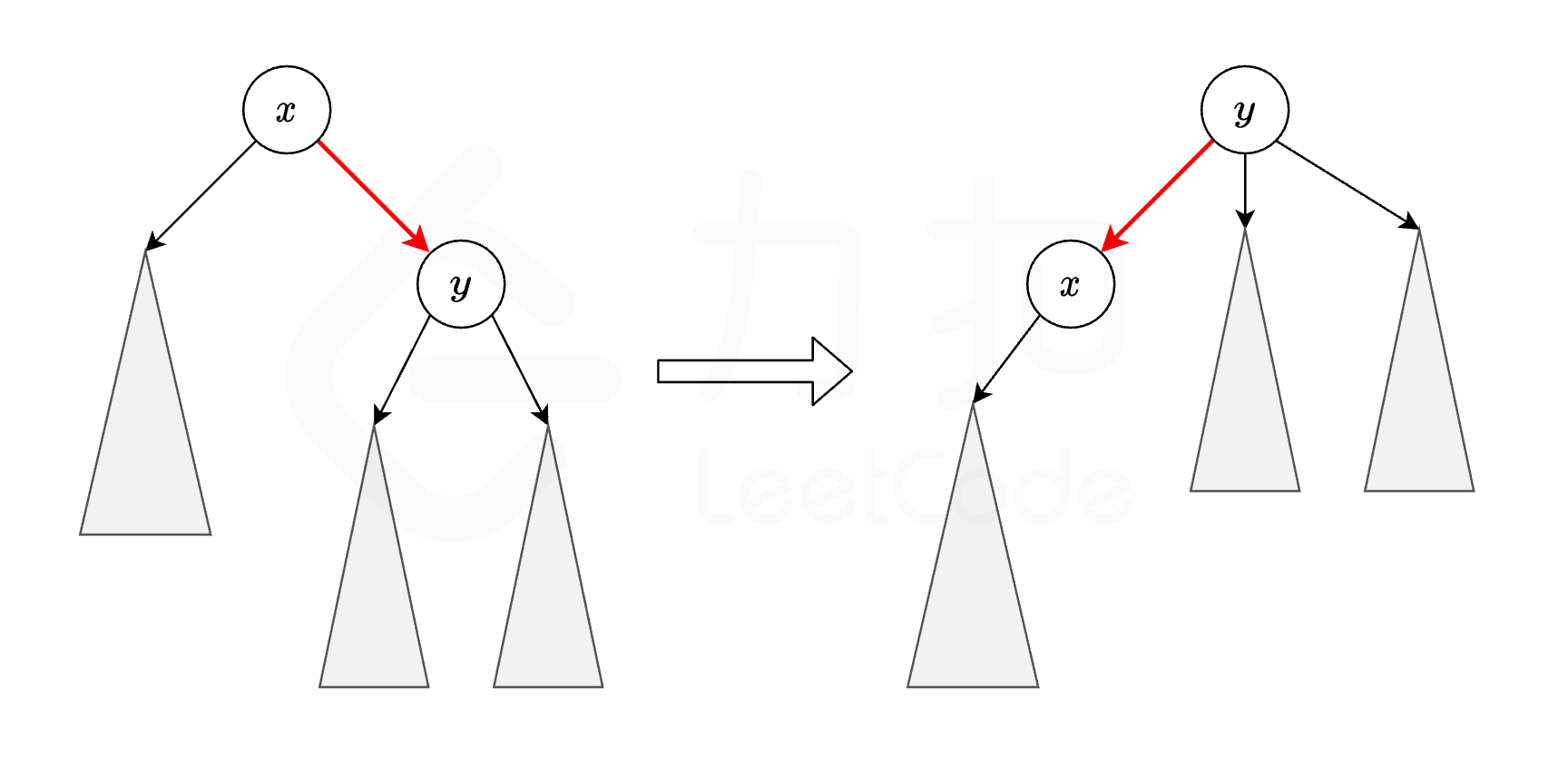
假設在現有的基礎上，x是y的父節點。此時有cnt個猜中的邊。若把y變成x的父節點呢？

變化的只有x與y之間的一條邊。

若有猜(x, y)，則猜中次數$cnt?1$；若有猜(y, x)，則猜中次數$cnt+1$。

DP過程中（其實就是沿邊走的過程）不斷將父子關系對調，并統計$cnt\ge k$的個數即為答案。

• 時間復雜度$O(N+M)$，其中$N$是樹的節點個數，$M=len(guesses)$
• 空間復雜度$O(N+M)$

AC代碼

C++

typedef long long ll;
class Solution {
private:int cnt;  // 以0為根時答對的數目int ans;int k;vector<vector<int>> graph;unordered_set<ll> se;void dfs(int thisNode, int lastNode=-1) {for (int nextNode : graph[thisNode]) {if (nextNode == lastNode) {continue;}if (se.count((ll)thisNode * 1000000 + nextNode)) {cnt++;}dfs(nextNode, thisNode);}}void change(int thisNode, int lastNode, int cnt) {int cnt_bak = cnt;for (int nextNode : graph[thisNode]) {if (nextNode == lastNode) {continue;}if (se.count((ll)thisNode * 1000000 + nextNode)) {cnt--;}if (se.count((ll)nextNode * 1000000 + thisNode)) {cnt++;}ans += cnt >= k;change(nextNode, thisNode, cnt);cnt = cnt_bak;}}
public:int rootCount(vector<vector<int>>& edges, vector<vector<int>>& guesses, int k) {graph.resize(edges.size() + 1);for (vector<int>& edge : edges) {graph[edge[0]].push_back(edge[1]);graph[edge[1]].push_back(edge[0]);}for (vector<int>& guess : guesses) {se.insert((ll)guess[0] * 1000000 + guess[1]);}cnt = 0;this->k = k;dfs(0);ans = cnt >= k;change(0, -1, cnt);return ans;}
};

Python

from typing import Listclass Solution:  # AC,100.00%,92.59%def dfs(self, thisNode: int, lastNode: int) -> None:for nextNode in self.graph[thisNode]:if nextNode == lastNode:continueif (thisNode * 1000000 + nextNode) in self.se:self.cnt += 1self.dfs(nextNode, thisNode)def change(self, thisNode: int, lastNode: int, cnt: int) -> None:cnt_bak = cntfor nextNode in self.graph[thisNode]:if nextNode == lastNode:continueif (thisNode * 1000000 + nextNode) in self.se:cnt -= 1if (nextNode * 1000000 + thisNode) in self.se:cnt += 1self.ans += cnt >= self.kself.change(nextNode, thisNode, cnt)cnt = cnt_bak            def rootCount(self, edges: List[List[int]], guesses: List[List[int]], k: int) -> int:self.graph = [[] for _ in range(len(edges) + 1)]for x, y in edges:self.graph[x].append(y)self.graph[y].append(x)self.se = set()for x, y in guesses:self.se.add(x * 1000000 + y)self.cnt = 0self.dfs(0, -1)self.k = kself.ans = 1 if self.cnt >= k else 0self.change(0, -1, self.cnt)return self.ans

同步發文于CSDN和我的個人博客，原創不易，轉載經作者同意后請附上原文鏈接哦~
Tisfy：https://letmefly.blog.csdn.net/article/details/136372137