論文閱讀/博弈論/拍賣：《Truthful Auction for Cooperative Communications》

摘要：

一方面，協作通信由于其在提升無線網絡容量方面的巨大潛力而日益受到關注。另一方面，協作通信技術的實際應用卻很少見，即使在一些對帶寬需求極高的應用場景中，系統設計者也并未采用協作通信技術來開發創新的網絡解決方案。協作通信從理論上能夠提高信道容量，但其廣泛應用面臨的主要障礙是缺乏激勵機制，促使參與節點愿意充當中繼節點。因此，在本文中，我們設計了一種名為TASC的拍賣方案，用于協作通信中的中繼服務交易。TASC在實現其他設計目標的同時，還保證了機制的真實性。我們通過理論分析證明了TASC具有真實性，并且時間復雜度為多項式級別。大量實驗表明，TASC能夠在不顯著降低性能的情況下實現多種經濟特性。

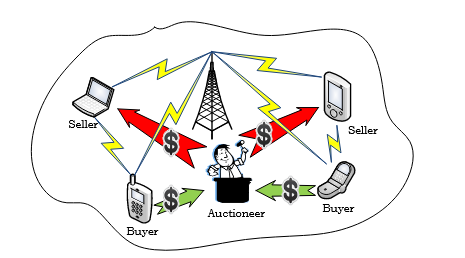
圖1：協作通信的拍賣過程。中繼節點（賣方）提供其中繼服務的價格，源節點（買方）競標這些服務以實現協作通信。基站（拍賣人）確定中標者及清算價格。

TASC

INTRODUCTION：
與3G/4G無線網絡相比，協作通信技術不需要額外的基礎設施，并且具有靈活性的優勢。然而，協作通信技術在實現信道容量提升潛力與廣泛應用之間面臨的主要障礙，是缺乏激勵機制來促使參與節點充當中繼節點。為什么一家手機運營商會愿意以犧牲自身資源為代價來中繼另一家運營商的流量呢？對此問題的一個答案是讓中繼節點能夠獲得相應的經濟回報。因此，需要在請求中繼服務的無線節點和提供中繼服務的節點之間建立一種交易機制。拍賣是最流行的交易形式之一[12]，因為它可以實現競爭性價格發現，以及公平高效的資源分配。

????????涉及買家和賣家的拍賣稱為雙向拍賣（double auction）。更具體地說，本文設計的雙向拍賣方案屬于單輪多物品雙向拍賣。在該拍賣方案中，如圖1所示，有n個買家對來自m個賣家的多個物品感興趣。

????????拍賣機制是交易市場中的一個關鍵方面，因為拍賣方案不僅直接定義了交易規則，還隱含地決定了參與代理的行為。具體而言，真實性（也稱為策略穩健性）是拍賣方案中最關鍵的特性。如果無論其他參與者采取何種策略，每個參與者的主導策略都是如實披露其真實的私有價值，則該拍賣方案即為真實性的。理論和實踐都表明，如果這一特性得不到保證，拍賣可能會受到市場操縱的影響，并產生非常糟糕的結果[11]。除了真實性之外，在設計拍賣方案時，以下特性也是理想的：1）個體理性：每個參與拍賣的代理都能期望獲得非負收益；2）預算平衡：拍賣方在拍賣結束后不應出現虧損；3）系統效率：所有代理估值之和達到最優，例如本文中總容量的最大化。遺憾的是，[16]中著名的結論表明，即使不考慮個體理性，任何雙側拍賣機制都無法同時實現真實性、預算平衡和系統效率。由于本研究的目標是激勵無線節點參與中繼服務，因此我們專注于設計滿足真實性、個體理性和預算平衡的方案。本文中，我們設計了一種用于協作通信的真實拍賣方案（TASC）。

????????本文的主要貢獻如下：

首先，我們首次設計了一種用于協作通信的真實拍賣方案，命名為TASC。TASC 隱含地使得參與代理以誠實報價或出價成為占優策略，從而消除了對市場操縱的擔憂以及針對他人進行策略博弈的開銷。其次，除了真實性之外，TASC還具備個體理性和預算平衡的特性。據我們所知，這也是經濟文獻中首個真實性的多物品雙側拍賣方案。我們希望我們的研究能夠引起更多研究人員對該類拍賣的關注。第三，TASC允許拍賣方根據性能需求選擇任意中繼分配算法。例如，可以使用最大加權匹配算法來最大化總容量；使用算法ORA [20]來最大化最小容量；或者使用最大匹配算法來最大化成功交易的數量。最后但同樣重要的是，大量的實驗驗證了TASC的真實性，并表明TASC在系統效率上僅有有限的下降，但仍能滿足所有要求的特性。

RELATED WORK

????????盡管拍賣理論在經濟學文獻中已得到廣泛研究，但現有的拍賣設計無法完全滿足第1節中所提出的各項要求。我們在表1中總結了最相關的工作。在該表中，我們列出了現有工作與本文所設計拍賣方案之間的主要差異。其中，交易物品的異質性在拍賣設計中起到了重要作用，使得設計更具挑戰性，因為每個買家對來自不同賣家的不同物品具有不同的偏好。除了表格中列出的差異之外，一些現有方案還采用了多輪拍賣機制[6, 2, 15]。然而，多輪拍賣并不適用于協作通信場景，因為在協作通信中，及時性是一個必要條件，而較大的通信開銷則不可取。

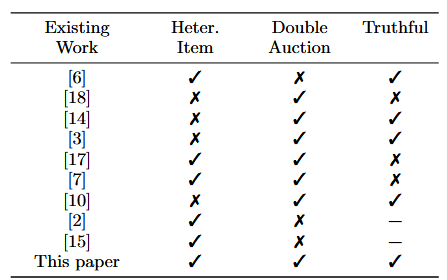
表1：現有的拍賣方案。“?”表示相應屬性未知。

3. PRELIMINARIES AND PROBLEM FORMULATION

3.1 Cooperative Communications

我們使用圖2中一個著名的三節點示例來描述協作通信（CC）的本質。在這個示例中，s是發送信息的源節點，d是接收信息的目的節點，而r是中繼節點，它既接收又轉發信息，以增強源節點和目的節點之間的通信。協作通信以幀為單位進行，每幀被劃分為兩個時隙。在第一個時隙中，源節點s向目的節點d傳輸數據。由于廣播特性，中繼節點r可以監聽到這一傳輸。在第二個時隙中，r根據不同的協作通信模式，采用不同的技術將數據轉發給d。協作通信有兩種模式：放大轉發（AF）和解碼轉發（DF）[13]。關于AF和DF的詳細內容，請感興趣的讀者參考文獻[13]。我們用cR(s,r,d)表示協作通信下的可達容量，用𝑐D(s,d)表示無協作通信下的可達容量。

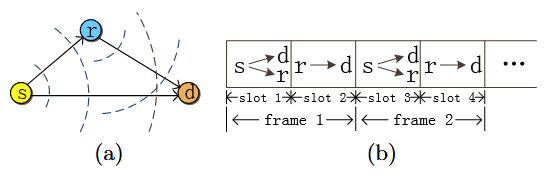
圖2：CC的三個節點示例

3.2 Problem Model

????????本文考慮一個由 $n$ 個源-目的地對 $\{s_1, d_1; s_2, d_2; \dots; s_n, d_n\}$ 和 $m$ 個中繼節點集合 $R = \{r_1, r_2, \dots, r_m\}$ 組成的靜態自組織無線網絡。我們用 $\mathcal{S} = \{s_1, s_2, \dots, s_n\}$ 表示源節點集合，用 $\mathcal{D} = \{d_1, d_2, \dots, d_n\}$ 表示目的節點集合。我們假設存在一個基站作為中央控制器，并在拍賣機制中充當拍賣人角色，例如在蜂窩網絡中，基站即為所有源節點 $s_i$ 的基站，如圖1所示。

????????我們將協作通信拍賣設計為一輪多物品雙向拍賣。在此拍賣中，源節點是買家，中繼節點是賣家，基站是拍賣人。在本文中，我們可能會交替使用“源節點”與“買家”，“中繼節點”與“賣家”，以及“基站”與“拍賣人”。為了敘述方便，我們一般將買家和賣家統稱為代理。買家為協作通信的中繼服務出價，而賣家則以消耗資源（例如能量）為代價提供協作服務，并獲得相應的貨幣支付。對于每個買家而言，由于與不同中繼節點協作可實現不同的容量，因此其對各個中繼節點的估值也有所不同。令 $\mathcal{V}_{j}^{i}$ 表示買家 $\mathcal{s}_i$ 對來自賣家 $\mathcal{r}_j$ 的中繼服務的真實估值，即 $\mathcal{s}_i$ 愿意為該中繼服務支付的真實價格。令 $\mathbf{V}_i = (\mathcal{V}_1^i, \mathcal{V}_2^i, ..., \mathcal{V}_m^i)$ 表示買家 $\mathcal{s}_i$ 的真實估值向量。顯然，當 $\mathcal{c}_{R}(\mathcal{s}_i, \mathcal{r}_j, \mathcal{d}_i) > \mathcal{c}_{D}(\mathcal{s}_i, \mathcal{d}_i)$ 時，有 $\mathcal{V}_j^i > 0$ ；否則 $\mathcal{V}_j^i = 0$ 。買家沒有動機購買無法提供比直接傳輸更高容量的中繼服務。類似地，令 $\mathcal{C}_j$ 表示賣家 $\mathcal{r}_j$ 提供中繼服務的真實成本，例如與能耗相關。賣家不會區分不同的買家，因為它使用相同的發射功率。我們假設每個買家最多只需要一個中繼節點來協助協作通信。Zhao等人[23]最近的一項研究表明，即使存在多個可用的中繼節點，源節點只需選擇最佳的中繼節點即可實現完全分集增益。我們還假設每個中繼節點最多只能被一個源節點共享，否則它所提供的容量將不同于買家所期望的值。

????????該拍賣是一個密封投標拍賣。根據拍賣理論中的術語，我們將買方提交的價格稱為出價（bid），賣方提交的價格稱為要價（ask）。每個買方（或賣方）向拍賣人提交其私有的出價（或要價），且不知道其他人的出價信息。我們假設所有要價和出價都是靜態的，在拍賣過程中不會發生變化。在拍賣開始時，每個買方 $\mathcal{S}_i$ 提交一個出價向量 $\mathbf{B}_i = (B_{1i}, B_{2i}, \dots, B_{mi})$ ，其中 $B_{ji}$ 表示買方 $\mathcal{S}_i$ 對賣方 $\mathcal{R}_j$ 的出價。 $\mathbf{B}_i$ 可能與其真實估值向量 $\mathbf{V}_i$ 相同，也可能不同。每個賣方 $\mathcal{R}_j$ 提交其要價 $A_j$ ，該要價可能與其真實成本 $C_j$ 相同，也可能不同。令 $\mathbf{B} = (B_1; B_2; \dots; B_n)$ 表示由所有買方提交的出價向量組成的出價矩陣。類似地，令 $\mathbf{A} = (A_1, A_2, \dots, A_m)$ 表示由所有賣方提交的要價組成的集合。記 $\mathbf{B}_{-j}^i = (B_{1i}, \dots, B_{j-1i}, B_{j+1i}, \dots, B_{mi})$ 為買方 $\mathcal{S}_i$ 的出價向量，其中 $B_{ji}$ 被移除。記 $\mathbf{B}_{-i} = (B_1; \dots; B_{i-1}; B_{i+1}; \dots; B_n)$ 為出價矩陣，其中 $\mathcal{S}_i$ 的出價向量 $\mathbf{B}_i$ 被移除。記 $\mathbf{B}|_{iB}$ 為出價矩陣，其中 $\mathcal{S}_i$ 的出價向量被替換為 $B$ 。類似地，定義 $\mathbf{A}_{-j}$ 和 $\mathbf{A}|_{jA}$ 。給定 $\mathcal{S}$ 、 $\mathcal{R}$ 、 $\mathcal{D}$ 、 $\mathbf{B}$ 和 $\mathbf{A}$ ，拍賣人根據設計的拍賣方案決定獲勝者（包括獲勝買方和獲勝賣方），將中繼節點分配給源節點，并確定獲勝買方和獲勝賣方的清算價格。設 $\mathcal{S}_w \subseteq \mathcal{S}$ 獲勝買方的集合， $\mathcal{R}_w \subseteq \mathcal{R}$ 為獲勝賣方的集合。令 $\sigma: \{i : \mathcal{S}_i \in \mathcal{S}_w\} \to \{j : \mathcal{R}_j \in \mathcal{R}_w\}$ 為拍賣人決定的中繼節點分配。注意， $\sigma(\cdot)$ 實際上是從獲勝買方索引到獲勝賣方索引的一一映射。因此， $\sigma^{-1}(j)$ 是中繼節點 $\mathcal{R}_j$ 所分配的源節點的索引。設 $P_b^i$ 為獲勝買方 $\mathcal{S}_i$ 需要支付的價格。設 $P_s^j$ 為拍賣人支付給獲勝賣方 $\mathcal{R}_j$ 的付款。則買方 $\mathcal{S}_i \in \mathcal{S}$ 的效用定義為：

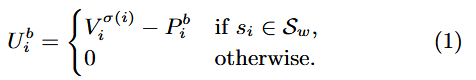
相應地，賣方 $\mathcal{R}_j \in \mathcal{R}$ 的效用定義為：

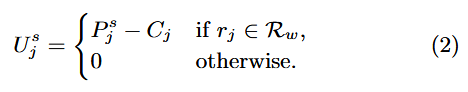
本文中的符號總結見表2。

表二符號表

3.3 Economic Properties

拍賣方案的設計在很大程度上取決于所期望的特性。在下文中，我們介紹四種最常見的經濟特性： ?

誠實性：如果對于每個買方（或賣方）而言，披露真實的私人估值（或成本）是占優策略，則該拍賣是誠實的。換句話說，無論其他參與者如何出價，任何買方（或賣方）都無法通過提交與其真實估值（或成本）不同的報價（或要價）來提高自身的效用。
個體理性（Individual Rationality）：若沒有獲勝的買方支付的價格超過其出價，且沒有獲勝的賣方獲得的支付低于其要價，則該拍賣是個體理性的。即對所有? $s_i \in S_w$ 與 $r_j \in \mathcal{R}_w$ 有 $B_i^{\phi(i)} \;\geq\; P_i^b, \qquad A_j \;\leq\; P_j^s.$ 該性質確保了源節點與中繼節點都有動力參與協作通信。
預算平衡（Budget Balance）：若所有買方的總支付金額不小于支付給所有賣方的總金額，則該拍賣是預算平衡的，即： $\sum_{s_i \in S_w} P_i^b \geq \sum_{r_j \in \mathcal{R}_w} P_j^s$
系統效率（System Efficiency）：若拍賣能優化所有參與者估值的總和，則該拍賣是系統高效的。在本文的上下文中，系統效率等價于總容量最大化。

3.4 Objective

????????設計一種同時滿足前一節所述全部四種性質的拍賣方案是可取的。然而，文獻[16]中的一個著名結果表明，即使不考慮個體理性，也不存在任何雙重拍賣機制能夠同時實現真實性、預算平衡和效率。我們的最終目標是設計一種拍賣方案，既能激勵中繼節點和源節點參與協作通信，又能防止任何代理通過操縱其出價或要價來操控市場。因此，在犧牲系統效率的情況下，優先設計具備前三種性質的拍賣方案具有最高重要性。這種方法論也被現有的多重拍賣廣泛采用[3, 7, 10, 24]。

總之，我們的目標是設計一個用于協作通信（Cooperative Communications, CC）的真誠拍賣方案（TASC），記為： $\Psi = (S, \mathcal{R}, D, \mathbb{B}, A)$

其中，給定 $S, \mathcal{R}, D, \mathbb{B}, A$ 拍賣師需要確定：

獲勝買方集合 $S_w$
獲勝賣方集合 $\mathcal{R}_w$
中繼分配映射 $\sigma$
每個買方的支付價格 $P_i^b$
以及每個賣方的支付金額 $P_j^s$

并滿足以下條件：

對于每個買方 $s_i$ ，其效用 $U_i^b$ 在出價為 $V_i$ 時達到最大；
對于每個賣方 $r_j$ ，其效用 $U_j^s$ 在要價為 $C_j$ 時達到最大。

對于每個買方 $s_i$ ，有 $B_i^{\sigma(i)} \geq P_i^b,$
對于每個賣方 $r_j$ ，有 $A_j \leq P_j^s.$

- 預算平衡條件：
$\sum_{s_i \in S_w} P_i^b \geq \sum_{r_j \in \mathcal{R}_w} P_j^s.$

4. CHALLENGES OF COOPERATIVE COMMUNICATION AUCTION DESIGN

在本節中，我們闡述了設計誠實合作通信拍賣所面臨的挑戰。為了更好地理解這些挑戰，我們展示了現有雙重拍賣機制直接應用于合作通信拍賣時的失敗情況。現有的雙重拍賣機制有兩種，即基于VCG的雙重拍賣和McAfee雙重拍賣。我們分別在第4.1節和第4.2節對這兩種機制進行了分析。

4.1 基于 VCG 的雙邊拍賣

VCG（Vickrey–Clarke–Groves）可以保證真誠性。在基于 VCG 的雙邊拍賣中，贏家與買賣匹配的確定方式是使社會福利最大化： $W = \sum_{s_i \in S_w} \big( B_i^{\phi(i)} - A_{\phi(i)} \big)$

直觀地，這可通過在二分圖 $G = (S, \mathcal{R}, \mathcal{E}, \omega)$ 上求最大權匹配實現；其中若 $B_i^{j} > 0$ 則 $(s_i, r_j) \in \mathcal{E}$ 且邊權 $\omega(s_i, r_j) = B_i^{j} - A_j.$ 記 $W^*$ 為最優值， $W^*_{-s_i}$ 為移除買方 $s_i$ 后的最優值， $W^*_{-r_j}$ 為移除賣方 $r_j$ 后的最優值。則每個贏家買方的支付為（式(3)）： $P_i^b = B_i^{\phi(i)} - ( W^* - W^*_{-s_i} ).$

每個贏家賣方獲得的支付為（式(4)）： $P_j^s = A_j + ( W^* - W^*_{-r_j} ).$ 由此可見 $W^* - W^*_{-s_i} \ge 0,\; W^* - W^*_{-r_j} \ge 0$ 成立，因而個體理性成立；VCG 亦是真誠的。
但圖 3 給出預算不平衡的反例： $W^* = 9,\; W^*_{-s_1} = 4,\; W^*_{-s_2} = 7,\; W^*_{-r_1} = 7,\; W^*_{-r_2} = 3,$

據此 $P_1^b = 10-(9-4) = 5,\quad P_2^b = 4-(9-7) = 2,$ $P_1^s = 2+(9-7) = 4,\quad P_2^s = 3+(9-3) = 9,$

拍賣師虧損 $(4+9) - (5+2) = 6.$ 這說明 VCG 雙邊拍賣不預算平衡，不適合直接用于協作通信。

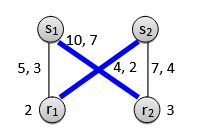
圖3：一個展示基于 VCG 的雙邊拍賣預算失衡的示例。與連邊 $(s_i, r_j)$ 相關的兩個數值分別為出價 $B_i^j$ 與權重 $\delta(s_i, r_j)$ 。加粗的藍色連線表示最大權匹配。每個賣方節點旁邊的數字是該賣方的要價

4.2 McAfee 雙邊拍賣

McAfee 拍賣假設拍賣物品同質：買方無差異偏好。因而每個買方僅報一個出價，每個賣方僅報一個要價。流程為：將買方出價按非增序、賣方要價按非減序排序：

$B_{i_1} \ge B_{i_2} \ge \dots \ge B_{i_n},\quad A_{j_1} \le A_{j_2} \le \dots \le A_{j_m}.$

找最大k使得

$B_{i_k} \ge A_{j_k}\quad \text{and}\quad B_{i_{k+1}} < A_{j_{k+1}}.$ 令 $t = \frac{B_{i_{k+1}} + A_{j_{k+1}}}{2}.$

結算價規則：

$\{\, P^b = P^s = t \text{ if } A_{j_k} \le t \le B_{i_k},\;\; P^b = B_{i_k},\; P^s = A_{j_k} \text{ otherwise} \,\}.$

該機制可同時滿足真誠性、個體理性與預算平衡；但由于協作通信中的“中繼—源”異質性強（不同中繼對不同源的容量增益不同），同質物品假設不成立，因此 McAfee 機制不能直接應用于協作通信，需要進一步的機制設計改造。

5. 我們的拍賣方案

????????在本節中，我們提出了TASC，一種針對協作通信的誠實且計算高效的拍賣方案。我們首先簡要概述其設計原理，然后詳細描述該方案的兩個主要階段。我們通過一個示例來幫助理解TASC。接下來，我們證明TASC滿足第3.4節末尾列出的三個性質。最后，我們證明TASC的時間復雜度為多項式時間 $\mathcal{O}(\mathcal{T} + l^3)$ ，其中 $\mathcal{T}$ 是中繼分配算法的時間復雜度， $l = \min\{n, m\}$ 。

5.1 概述

????????盡管基于VCG的雙重拍賣在表面上最接近我們所要設計的拍賣，但其預算失衡對拍賣人來說是不可接受的。相比之下，TASC的設計靈感來源于McAfee雙重拍賣。TASC包含兩個階段：分配階段和勝者確定與定價階段。為了克服McAfee雙重拍賣的局限性，我們在分配階段應用了一種分配算法來尋找中繼分配。在第二階段，我們為賣方和買方戰略性地確定清算價格，而不是簡單地將出價和要價對齊，以避免在最終勝者選擇中出現低效的中繼分配。與McAfee雙重拍賣類似，拍賣人向所有中標買方收取相同的價格，并向所有中標賣方支付相同的款項。

5.2 設計 ?

????????分配階段

????????我們現在詳細描述TASC的設計。在分配階段，我們需要設計一種新的中繼分配算法，或者應用現有的中繼分配算法，并要求其與買方的出價和賣方的要價無關。中繼分配算法對出價或要價的依賴可能會使拍賣容易受到市場操縱的影響。我們在算法1中展示了分配階段的流程。

初始化邊集 $\mathcal{E} \leftarrow \varnothing$

4–7. 為所有“買方—中繼”二元組檢查是否有增益，若有則連邊
判據：中繼真的有用（協作容量大于直傳容量）： $c_R(s_i, r_j, d_i) > c_D(s_i, d_i)$ 若成立，加入邊： $\mathcal{E} \leftarrow \mathcal{E} \cup \{(s_i, r_j)\}$

8–9. 在得到的二分圖上，調用與報價無關的分配算法

$S_c$ 、 $\mathcal{R}_c$ ：候選贏家買方/賣方集合（滿足一對一匹配的子集）
：分配映射（把每個買方指派給一個中繼）
可選擇不同目標：
- 最大權匹配（MWM）：最大化總容量
- 最大匹配（MM）：最大化成交對數
- ORA：最大化最小容量（公平性)

$\sigma \equiv \phi$ ?中繼分配映射

返回結果

????????根據具體場景，拍賣師可針對不同目的選擇不同的分配算法（Φ(?)）。例如，為最大化總容量，可采用最大加權匹配算法；為最大化所有源節點中的最小容量，可采用文獻[20]中的算法ORA；為最大化交易數量，則可使用最大匹配算法來實現。返回值包括候選中標買方 $S_c$ 、候選中標賣方 $R_c$ 以及分配 $\sigma$ 。

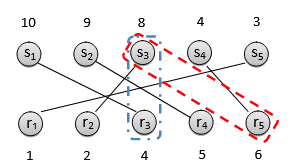
圖4：更好的勝者確定與定價。選擇藍色虛點線中的邊界對不會產生任何勝者對。選擇紅色虛線方框中的邊界對會產生兩個勝者對。

勝者確定與定價階段????????

????????在勝者確定與定價階段，我們將勝者確定與定價操作緊密集成。利用上一階段得到的分配結果，一個直觀的想法是應用McAfee雙重拍賣來確定勝者和清算價格。然而，在尋找合適的賣方-買方對時進行簡單匹配，并未考慮賣方與買方之間的映射關系。圖 4 的例子表明，存在一種更好的方法來確定贏家與清算價格。我們不是只考慮買賣對 $s_{i_k}-r_{j_k}$ ，而是再執行兩個步驟：首先，固定 $s_{i_k}$ ，尋找最大的 y 使得 $B_{i_k}^{\phi(i_k)} \ge A_{j_y}$ ；接著，固定 $r_{j_k}$ ，尋找最大的 x 使得 $B_{i_x}^{\phi(i_x)} \ge A_{j_k}$ 。我們比較兩種結果并返回更優者。其詳細算法見算法 2。

為便于說明，我們引入更多記號與概念：

記 S 為按買方在其被指派中繼上的出價非增序排列得到的有序買方列表。
記 $\mathbb{R}$ 為按賣方要價非減序排列得到的有序賣方列表。
$S_k$ 表示 S 的前 k個買方所構成的子列表。
$\mathbb{R}_k$ 表示 \ $\mathbb{R}$ 的前 k?個賣方所構成的子列表。
$\Sigma(S,\mathbb{R})$ 表示由 S 與 $\mathbb{R}$ 誘導的匹配集合，即
$\Sigma(S,\mathbb{R})=\{(s_i,r_j):\, s_i\in S,\; r_j\in \mathbb{R},\; j=\sigma(i)\}.$
我們稱拍賣師據以確定贏家與清算價格的買賣對為邊界對（boundary pair）。在第 4 節的 McAfee 雙邊拍賣中， $s_{i_k}-r_{j_k}$ ?即為一例。
由于贏家買方與贏家賣方是成對確定的，我們稱 $(s_i, r_{\sigma(i)})$ 或 $(s_{\sigma^{-1}(j)}, r_j)$ 為贏家對（winning pair）。

$S_k=\{s_{i_1},\ldots,s_{i_k}\},\qquad \mathbb{R}_k=\{r_{j_1},\ldots,r_{j_k}\}$ $\Sigma(S,\mathbb{R})=\{(s_i,r_{\sigma(i)}):\ s_i\in S,\ r_{\sigma(i)}\in\mathbb{R}\}$

Step 4 找“最大可成交前綴”索引k

$k=\max\{t:\ B_{i_t}^{\sigma(i_t)}\ge A_{j_t}\}$

Step 5 薄市場直接返回

$\text{if } k<2 \text{ then return }(S_w,\ \mathcal{R}_w,\ 0,\ 0)$

Step 6 邊界兩側擴展（ $\alpha$ , $\beta$ ）

$\alpha=\max\{t:\ B_{i_t}^{\sigma(i_t)}\ge A_{j_k}\},\qquad \beta =\max\{t:\ B_{i_k}^{\sigma(i_k)}\ge A_{j_t}\}$

Step 7 選擇“邊界對” (x,y)（二選一使后續可配數最多）

$(x,y)=\arg\max_{(i,j)\in\{(\alpha,j_k),(i_k,\beta)\}} \ \big|\Sigma(S_{i-1},\mathbb{R}_{j-1})\big|$

Step 9 統一定價

$P^b \leftarrow B_x^{\sigma(x)},\qquad P^s \leftarrow A_y$

Step 10–11 犧牲邊界買／賣各一名（去邊界對）

$S_w \leftarrow S_x \setminus \{s_x\},\qquad \mathcal{R}_w \leftarrow \mathbb{R}_y \setminus \{r_y\}$

Step 12–18 只保留“仍能配成對”的贏家（集合推導，避免量詞）

$S_w \leftarrow \{\, s_i \in S_x \setminus \{s_x\} \;:\; r_{\sigma(i)} \in \mathbb{R}_y \setminus \{r_y\} \,\}$

$\mathcal{R}_w \leftarrow \{\, r_j \in \mathbb{R}_y \setminus \{r_y\} \;:\; \sigma^{-1}(j) \in S_w \,\}$

（可選）把贏家配對集合寫清楚

$\text{Pairs}_w = \{\, (s_i, r_{\sigma(i)}) : s_i \in S_w \,\}$

Step 19 返回

$\text{return }(S_w,\ \mathcal{R}_w,\ P^b,\ P^s)$

一句總結

先排序找邊界?k，再雙向擴展得 (α,β)，二選一取最優邊界對 (x,y)；
用邊界對確定統一價 $P^b, P^s$ ，去掉邊界后，以 $\sigma$ 為準保留仍能成對者；
輸出 $(S_w,\mathcal{R}_w,P^b,P^s)$ ，兼顧真誠、個體理性與預算不虧，在給定分配候選下盡量多成對。

一句話先懂它在干嘛

上一階段（Algorithm 1）已經告訴我們：誰可以跟誰配（由 σ 記錄），并給出一批候選買家/賣家。
這一階段的目標是：
1. 挑贏家（哪些對真的成交）；
2. 定統一價（所有贏家買家同一個價 $P^b$ ，所有贏家賣家同一個價 $P^s$ ）。
為了“真誠 + 不虧”，要做三件關鍵事：
A. 把買家按“自己那條配對線上的出價”從高到低排，把賣家按要價從低到高排——兩排面對面對齊；
B. 找到邊界位置?k：前 k 對還能成交，再往后就不行；
C. 在邊界處做一個小小的取舍：只保留能讓“剩下可成對的數量最多”的那一側邊界（并犧牲掉邊界那一買一賣），這樣既能定出統一價，又避免被人“卡邊界”操縱價格。

通俗理解：

兩隊排好：
左邊是買家，從“出價高”到“出價低”；右邊是賣家，從“要價低”到“要價高”。但注意：買家的出價只看他被 σ 指定的那個賣家上的那一項（別的都忽略）。

找邊界 k：
從第一對開始一一對齊看：左邊這位的出價是不是 ≥ 右邊那位的要價？如果是，就繼續往下，比到第 k?位還成立；到第 k+1位第一次不成立。這個 k 就是“還能成交到哪兒”。
左右各試一次“向外擴”：
邊界在第 k 對。現在做兩次“假如”：
- 固定買家 $s_{i_k}$ ?? 不動，試著把右邊賣家再往后納（多看幾個便宜/不太貴的賣家），看他還能“罩住”到第幾個；這得到一個索引 β。
- 固定賣家 $r_{j_k}$ 不動，試著把左邊買家再往下納（多看幾個出價還夠高的買家），看能“撐住”到第幾個；這得到一個索引 α。
二選一：
我們現在有兩種“邊界候選”： $(i_k,\beta)$ （固定買家，擴賣家）和 $(\alpha,j_k)$ （固定賣家，擴買家）。
規則是：選那一個能讓“去掉邊界那一買一賣之后，前綴里還能配成最多對”的方案。這一步只是為了讓成交對數盡可能多。
統一價：
選定的“邊界對”是 (x,y)。
- 所有贏家買家都按邊界買家的那條出價付錢： $P^b = B_x^{\sigma(x)}$ ?；
- 所有贏家賣家都按邊界賣家的要價收錢： $P^s = A_y$ 。
  直覺：這樣基本能保證 $P^b \ge P^s$ ，平臺就不虧。
犧牲邊界對（關鍵！）：
把邊界買家 $s_x$ 和邊界賣家 $r_y$ 都刪除。這一步的意義是：
- 讓任何單個買家/賣家改報價也不會把自己變成“決定價格的人”，從而把“卡邊界操縱價格”的動機掐掉；
- 這正是“真誠”能成立的關鍵。
只留下還能按 σ 配成對的贏家：
刪了邊界那一買一賣后，可能有些人沒對象了；把沒對象的都丟掉，剩下的就是贏家對（一一對應）。

舉例

TASC 的主算法見 Algorithm 3。

5.3 一個說明性示例

????????我們使用一個簡單的示例來說明TASC的思想。可實現容量矩陣，同時也是出價矩陣，如表3(a)所示，而要價向量如表3(b)所示。

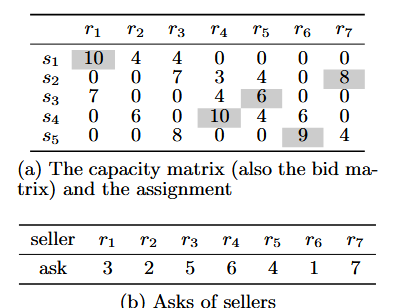
表3：一個包含5個源-目的地對和7個中繼節點的例子。

????????在指派階段，我們假設拍賣師采用最大權匹配算法。得到的指派在表 3(a) 中以高亮標注，例如，賣方 r1 被指派給買方 s1。我們把該指派畫成二分圖，如圖 5，其中各節點按其出價或要價排序。對應序列為S = ? s1, s4, s5, s2, s3 ?，? = ? r6, r1, r5, r4, r7 ?。

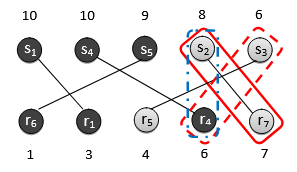
圖5：展示TASC中勝者確定與定價階段的二分圖。

????????在“贏家確定與定價”階段，拍賣師首先得到 k = 4。隨后考察配對 s2–r7 與 s3–r4，并選擇 s2–r7 作為邊界對。因此，贏家對包括 (s1, r1)、(s4, r4) 與 (s5, r6)。每個贏家買方需支付的價格為 $P^b = 8$ ，每個贏家賣方獲得的支付為 $P^s = 7$ 拍賣師的利潤為 $3 \times (8 - 7) = 3$ 。

5.4 經濟性質的證明

在給出 TASC 的詳細設計之后，我們現在證明第 3.4 節所述的目標經濟性質。

定理 1（個體理性）。 TASC 是個體理性的。□

證明:對任一贏家買方 $s_i \in S_w \in S_x$ ，滿足 $B_i^{\phi(i)}\geqslant B_x^{\phi(x)} = P^b$ 。對賣方同理。證畢。

定理 2（預算平衡）。 TASC 是預算平衡的。□

證明。 由指派可知 $|S_w| = |\mathcal{R}w|$ 。對任一贏家買方 $s_i$ ∈ $S_w$ 及其對應贏家賣方 $r{\phi(i)}$ ∈ $\mathcal{R}w$ ，均有 $P_i^b = P^b = B_x^{\phi(x)} \geqslant A_y = P^s = P_j^s$ 。于是
$\sum_{s_i \in S_w} P_i^b - \sum_{r_j \in \mathcal{R}_w} P_j^s = |S_w|(P^b - P^s) \ge 0$ 。證畢。

定理 3（真誠性）。 TASC 是真誠的。□

在證明該定理之前，我們先給出一系列引理：

我們在引理 1 中表明每個買方的拍賣結果部分獨立于其自身投標；

在引理 2（對應買方）與引理 3（對應賣方）中表明贏家確定過程分別具有投標單調性與要價單調性；

在引理 4（買方）與引理 5（賣方）中表明定價分別獨立于其自身投標/要價；

最后在引理 6（買方）與引理 7（賣方）中證明 TASC 的真誠性。

這里以后，我們用“波浪號”來區分含義相同但取值不同的記號；例如，

例如：和 $B_i$ 表示買方 $s_i$ 的兩個不同的投標向量。
另外，我們定義三個比較算子：、、。約定如下：

當時，記為 $\tilde{B}_i >_j B_i$ ；
當 $\tilde{B}_i^j = B_i^j$ 時，記為 $\tilde{B}_i =_j B_i$ ；
當 $\tilde{B}_i^j < B_i^j$ 時，記為。
引理 1。 若買方 $s_i$ 在指派階段被指派到中繼 $r_{\phi(i)}$ ，則 $s_i$ 的拍賣結果與其投標向量 $B_i^{-\phi(i)}$ 無關。等價地，若 $B_i^{\phi(i)} = \tilde{B}_i^{\phi(i)}$ ，則 $\Psi = (S, \mathcal{R}, D, \mathbb{B}\,|_i\, B_i, A)$ 與 $\tilde{\Psi} = (S, \mathcal{R}, D, \mathbb{B}\,|_i\, \tilde{B}_i, A).$ 的結果相同。□

證明（要點）。分配階段與出價和要價無關。在中標判定與定價階段（算法2）中，顯然中標判定以及向買方收取的價格僅取決于買方對 $r{\phi(i)}$ 的出價以及賣方的要價 A。因此，我們的引理成立。由于篇幅限制，我們將在以下引理中證明關于買方的性質，并僅對賣方證明一個性質。其他關于賣方的性質可采用與我們證明買方性質類似的方式進行證明。?

引理 2。 如果買方 $s_i$ 在 $\Psi = (S, \mathcal{R}, D, B|_i B_i, A)$ 中以出價 $B_i$ 獲勝，那么當其出價滿足 $\tilde{B}_i >_{\phi(i)} B_i$ 時，它在 $\tilde{\Psi} = (S, \mathcal{R}, D, B|_i \tilde{B}_i, A)$ 中也能獲勝。

證明。 在指派階段，由于中繼指派算法與出價和要價無關，如果 $s_i$ 在 $\Psi$ 中被指派到某個中繼節點，那么它在 $\tilde{\Psi}$ 中也會被指派到相同的中繼節點。令 $p_i$ 與 $\tilde{p}_i$ 分別表示 $s_i$ 在 S 和 $\tilde{S}$ 中的位置（示意見圖 6）。由于 $\tilde{B}_i^{\phi(i)} > B_i^{\phi(i)}$ ，因此在位置 $p_i$ 之后，S 與 $\tilde{S}$ 的順序完全相同。此外，我們知道兩者中第 4 行得到的 k 的取值也相同。因此，在贏家確定階段，中依然會選取 $s_x$ 與 $r_y$ 作為邊界對，這意味著買方 $s_i$ 在 $\tilde{\Psi}$ 中同樣是贏家。

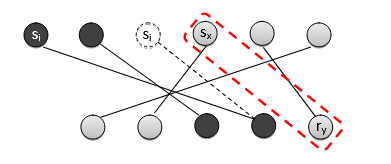
圖6：引理2的說明

引理 3。 如果賣方 $r_j$ 在 $\Psi = (S, \mathcal{R}, D, B, A|_j A_j)$ 中以要價 $A_j$ 獲勝，那么當其要價滿足 $\tilde{A}_j < A_j$ 時，它在 $\tilde{\Psi} = (S, \mathcal{R}, D, B, A|_j \tilde{A}_j)$ 中也能獲勝。□

證明。 由于中繼指派算法與出價和要價無關，在 $\Psi$ 與 $\tilde{\Psi}$ 中都被指派給同一個買方 $s_{\phi^{-1}(j)}$ 。令 $q_i$ 與 $\tilde{q}_i$ 分別為 $r_j$ 在 $\mathbb{R}$ 與 $\tilde{\mathbb{R}}$ 中的位置（示意見圖 7）。由于，因此在位置 $q_i$ 之后，與 $\tilde{\mathbb{R}}$ 的順序完全相同。此外，我們知道兩者中第 4 行得到的 k 的取值也相同。因此，在贏家確定階段， $\tilde{\Psi}$ 中依然會選取 $s_x$ 與 $r_y$ 作為邊界對，這意味著賣方 $r_j$ 在 $\tilde{\Psi}$ 中同樣是贏家。

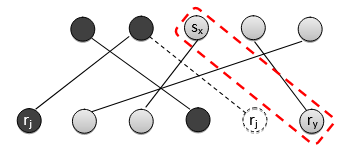
圖7：引理3的說明

引理 4。 如果在 $\Psi = (S, \mathcal{R}, D, B|_i B_i, A) and \tilde{\Psi} = (S, \mathcal{R}, D, B|_i \tilde{B}_i, A)$ 中分別以 $B_i$ 與獲勝，則其被收取的價格相同，即 $P^b = \tilde{P}^b .$

證明。 由引理 1，若買方 $s_i$ 獲勝，則其投標向量的其他分量 $B_i^{-\phi(i)}$ 不會改變拍賣結果或被收取的價格。因此，不失一般性，假設 $\tilde{B}_i >_{\phi(i)} B_i$ 。如引理 2 的證明所述， $s_x$ 與 $r_y$ 在 $\Psi$ 與中都會被選作邊界對。按定價策略可知，買方 $s_i$ 在兩種情況下被收取相同價格: $P^b = \tilde{P}^b = B_x^{\phi(x)} .$

引理 5。 如果 $r_j$ 在 $\Psi = (S, \mathcal{R}, D, B, A|_j A_j)$ 與 $\tilde{\Psi} = (S, \mathcal{R}, D, B, A|_j \tilde{A}_j)$ 中分別以 $A_j$ 與 $\tilde{A}_j$ 獲勝，則其獲得的支付相同，即 $P^s = \tilde{P}^s .$

表4：引理6的證明邏輯。w表示它獲勝，l表示它失敗。

引理 6。 TASC 對買方是真誠的。

證明。 我們通過證明：不存在任何買方能夠通過提交與其真實估值不同的投標向量來提升效用，即對任意 $B_i \ne V_i$ 均有 $\tilde{U}_i^b \le U_i^b ,$

其中 $\tilde{U}_i^b$ 與分別是 $s_i$ 在出價 $B_i$ 與 $V_i$ 時的效用。我們逐一考察表 4 所示的所有可能情況。

情況 1：。

由引理 1 可知，當 $B_i =_{\phi(i)} V_i$ 時， $s_i$ 在兩次拍賣中被收取的價格 $P^b$ 相同。因此 $\tilde{U}_i^b = V_i^{\phi(i)} - P^b = U_i^b .$

情況 2：。

由引理 2 可知，不可能出現“ 用出價獲勝、改為反而失敗”的情形。因此存在三種子情形：

$s_i$ 用 $V_i$ 與 $B_i$ 都獲勝；
用 $B_i$ 獲勝而用 $V_i$ 失敗；
$s_i$ 兩者都失敗。

對于 1)，由引理 4， $s_i$ 被收取相同價格，因此 $\tilde{U}_i^b = U_i^b = V_i^{\phi(i)} - P^b .$

對于 3)，由于兩次都失敗， $\tilde{U}_i^b = U_i^b = 0 .$

現關注 2)。既然 $s_i$ 用 $B_i$ 獲勝而用 $V_i$ 失敗，則有 $\tilde{P}^b = B_{\tilde{x}}^{\phi(\tilde{x})} \ge V_i^{\phi(i)} ,$

其中 $\tilde{x}$ 是中第 7 行所選買方的索引。于是 $\tilde{U}_i^b = V_i^{\phi(i)} - \tilde{P}^b \le 0 = U_i^b .$

情況 3：。

由引理 2 可知，不可能出現“ $s_i$ 用 $B_i$ 獲勝、改為 $V_i$ 失敗”的情形。因此亦有三種子情形：

$s_i$ 用 $V_i$ 與 $B_i$ 都獲勝；
用 $B_i$ 失敗而用 $V_i$ 獲勝；
$s_i$ 兩者都失敗。

對于 1) 與 3)，與情況 2 的分析相同，可得 $\tilde{U}_i^b = U_i^b .$

對于 2)，顯然 $\tilde{U}_i^b = 0 \quad \text{and } \quad U_i^b \ge 0 .$

我們已證明：買方無法通過提交與真實估值不同的投標向量來提升其效用。證畢。

引理 7。 TASC 對賣方是真誠的。

定理 3 的證明。 由引理 6 與引理 7 可知，TASC 對買方與賣方均真誠，從而 TASC 真誠。

5.5 時間復雜度

定理 4。 TASC 的時間復雜度為 $O(T + l^3) ,$ 其中 T 是中繼指派算法的時間復雜度，。

證明。 對于指派階段，時間復雜度取決于所使用的中繼指派算法。例如，最大權匹配算法的復雜度為 $O\big((n+m)^2 \log(n+m) + (n+m)\,n\,m\big) ,$

算法 ORA 的復雜度為 $O(n\,m^2) ,$ 而最大匹配算法的復雜度為 $O\big(\sqrt{n+m}\cdot n\,m\big) .$

????????一般地，我們用 T 表示中繼指派算法的時間復雜度。在贏家確定與定價階段，由于輸入是指派結果，買方數量與賣方數量相等。顯然，該數量小于。由于最多檢查 $O(l)$ 個買賣對，且計算贏家對需要，因此該階段的復雜度為 $O(l^3)$ 。于是，TASC 的總體時間復雜度為。

6. 數值結果 ?

????????在本節中，我們通過大量實驗來評估TASC的性能，并研究其對系統效率的經濟影響。

6.1 實驗設置（Experiment Setup）
我們考慮一個無線網絡，節點在一個 $1000 \times 1000$ 的正方形區域內隨機分布。我們沿用文獻 [20] 中相同的參數設置。令所有信道的帶寬為 $22\,\text{MHz}$ 。所有無線節點的發射功率為。在傳輸模型中，我們假設路徑損耗指數為 4，噪聲為。在協作通信中，使用 DF 模式。我們將買方數量 n 固定為 100，并將賣方數量 m 從 50 到 150 以步長 10 變化。對于每一種設置，我們隨機生成 1000 個實例并對結果取平均。所有測試在一臺 Linux 個人電腦上運行，處理器為 $2.00\,\text{GHz}$ 的 Intel Pentium，內存為 $1.5\,\text{GB}$ 。

????????在拍賣方面，我們假設買方的出價在區間 $(0, V_{\max}]$ 上均勻隨機分布，其中 $V_{\max}$ 在大多數實驗中設為 4，并在考察“出價分布對系統效率影響”的實驗中取不同的值。同樣地，我們假設賣方的要價在區間 (0, 1] 上均勻隨機分布。

????????實驗中的性能度量包括：參與者效用、拍賣師利潤、總容量、成功交易數以及所有買方中的最小容量。在所有實驗中，我們用 MWM 表示最大權匹配算法，用 MM 表示最大匹配算法。

6.2 TASC 的真誠性（Truthfulness of TASC）
為驗證 TASC 的真誠性，我們隨機選取一個買方和一個賣方，考察當他們采用不同的出價或要價時，其效用如何變化。對于買方的結果見圖 8(a)–(c)，對于賣方的結果見圖 8(d)–(f)。我們注意到：在每一種“真實估值與指派算法”的組合下，沒有任何買方（對應地，賣方）能夠通過不如實出價（對應地，要價）來提升其效用。

6.3 對利潤的影響（Impact on Profit）
盡管盈利并不是設計 TASC 的目標，但仍有必要研究不同指派算法對利潤的影響。圖 9 繪出了在采用不同中繼指派算法時拍賣師的利潤。第一個觀察是：對于三種不同的中繼指派算法，利潤都比較低，最大利潤小于 1。由于我們確定價格與支付的方式，在大多數情況下有

因此，在大多數實例中利潤為 0。另一個觀察是：隨著賣方數量的增加，利潤下降。這是因為有越來越多的賣方參與拍賣時，出現的概率更高。

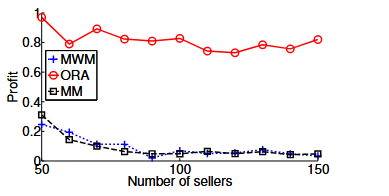
圖9：拍賣人的利潤

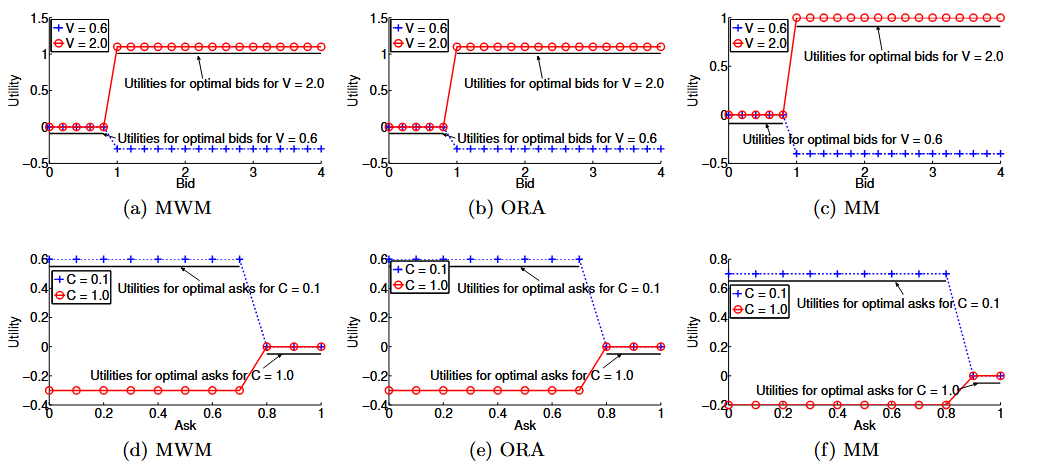
圖8：在具有不同分配算法的拍賣中，買方（(a)-(c)）和賣方（(d)-(f)）的效用，其中 $n = m = 100$ 。在每一場拍賣中， $V$ 是買方的真實估值， $C$ 是賣方的真實成本。對于買方的真實估值 $V$ 和賣方的真實成本 $C$ ，分別測試了兩個不同的值。對于每一個不同的真實估值（或成本），買方（或賣方）無法通過提交與其真實估值（或成本）不同的出價（或要約）來提高其效用。

6.4 對系統效率的影響 ?

????????根據系統性能要求的不同，系統效率可以是總容量、成功交易的數量，以及所有參與買方中的最小容量。顯然，由于拍賣師無法讓所有參與代理都成為贏家，因此與純粹的中繼分配相比，性能不可避免地會有所下降，除非采用帶有ORA的拍賣機制。當以最小容量作為系統效率時，TASC不會降低性能，因為勝者決策是基于最優結果做出的。為了捕捉經濟因素對系統效率的影響，我們在圖10(a)中繪制了TASC相對于純粹中繼分配算法的性能下降情況。令人驚訝的是，無論對于MWM還是MM，這種性能下降均與賣家數量無關。接下來，我們研究了出價分布對系統效率的影響。圖10(b)展示了在不同 $V_{\text{max}}$ 值下，TASC分別采用MWM和MM時的性能下降情況。我們觀察到，當最大出價值 $V_{\text{max}}$ 增加時，TASC相對于純粹中繼分配算法的性能下降幅度減小。換句話說，當買方對中繼節點服務的真實估值較高時，TASC能夠在顯著不降低系統效率的情況下實現所有所需的經濟特性。

6.5 運行時間

????????為了驗證我們在第5.5節中對時間復雜度的分析，我們在圖11中展示了TASC在不同分配算法下的運行時間。我們注意到，對于MWM和ORA，隨著賣家數量的增加，運行時間也隨之增加。然而，對于MM，運行時間先增加，然后在 $m = n$ 之后趨于穩定。這是因為即使 $m$ 持續增加，匹配的最大數量也受到 $n$ 的限制。

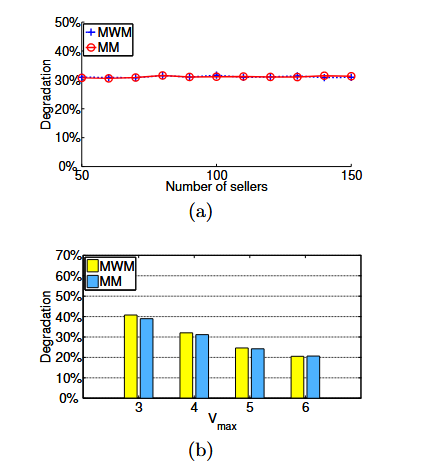
圖10：TASC相對于純中繼分配算法的系統性能下降

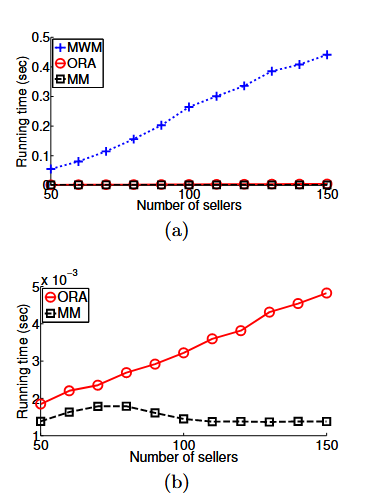
圖11：TASC的運行時間，其中n = 100，m從50到150變化。（a）和（b）使用同一組結果，而（b）為了清晰起見，展示了未使用MWM的結果。

7. 結論

????????本文設計了TASC，一種用于協作通信的誠實拍賣方案。為了激勵無線設備參與為其他設備中繼流量，TASC允許潛在的中繼節點對其中繼服務進行報價，并要求感興趣的源節點對這些報價進行出價。通過精心的設計，TASC明確地促使賣方和買方提交其真實估值，從而消除了市場操縱的擔憂以及為他人制定策略所帶來的開銷。同時，TASC還滿足個體理性與預算平衡特性。此外，TASC可以使用任意中繼分配算法以滿足不同的系統性能需求。廣泛的實驗結果證實了我們對TASC的理論分析，并表明TASC能夠在系統效率有限下降的情況下實現所有所需的經濟特性。