01 概念

?定義：二叉樹既然叫二叉樹，顧名思義即度最大為2的樹稱為二叉樹。?它的度可以為 1 也可以為 0，但是度最大為 2 。?

一顆二叉樹是節點的一個有限集合，該集合：

? ? ?① 由一個根節點加上兩棵被稱為左子樹和右子樹的二叉樹組成? ? ?

? ? ?② 或者為空

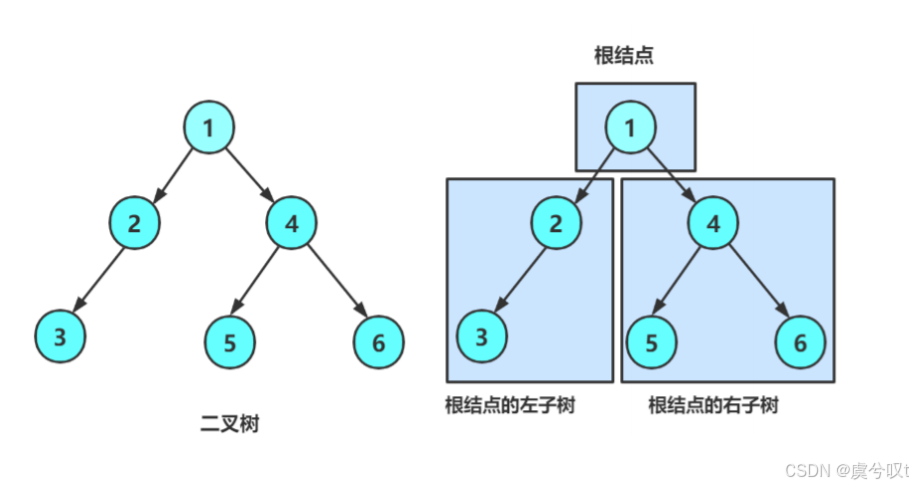
觀察上圖我們可以得出如下結論：

? ? ?① 二叉樹不存在度大于 2 的節點，換言之二叉樹最多也只能有兩個孩子。

? ? ?② 二叉樹的子樹有左右之分，分別為左孩子和右孩子。次序不可顛倒，因此二叉樹是有序樹。

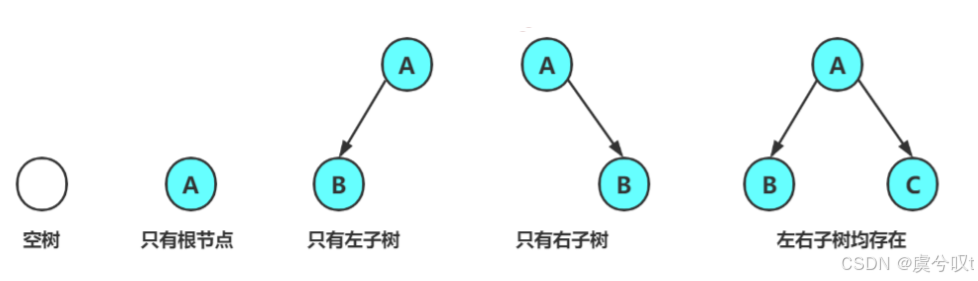
注意：對于任意的二叉樹都是由以下幾種情況復合而成的：

02 滿二叉樹

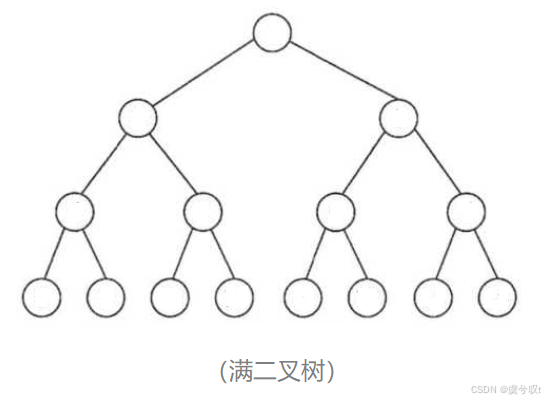
定義：一個二叉樹，如果每一層的結點數都達到了最大值（均為2），則這個二叉樹就可以被稱作為 "滿二叉樹" 。

換言之，如果一個二叉樹的層數為 h，且總結點數為 2的 h 次方 - 1，那么它就是一個滿二叉樹。

計算公式：

?① 已知層數求總數：

?② 已知總數求層數：?

03 完全二叉樹

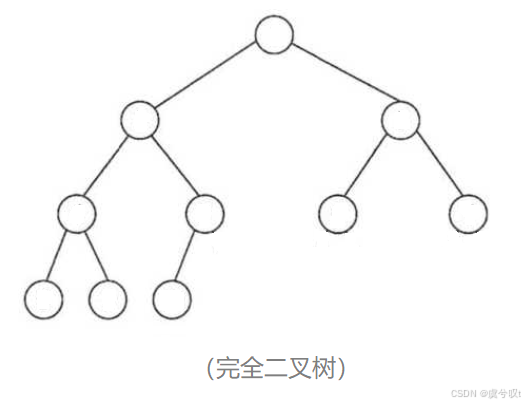
定義：對于深度為 h?的，有 n 個結點的二叉樹，當且僅當其每一個結點都與深度為 h?的滿二叉樹中編號從 1 至 n 的結點一一對應時稱之為完全二叉樹。

前 h - 1 層是滿的，最后一層不滿，但最后一層從左到右是連續的。

完全二叉樹是效率很高的數據結構，完全二叉樹是由滿二叉樹而引出來的。所以，滿二叉樹是一種特殊的完全二叉樹（每一層節點均為2）。

常識：

① 完全二叉樹中，度為 1 的最多只有 1 個。

② 高度為??的完全二叉樹節點范圍是? ???

04 二叉樹的性質

四點規則：

① 若規定根節點的層數為 1 ，則一顆非空二叉樹的第 i 層上最多有 2?的 i - 1 次方個節點。

② 若規定根節點的層數為 1 ，則深度為 h 的二叉樹最大節點數是 2 的 h 次方 - 1。

③ 對任何一棵二叉樹，如果度為 0 其葉子結點個數為 n0，度為 2 的分支節點個數為 n2，則有n0 = n2 + 1。換言之，度為 0 的永遠比度為 2 的多一個葉子結點。

假設二叉樹有 n 個結點，從總結點數角度考慮：n?= n0 + n1 + n2，從邊的角度考慮，n 個結點的任意二叉樹，總共有 n - 1 條邊。因為度為 0 的結點沒有孩子，故度為 0?的結點不產生邊; 度為 1 的結點只有一個孩子，故每個度為 1 的結點產生一條邊; 度為 2 的結點有 2 個孩子，故每個度為 2 的結點產生兩條邊，所以總邊數為： n1+2*n2，故從邊的角度考慮：n - 1 = n1 + 2*n2，?n0 + n1 + n2 = n1 + 2*n2 - 1，即：n0 = n2 + 1

④ 若規定根節點的層數為 1 ， 具有 n 個節點的滿二叉樹的深度 h = log（n + 1）。

對于具有n個結點的完全二叉樹，如果按照從上至下從左至右的數組順序對所有節點從0開始編號，則對于序號為i的結點有：

? 1. 若 i > 0，i 位置節點的雙親序號：(i - 1) / 2；i = 0，i 為根節點編號，無雙親節點。

? 2. 若2i + 1 < n，左孩子序號：2i + 1，2i + 1 >= n否則無左孩子。

? 3. 若2i + 2 < n，右孩子序號：2i + 2，2i + 2 >= n否則無右孩子。

05 二叉樹的存儲

1 數組存儲

一般情況下使用數組來存儲，只適合完全二叉樹。

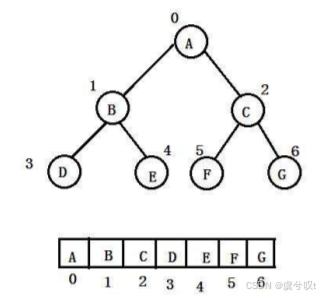
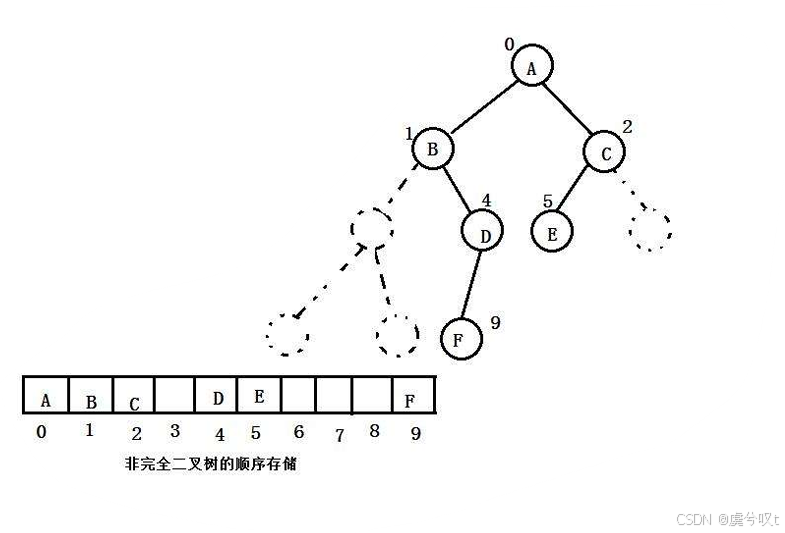
如果是非完全二叉樹，會造成空間上的浪費。

2 鏈式存儲

typedef struct BinaryTreeNode
{struct BinTreeNode* left; // 左孩子struct BinTreeNode* right; // 右孩子DataType data; // 當前節點值域
}BTree;

06 二叉樹的遍歷

二叉樹的遍歷一般有四種方法：前序遍歷，中序遍歷，后序遍歷，層序遍歷。

1 前序遍歷

先遍歷根節點，再依次遍歷左子樹，右子樹。而遍歷左子樹，又要先遍歷根節點，再依次遍歷左子樹，右子樹…直至遍歷到空樹。

// 遞歸實現
void PreOrder(BTree*root)
{if (root == NULL)return;printf("%d ", root->data);//根節點PreOrder(root->left);//左子樹PreOrder(root->right);//右子樹
}

2 中序遍歷

先遍歷左子樹，再依次遍歷根節點，右子樹。而遍歷左子樹，又要先遍歷左子樹，再依次遍歷根節點，右子樹…直至遍歷到空樹。

// 遞歸實現
void Inorder(BTree*root)
{if (root == NULL)return;PreOrder(root->left);//左子樹printf("%d ", root->data);//根節點PreOrder(root->right);//右子樹
}

3 后序遍歷

先遍歷左子樹，再依次遍歷右子樹，根節點。而遍歷左子樹，又要先遍歷左子樹，再依次遍歷右子樹，根節點…直至遍歷到空樹。

// 遞歸實現
void Postorder(BTree*root)
{if (root == NULL)return;PreOrder(root->left);//左子樹PreOrder(root->right);//右子樹printf("%d ", root->data);//根節點
}

4 層序遍歷

層序遍歷顧名思義就是一層一層地遍歷，這時就需要借助一個數據結構：隊列來輔助實現。

void leverOrder(BTree* root, Queue* pq)
{if (root == NULL)return;QueuePush(pq, root);//插入第一個節點while (!QueueEmpty(pq))//隊列不為空{BTree* p = QueueFront(pq);printf("%d ", p->val);QueuePop(pq);if (p->left != NULL)//帶入左孩子{QueuePush(pq, p->left);}if (p->right != NULL)//帶入右孩子{QueuePush(pq, p->right);}}
}