數據結構之樹結構（下）

各種各樣的大樹

平衡二叉樹 (AVL樹)

普通二叉樹存在的問題

左子樹全部為空，從形式上看，更像一個單鏈表
插入速度沒有影響
查詢速度明顯降低（因為需要依次比較），不能發揮BST的優勢，因為每次還需要比較左子樹，其查詢速度比單鏈表還慢
解決方案-平衡二叉樹(AVL)

基本介紹

平衡二叉樹也叫平衡二叉搜索樹(Self-balancing binary search tree)又被稱為AVL樹，可以保證查詢效率較高。
具有以下特點：它是一棵空樹或它的左右兩個子樹的高度差的絕對值不超過1，
并且左右兩個子樹都是一棵平衡二叉樹。平衡二叉樹的常用實現方法有紅黑樹、
AVL、替罪羊樹、Treap、伸展樹等，

應用案例

判斷樹的高度

// 返回左子樹的高度
public int leftHeight() {if (left == null) {return 0;}return left.height();
}// 返回右子樹的高度
public int rightHeight() {if (right == null) {return 0;}return right.height();
}// 返回當前結點的高度，以該結點為根結點的樹的高度
public int height() {return Math.max(left == null ? 0 : left.height(), right == null ? 0 : right.height()) + 1;
}

單旋轉（左旋轉）

左旋轉步驟

前提條件： $r i g h t He i g h t () ? l e f t He i g h t () > 1$

創建一個新的節點newNode(以root 這個值創建)，創建一個新的節點，值等于當前根節點的值，把新節點的左子樹設置了當前節點的左子樹
// newNode.left = left
把新節點的右子樹設置為當前節點的右子樹的左子樹
// newNode.right =right.left;
把當前節點的值換為右子節點的值
// value=right.value;
把當前節點的右子樹設置成當前結點的右子樹的右子樹
// right=right.right;
把當前節點的左子樹設置為新節點
// left=newLeft;

// 左旋轉
private void leftRotate() {// 1. 創建一個新的節點newNode(以root 這個值創建)// 創建一個新的節點，值等于當前根節點的值，把新節點的左子樹設置了當前節點的左子樹Node newNode = new Node(value);newNode.left = left;// 2.把新節點的右子樹設置為當前節點的右子樹的左子樹newNode.right = right.left;// 3.把當前節點的值換為右子節點的值value = right.value;// 4.把當前節點的右子樹設置成當前結點的右子樹的右子樹right = right.right;// 5.把當前節點的左子樹設置為新節點left = newNode;
}

單旋轉（右旋轉）

步驟

創建一個新的節點newNode(以root 這個值創建），創健一個新的節點，值等于當前根節點的值
把新節點的右子樹設置了當前節點的右子樹
// newNode.right right
把新節點的左子樹設置為當前節點的左子樹的右子樹
// newNode.left =left.right;
把當前節點的值換為左子節點的值
// value=left.value;
把當前節點的左子樹設置成左子樹的左子樹
// left=left.left;
把當前節點的右子樹設置為新節點
// right=newLeft;

// 右旋轉
public void rightRotate() {// 1.創建一個新的節點newNode(以root 這個值創建）// 創健一個新的節點，值等于當前根節點的值Node newNode = new Node(value);// 2.把新節點的右子樹設置了當前節點的右子樹newNode.right = right;// 3.把新節點的左子樹設置為當前節點的左子樹的右子樹newNode.left = left.right;// 4.把當前節點的值換為左子節點的值value = left.value;// 5.把當前節點的左子樹設置成左子樹的左子樹left = left.left;// 6.把當前節點的右子樹設置為新節點right = newNode;
}

雙旋轉

在單旋轉中 (即一次旋轉) 就可以將非平衡二叉樹轉成平衡二叉樹，但是在某些情況下，單旋轉不能完成平衡二叉樹的轉換

情況1??

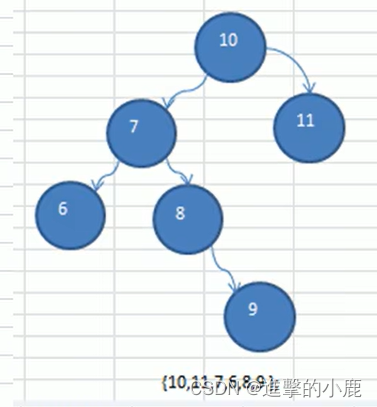
在這里插入圖片描述

實現步驟

當右旋轉的條件時
- 如果它的左子樹的右子樹高度大于它的左子樹的右子樹的高度
- 先對當前這個結點的左節點進行左旋轉
- 再對當前結點進行右旋轉
當左旋轉時
- 如果它的右子樹的左子樹高度大于它的右子樹的右子樹的高度
- 先對當前這個結點的右結點進行右旋轉
- 再對當前結點進行左旋轉

/*** 添加在Node類的添加結點的方法里邊* 每添加一個結點就判斷一次
*/
// 單旋轉
// 當添加完一個結點后，如果：(右子樹的高度-左子樹的高度) > 1，左旋轉
if (rightHeight() - leftHeight() > 1) {// 如果它的右子樹的左子樹高度大于它的右子樹的右子樹的高度if (right != null && right.rightHeight() > right.leftHeight()) {// 先對當前這個結點的右結點進行右旋轉rightRotate();}leftRotate();  // 左旋轉return; // 一定要返回，否則會出現其他問題，提高VM處理速度
}
// 當添加完一個結點后，如果：(左子樹的高度-右子樹的高度) > 1，右旋轉
if (leftHeight() - rightHeight() > 1) {// 如果它的左子樹的右子樹高度大于它的左子樹的右子樹的高度if (left != null && left.rightHeight() > left.leftHeight()) {// 先對當前這個結點的左節點進行左旋轉left.leftRotate();}rightRotate();  // 右旋轉
}

總代碼

package com.xiaolu.avl;/*** @author 林小鹿* @version 1.0*/
public class AvlTreeDemo {public static void main(String[] args) {
//        int[] arr = {4, 3, 6, 5, 7, 8};
//        int[] arr = {10, 12, 8, 9, 7, 6};int[] arr = {10, 11, 7, 6, 8, 9};AVLTree avlTree = new AVLTree();// 添加結點for (int i = 0; i < arr.length; i++) {avlTree.add(new Node(arr[i]));}// 中序遍歷avlTree.infixOrder();System.out.println("平衡處理 (左旋轉)~~~");System.out.println("樹的高度:" + avlTree.getRoot().height()); // 4System.out.println("樹的左子樹高度:" + avlTree.getRoot().leftHeight()); // 1System.out.println("樹的右子樹高度:" + avlTree.getRoot().rightHeight()); // 3System.out.println("當前根結點 = " + avlTree.getRoot());}
}// 創建AVLTree
class AVLTree {private Node root;public Node getRoot() {return root;}// 查找要刪除的結點public Node search(int value) {if (root == null) {return null;} else {return root.search(value);}}// 查找要刪除的父結點public Node searchParent(int value) {if (root == null) {return null;} else {return root.searchParent(value);}}/*** 刪除node 為根結點的二叉排序樹的最小結點的值的同時返回以node 為根結點的二叉排序樹的最小結點** @param node 傳入的結點 (當做二叉排序樹的根結點)* @return 返回以node 為根結點的二叉排序樹的最小結點的值*/public int delRightTreeMin(Node node) {Node target = node;// 循環的查找左結點，就會找到最小值while (target.left != null) {target = target.left;}// 這是target就指向了最小結點// 刪除最小結點delNode(target.value);return target.value;}// 刪除結點public void delNode(int value) {if (root == null) {return;} else {// 找到需要刪除的結點 targetNodeNode targetNode = search(value);// 如果沒有找到要刪除的結點if (targetNode == null) {return;}// 如果這顆二叉排序樹只有一個結點 (即本身就是父節點)if (root.left == null && root.right == null) {root = null;return;}// 查詢父節點Node parent = searchParent(value);// 如果待刪除的結點是葉子結點if (targetNode.left == null && targetNode.right == null) {// 刪除葉子結點// 判斷 targetNode 是父節點的左子結點還是右子節點if (parent.left != null && parent.left.value == value) {parent.left = null;} else if (parent.right != null && parent.right.value == value) {parent.right = null;}} else if (targetNode.left != null && targetNode.right != null) {// 刪除有兩顆子樹的結點int minVal = delRightTreeMin(targetNode.right);targetNode.value = minVal;} else {// 刪除只有一顆子樹的結點// 如果要刪除的結點有左子結點if (targetNode.left != null) {if (parent != null) {// 如果targetNode 是parent 的左子結點if (parent.left.value == value) {parent.left = targetNode.left;} else {// 如果targetNode 是parent 的右子結點parent.right = targetNode.left;}} else {root = targetNode.left;}} else {if (parent != null) {// 如果要刪除的結點有右子結點if (parent.left.value == value) {// 如果targetNode 是parent 的左子結點parent.left = targetNode.right;} else {// 如果targetNode 是parent 的右子結點parent.right = targetNode.right;}} else {root = targetNode.right;}}}}}// 添加結點public void add(Node node) {if (root == null) {// 如果root為空則直接讓root指向noderoot = node;} else {root.add(node);}}// 中序遍歷public void infixOrder() {if (root == null) {System.out.println("二叉樹為空，無法遍歷");} else {root.infixOrder();}}
}// 創建Node結點
class Node {int value;Node left;Node right;public Node(int value) {this.value = value;}// 返回左子樹的高度public int leftHeight() {if (left == null) {return 0;}return left.height();}// 返回右子樹的高度public int rightHeight() {if (right == null) {return 0;}return right.height();}// 返回當前結點的高度，以該結點為根結點的樹的高度public int height() {return Math.max(left == null ? 0 : left.height(), right == null ? 0 : right.height()) + 1;}// 左旋轉private void leftRotate() {// 1. 創建一個新的節點newNode(以root 這個值創建)// 創建一個新的節點，值等于當前根節點的值，把新節點的左子樹設置了當前節點的左子樹Node newNode = new Node(value);newNode.left = left;// 2.把新節點的右子樹設置為當前節點的右子樹的左子樹newNode.right = right.left;// 3.把當前節點的值換為右子節點的值value = right.value;// 4.把當前節點的右子樹設置成當前結點的右子樹的右子樹right = right.right;// 5.把當前節點的左子樹設置為新節點left = newNode;}// 右旋轉public void rightRotate() {// 1.創建一個新的節點newNode(以root 這個值創建）// 創健一個新的節點，值等于當前根節點的值Node newNode = new Node(value);// 2.把新節點的右子樹設置了當前節點的右子樹newNode.right = right;// 3.把新節點的左子樹設置為當前節點的左子樹的右子樹newNode.left = left.right;// 4.把當前節點的值換為左子節點的值value = left.value;// 5.把當前節點的左子樹設置成左子樹的左子樹left = left.left;// 6.把當前節點的右子樹設置為新節點right = newNode;}/*** 查找要刪除的結點** @param value 待刪除的結點的值* @return 如果找到則返回該結點，否則返回空*/public Node search(int value) {if (value == this.value) {return this;} else if (value < this.value) {// 如果查找的值小于當前結點，就向左子樹遞歸查找if (this.left == null) {// 如果左子樹為空return null;}return this.left.search(value);} else {// 如果查找的值不小于當前結點，向右子樹遞歸查找if (this.right == null) {// 如果右子樹為空return null;}return this.right.search(value);}}/*** 查找要刪除結點的父結點** @param value 要找到的結點的值* @return 返回的是要刪除的結點的父結點，如果沒有就返回null*/public Node searchParent(int value) {// 如果當前結點就是要刪除的結點的父節點，就返回if ((this.left != null && this.left.value == value)|| (this.right != null && this.right.value == value)) {return this;} else {// 如果查找的值小于或大于當前結點的值，并且當前結點的左子節點不為空if (value < this.value && this.left != null) {return this.left.searchParent(value); // 向左子樹遞歸查找} else if (value > this.value && this.right != null) {return this.right.searchParent(value); // 向右子樹遞歸查找} else {return null; // 沒有找到父節點}}}// 按二叉排序樹的形式遞歸添加結點public void add(Node node) {if (node == null) {return;}// 判斷傳入的結點的值與當前子樹的根結點的值關系if (node.value < this.value) {if (this.left == null) {this.left = node;} else {// 遞歸得向左子樹添加 nodethis.left.add(node);}} else { // 添加的結點的值大于當前結點的值if (this.right == null) {this.right = node;} else {// 遞歸得向右子樹添加 nodethis.right.add(node);}}// 單旋轉// 當添加完一個結點后，如果：(右子樹的高度-左子樹的高度) > 1，左旋轉if (rightHeight() - leftHeight() > 1) {// 如果它的右子樹的左子樹高度大于它的右子樹的右子樹的高度if (right != null && right.leftHeight() > right.rightHeight()) {// 先對當前這個結點的右結點進行右旋轉rightRotate();}leftRotate();  // 左旋轉return; // 一定要返回，否則會出現其他問題，提高VM處理速度}// 當添加完一個結點后，如果：(左子樹的高度-右子樹的高度) > 1，右旋轉if (leftHeight() - rightHeight() > 1) {// 如果它的左子樹的右子樹高度大于它的左子樹的右子樹的高度if (left != null && left.rightHeight() > left.leftHeight()) {// 先對當前這個結點的左節點進行左旋轉left.leftRotate();}rightRotate();  // 右旋轉}}// 中序遍歷public void infixOrder() {if (this.left != null) {this.left.infixOrder();}System.out.println(this);if (this.right != null) {this.right.infixOrder();}}@Overridepublic String toString() {return "Node[" +"value=" + value +']';}
}

多路查找樹

在這里插入圖片描述

二叉樹存在的問題

二叉樹需要加載到內存的，如果二叉樹的節點少，沒有什么問題，但是如果二叉樹的節點很多（比如1億)，就存在如下問題
問題1：在構建二叉樹時，需要多次進行 $I / O$ 操作海量數據存在數據庫或文件中)，節點海量，構建二叉樹時，速度有影響
問題2：節點海量，也會造成二叉樹的高度很大，會降低操作速度

多叉樹

在二叉樹中，每個節點有數據項，最多有兩個子節點，如果允許每個節點可以有更多的數據項和更多的子節點，就是多叉樹（multiway tree）

多叉樹通過重新組織節點，減少樹的高度，能對二叉樹進行優化

2-3樹

2-3樹是最簡單的B-樹結構，其他像2-3-4樹同理

特點

2-3樹的所有葉子節點都在同一層.（只要是B樹都滿足這個條件）
有兩個子節點的節點叫二節點，二節點要么沒有子節點，要么有兩個子節點
有三個子節點的節點叫三節點，三節點要么沒有子節點，要么有三個子節點.
2-3樹是由二節點和三節點構成的樹。

插入規則：

1）2-3樹的所有葉子節點都在同一層.（只要是B樹都滿足這個條件)
2）有兩個子節點的節點叫二節點，二節點要么沒有子節點，要么有兩個子節點

3）有三個子節點的節點叫三節點，三節點要么沒有子節點，要么有三個子節點
4)當按照規則插入一個數到某個節點時，不能滿足上面三個要求，就需要拆，先向上拆，如果上層滿，則拆本層，拆后仍然需要滿足上面3個條件。
5)對于三節點的子樹的值大小仍然遵守(BST 二叉排序樹)的規則

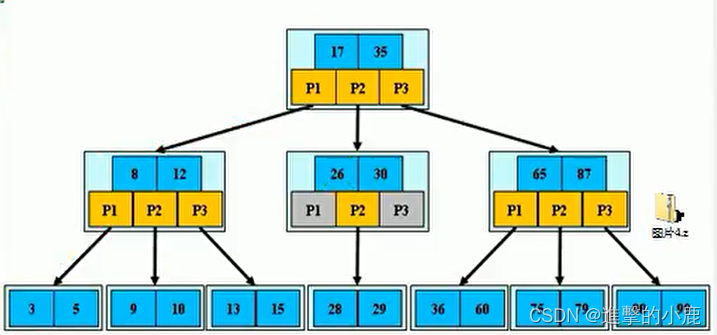
B樹

B-tree，B即Balanced

基本介紹

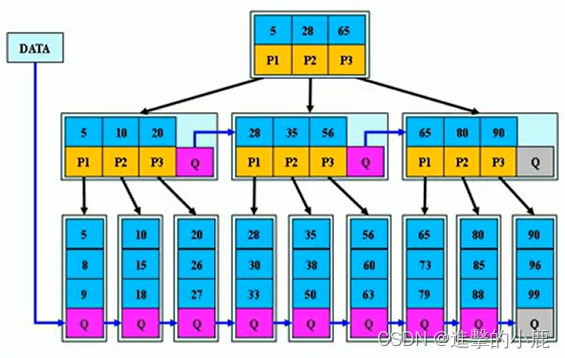
B樹的階：節點的最多子節點個數。比如2-3樹的階是3，2-3-4樹的階是4
B樹的搜索，從根結點開始，對結點內的關鍵字（有序）序列進行二分查找，如果命中側結束，否測進入查詢關鍵字所屬范圍的兒子結點；重復，直到所對應的兒子指針為空，或已經是葉子結點
關鍵字集合分布在整顆樹中，即葉子節點和非葉子節點都存放數據
搜索有可能在非葉子結點結束
其搜索性能等價于在關鍵字全集內做一次二分查找

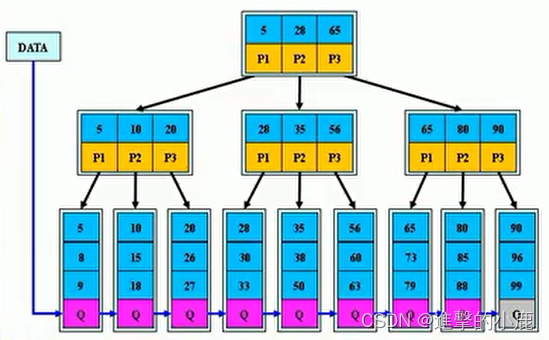
在這里插入圖片描述