
編者按
本次解讀的文章發表于 Management Science,原文信息:Hanzhang Qin, David Simchi-Levi, Li Wang (2022) Data-Driven Approximation Schemes for Joint Pricing and Inventory Control Models. https://doi.org/10.1287/mnsc.2021.4212
文章在數據驅動的前提下,研究經典的多周期聯合定價和庫存控制問題。 在此問題中,零售商定期決定其希望銷售的產品的價格和庫存水平,其目標是通過將庫存水平與隨機需求(取決于每個時期的價格)相匹配,在有限的范圍內最大化預期利潤。
鑒于需求函數或隨機噪聲分布很難準確掌握完整信息,而過去的需求數據相對容易收集,文章假設零售商對噪聲分布或真實的需求函數未知,但假設其可以訪問需求假設集,并且真實需求函數可以由需求假設集中候選函數的非負組合表示,或者真實需求函數是廣義線性的。基于此,文章提出了一種基于數據驅動的近似算法,使用預先收集的需求數據來解決聯合定價和庫存控制問題,同時證明了算法的樣本復雜度界限。在數值研究中,文章演示了如何從數據構建需求假設集,并驗證了所提出的數據驅動算法對動態問題的有效性,其結果顯著改善了與基準算法相比的最優性差距。
全信息問題以及數據驅動問題的模型和算法前文已述。本篇解讀將繼續討論原論文對算法的討論和拓展,以及數值計算實驗對算法有效性的檢驗。
1 前文回顧
1.1 模型回顧
在文章中,作者們研究了數據驅動環境下的多周期聯合定價和庫存控制問題。 根據零售商對需求和價格信息的已知程度,一般將該問題分類為全信息問題和數據驅動問題。承接前文,當零售商擁有有關隨機需求的完整信息,即 D t ( ? ) D_t(\cdot) Dt?(?)和 η t \eta_t ηt?已知時,預期利潤最大化問題就是經典的有限范圍聯合定價和庫存控制問題 P \mathcal{P} P為
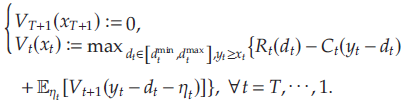
其中 V t ( x t ) V_t(x_t) Vt?(xt?)為起始庫存水平 x t x_t xt?下 t t t至 T T T期的最優期望收益。對于 t ∈ [ 1 , … , T ] t\in[1,\ldots,T] t∈[1,…,T],文章定義 U t ( y t , d t ) U_t(y_t,d_t) Ut?(yt?,dt?)為起始庫存水平 y t y_t yt?、期望需求 d t d_t dt?下 t t t至 T T T期的最優期望收益,即

令最優需求方程為

且令 W t ( y t ) W_t(y_t) Wt?(yt?)表示 t t t至 T T T期間的最優預期利潤,假設零售商將 t t t期間的庫存水平設置為 y t y_t yt?, 即
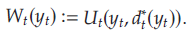
因此亦有

則最優基礎庫存清單需求策略 (base-stock list-demand policy) ( S t ? , D t ? ) (S_t^*,D_t^*) (St??,Dt??)可被定義為

依據該庫存策略,對于 t ∈ [ 1 , … , T ] t\in[1,\ldots,T] t∈[1,…,T],

對于數據驅動問題,零售商對 D t ( ? ) D_t(\cdot) Dt?(?)或 η t \eta_t ηt?未知,因此文章假設對于任意時期 t t t, 需求假設集合為 Φ t : = { D t 1 ( ? ) , … , D t K t ( ? ) } \Phi_t:=\{D_t^1(\cdot),\ldots,D_t^{K_t}(\cdot)\} Φt?:={Dt1?(?),…,DtKt??(?)}預先已知,其中未知的真實需求函數 D t ( ? ) D_t(\cdot) Dt?(?)為 Φ \Phi Φ集合內函數的線性組合。另外定義 R t k ( p t ) : = p t D t k ( p t ) R_t^k(p_t):=p_tD_t^k(p_t) Rtk?(pt?):=pt?Dtk?(pt?)及 R t k ( d t ) : = d t ( D t k ) ? 1 ( d t ) R_t^k(d_t):=d_t(D_t^{k})^{-1}(d_t) Rtk?(dt?):=dt?(Dtk?)?1(dt?)為作為所有 t t t和 k k k的 Φ t \Phi_t Φt?中的相關收益函數。原文通過假設3和4保留參數空間的線性結構以進行學習和優化,同時允許基礎需求函數具有高度非線性的形式,且確保使用價格需求樣本的回歸過程得到明確定義(最小二乘法解是唯一的)。對于任何近似算法 A \mathcal{A} A,令 D ^ t ( ? ) \hat{D}_t(\cdot) D^t?(?)和 η ^ t \hat{\eta}_t η^?t?分別為經驗預期需求函數和經驗噪聲分布,由 t ∈ [ 1 , … , T ] t\in[1,\ldots,T] t∈[1,…,T]每一個時期的歷史數據和算法 A \mathcal{A} A估計所得。令 R ^ t ( ? ) \hat{R}_t(\cdot) R^t?(?)為通過 A \mathcal{A} A所得的經驗收益函數,且定義
[ d ^ t min ? , d ^ t max ? ] : = [ D ^ t ( p t max ? ) , D ^ t ( p t min ? ) ] [\hat{d}_t^{\min},\hat{d}_t^{\max}]:=[\hat{D}_t(p_t^{\max}),\hat{D}_t(p_t^{\min})] [d^tmin?,d^tmax?]:=[D^t?(ptmax?),D^t?(ptmin?)]
為經驗期望需求的決策空間。因此有

于是定義經驗動態規劃 P ^ \hat{\mathcal{P}} P^
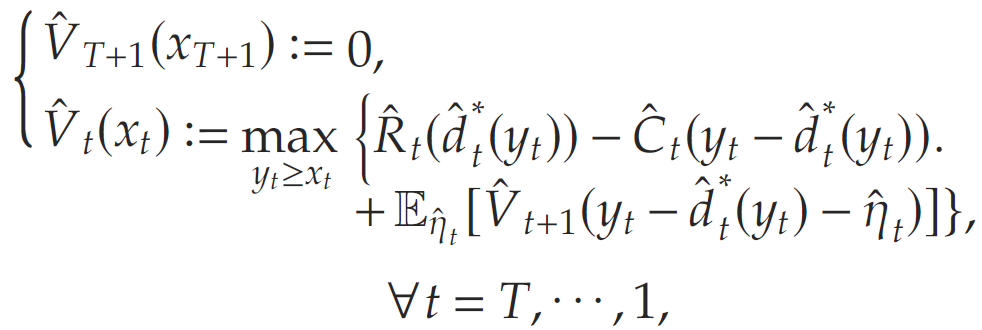
其中

同時定義經驗函數與經驗策略如下:
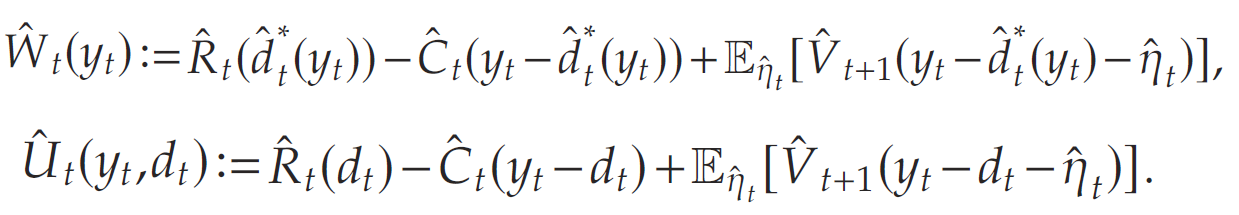
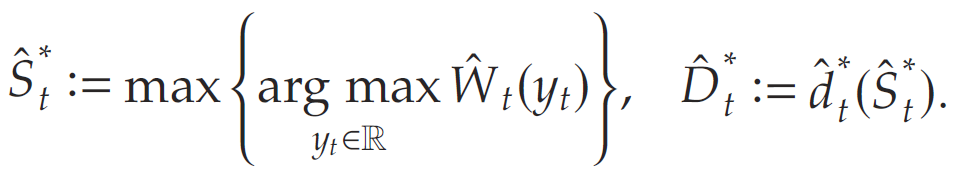
與全信息動態規劃 P \mathcal{P} P類似,經驗動態規劃 P ^ \hat{\mathcal{P}} P^可以使用后向歸納法遞歸求解。
1.2 數據驅動近似算法回顧
針對數據驅動問題,文章給出每個時期 t t t需求假設集合 Φ t : = { D t 1 ( ? ) , … , D t K t ( ? ) } \Phi_t:=\{D_t^1(\cdot),\ldots,D_t^{K_t}(\cdot)\} Φt?:={Dt1?(?),…,DtKt??(?)}以及過往價格-需求對 { ( p t 1 , d t 1 ) , … , ( p t N t , d t N t ) } \{(p_t^1,d_t^1),\ldots,(p_t^{N_t},d_t^{N_t})\} {(pt1?,dt1?),…,(ptNt??,dtNt??)},基于此二者,文章的目標是構建經驗收益函數 R ^ t ( d t ) \hat{R}_t(d_t) R^t?(dt?)與經驗分布函數 η ^ t \hat{\eta}_t η^?t?.
以下是近似算法 DDPIC 的步驟,該算法在每個時期構造經驗收入和成本函數的導數,即 R ^ t ′ ( ? ) \hat{R}'_t(\cdot) R^t′?(?)與 C ^ t r ( ? ) \hat{C}^r_t(\cdot) C^tr?(?):

關于算法的近似性能,文章根據數據驅動函數和真實函數之間導數的接近程度來討論。通過定義現定義“好”事件 E ( α ) \mathcal{E}(\alpha) E(α)和引理2-4,文章證明了模型的主要項式 R ^ t ( ? ) \hat{R}_t(\cdot) R^t?(?), C ^ t ( ? ) \hat{C}_t(\cdot) C^t?(?)和 E η ^ t [ V ^ t ( q t ? η ^ t ) ] \mathbb{E}_{\hat{\eta}_t}[\hat{V}_t(q_t-\hat{\eta}_t)] Eη^?t??[V^t?(qt??η^?t?)]在導數方面分別與 R t ( ? ) R_t(\cdot) Rt?(?), C t ( ? ) C_t(\cdot) Ct?(?)和 E η t [ V ^ t ( q t ? η t ) ] \mathbb{E}_{\eta_t}[\hat{V}_t(q_t-\eta_t)] Eηt??[V^t?(qt??ηt?)]近似,概率隨 N t N_t Nt?增長,其中 N t N_t Nt?為過往 t t t時期價格-需求對的數量,進而得到原文定理1,即對于任意 α > 0 \alpha>0 α>0,所提出算法能夠達到 α \mathcal{\alpha} α的概率的下界可計算(該下界數值詳見原文定理1)。
隨后文章通過一階和零階分析,對好事件 E ( α ) \mathcal{E}(\alpha) E(α)推導出所提出的數據驅動近似算法的樣本復雜度界限對于任意 ? > 0 \epsilon >0 ?>0且 β ∈ ( 0 , 1 ) \beta\in(0,1) β∈(0,1),若每個時期 t ∈ [ 1 , … , T ] t\in[1,\ldots,T] t∈[1,…,T]內 N t ≥ N t ( ? , β ) N_t\geq N_t(\epsilon,\beta) Nt?≥Nt?(?,β),則最優期望利潤與期望值之間(通過數據驅動策略)的利潤的絕對差距不大于 ? \epsilon ?的概率至少為 1 ? β 1-\beta 1?β,其中 N t ( T , ? , β ) = O ( T 4 ( T ? t + 1 ) 2 ? ? 2 log ? ( T / β ) . N_t(T,\epsilon,\beta)=O(T^4(T-t+1)^2\epsilon^{-2}\log(T/\beta). Nt?(T,?,β)=O(T4(T?t+1)2??2log(T/β).
該樣本復雜度界限對于 β \beta β的依賴性而言是最優的,因為其與單周期有容量限制的報童問題的信息論下界相匹配(Cheung and Simchi-Levi 2019)。 然而,對 T T T的依賴性是否緊密仍然未知,因相應的下界仍是開放的。 給定準確度水平和概率水平 β \beta β來獲得 T T T階段聯合定價和庫存控制問題的近乎最優策略,該界限可以被視為對公司所需樣本數量的保守估計。 該界限是保守的,因其為針對 η t \eta_t ηt?的所有可能的基礎分布和 Φ t \Phi_t Φt?中所有可能的基礎需求函數的最壞情況界限。
2 算法拓展
這部分的拓展主要針對前文假設的有限元素需求集,即接下來的討論以具有有界參數的(廣義)線性需求函數集為主,同時還包括算法在具有非線性報童成本的基于抽樣的庫存控制的應用。
2.1 針對廣義線性需求集的拓展
現重新定義需求集 Φ t \Phi_t Φt?如下:
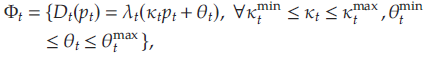
其中 λ t : R → R \lambda_t:\mathbb{R}\rightarrow\mathbb{R} λt?:R→R為由 κ t \kappa_t κt?, θ t \theta_t θt?參數化的鏈接函數,并設計矩陣
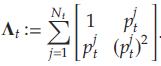
假設1:在每個時期 t ∈ [ 1 , … , T ] t\in[1,\ldots,T] t∈[1,…,T]中,隨機需求為 D t ( p t ) + η t D_t(p_t)+\eta_t Dt?(pt?)+ηt?,其中 D ( ? ) D(\cdot) D(?)是確定性需求期望函數,而 η t \eta_t ηt?是在 [ ω t min ? , ω t max ? ] [\omega_t^{\min},\omega_t^{\max}] [ωtmin?,ωtmax?]上有界的零均值連續隨機變量,且在時間上獨立。 η t \eta_t ηt?的累積分布函數是 Lipschitz 連續的,常數為 I t I_t It?.
假設 2. 在每個時期 t ∈ [ 1 , … , T ] t\in[1,\ldots,T] t∈[1,…,T]中, D t ( ? ) D_t(\cdot) Dt?(?)的反函數 D t ? 1 ( ? ) D_t^{-1}(\cdot) Dt?1?(?)是二次連續可微且嚴格遞減的,其一階導數和二階導數是有界的。此外,預期收入函數 R t ( d t ) : = d t D t ? 1 ( d t ) R_t(d_t):=d_tD_t^{-1}(d_t) Rt?(dt?):=dt?Dt?1?(dt?)在預期需求 d t d_t dt?中嚴格凹。
結合前文所述的假設1和2,現對每個時期 t ∈ [ 1 , … , T ] t\in[1,\ldots,T] t∈[1,…,T]添加新假設如下:
- 真實需求函數 D t ( ? ) D_t(\cdot) Dt?(?)為 Φ t \Phi_t Φt?中的一個廣義線性函數。
- 函數 λ t \lambda_t λt?二階可導且已知,其一階和二階導數的上界分別為 L λ t 1 L_{\lambda_t}^1 Lλt?1?和 L λ t 2 L_{\lambda_t}^2 Lλt?2?,且有 inf ? x ∈ [ κ t min ? p t min ? + θ t min ? , κ t max ? p t max ? + θ t max ? ] λ t ′ ( x ) > 0. \inf_{x\in[\kappa_t^{\min}p_t^{\min}+\theta_t^{\min},\kappa_t^{\max}p_t^{\max}+\theta_t^{\max}]}\lambda_t^{'}(x)>0. infx∈[κtmin?ptmin?+θtmin?,κtmax?ptmax?+θtmax?]?λt′?(x)>0.
- 樣本協方差矩陣的最小特征值存在通用下界 λ  ̄ t > 0 \underline{\lambda}_t>0 λ?t?>0,即矩陣 λ min ? ( 1 N t Λ t ) ≥ λ  ̄ t \lambda_{\min}(\frac{1}{N_t}\Lambda_t)\geq \underline{\lambda}_t λmin?(Nt?1?Λt?)≥λ?t?.
根據假設,至少存在兩個不同的 p t i p_t^i pti?使得矩陣 Λ t \Lambda_t Λt?可逆,

為估計參數 κ t \kappa_t κt?和 θ t \theta_t θt?, 首先找到滿足如下兩等式的 κ t ∈ R \kappa_t\in\mathbb{R} κt?∈R和 θ t ∈ R \theta_t\in\mathbb{R} θt?∈R,并將解分別投射在區間 [ κ t min ? , κ t max ? ] [\kappa_t^{\min},\kappa_t^{\max}] [κtmin?,κtmax?]和 [ θ t min ? , θ t max ? ] [\theta_t^{\min},\theta_t^{\max}] [θtmin?,θtmax?]上,進而得到 κ ^ t \hat{\kappa}_t κ^t?和 θ ^ t \hat{\theta}_t θ^t?. 于是現有的數據驅動問題中的需求可表示為 D ^ t ( p t ) = λ t ( κ ^ t p t + θ ^ t ) \hat{D}_t(p_t)=\lambda_t(\hat{\kappa}_tp_t+\hat{\theta}_t) D^t?(pt?)=λt?(κ^t?pt?+θ^t?), 經驗收益為 R ^ t ( d t ) = d t D ^ t ? 1 ( d t ) \hat{R}_t(d_t)=d_t\hat{D}_t^{-1}(d_t) R^t?(dt?)=dt?D^t?1?(dt?). 對于數據集中的每個價格-需求對,定義 η ^ t j = d t j ? D ^ t ( p t k ) = η t j ? Δ t j \hat{\eta}_t^j=d_t^j-\hat{D}_t(p_t^k)=\eta_t^j-\Delta_t^j η^?tj?=dtj??D^t?(ptk?)=ηtj??Δtj?為 η t \eta_t ηt?的偏差樣本,其中 Δ t j : = D t ( p t j ) ? D ^ t ( p t j ) \Delta_t^j:=D_t(p_t^j)-\hat{D}_t(p_t^j) Δtj?:=Dt?(ptj?)?D^t?(ptj?)為偏差項。令 E η ^ t [ f ( η ^ ) ] \mathbb{E}_{\hat{\eta}_t}[f(\hat{\eta})] Eη^?t??[f(η^?)]表示 1 N t ∑ j = 1 N t f ( η ^ t j ) \frac{1}{N_t}\sum_{j=1}^{N_t}f(\hat{\eta}_t^j) Nt?1?∑j=1Nt??f(η^?tj?), 則可定義 C ^ t ( q t ) \hat{C}_t(q_t) C^t?(qt?)如下:
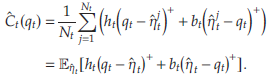
在此拓展中,文章使用基于最大似然的方法來構建經驗收益函數,并且樣本中的偏差項需要額外的集中結果。 通過原文定理5中,文章表明,樣本復雜度界限與前文所述的關于原定數據驅動問題的定理4相同。
2.2 非線性報童問題的成本函數
文章提出,若滿足以下假設7,則原文定理4和5中關于樣本復雜度界限的定理依然成立:
假設7:在每個時期 t ∈ [ 1 , … , T ] t\in[1,\ldots,T] t∈[1,…,T]中,報童問題成本函數 C t ( q t ) = E η t [ f t ( q t + η t ) ] C_t(q_t)=\mathbb{E}_{\eta_t}[f_t(q_t+\eta_t)] Ct?(qt?)=Eηt??[ft?(qt?+ηt?)], 其中 f t : R → R f_t:\mathbb{R}\rightarrow\mathbb{R} ft?:R→R為凸。對于任意 q t ∈ R q_t\in\mathbb{R} qt?∈R, 存在常數 M t C > 0 M_t^C>0 MtC?>0滿足 ∣ f t l ( q t ) ∣ ≤ M t C |f_t^l(q_t)|\leq M_t^C ∣ftl?(qt?)∣≤MtC?以及 ∣ f t r ( q t ) ∣ ≤ M t C |f_t^r(q_t)|\leq M_t^C ∣ftr?(qt?)∣≤MtC?. 同時,對于任一 q t ′ , q t ′ ′ ∈ R q_t^{'},q_t^{''}\in\mathbb{R} qt′?,qt′′?∈R, 存在常數 L t C > 0 L_t^C>0 LtC?>0滿足 ∣ f t l ( q t ′ ) ? f t l ( q t ′ ′ ) ∣ ≤ L t C ∣ q t ′ ? q t ′ ′ ∣ |f_t^l(q_t^{'})-f_t^l(q_t^{''})|\leq L_t^C|q_t^{'}-q_t^{''}| ∣ftl?(qt′?)?ftl?(qt′′?)∣≤LtC?∣qt′??qt′′?∣以及 ∣ f t r ( q t ) ′ ? f t r ( q t ′ ′ ) ∣ ≤ L t C ∣ q t ′ ? q t ′ ′ ∣ |f_t^r(q_t)^{'}-f_t^r(q_t^{''})|\leq L_t^C|q_t^{'}-q_t^{''}| ∣ftr?(qt?)′?ftr?(qt′′?)∣≤LtC?∣qt′??qt′′?∣.
假設 7 確保報童成本函數是具有有界導數和 Lipschitz 導數的凸函數的期望,但不要求函數具有任何(分段)線性結構。對于 C t ( ? ) C_t(\cdot) Ct?(?)的樣本平均近似值 C ^ t ( ? ) \hat{C}_t(\cdot) C^t?(?),構建

類似地,對導數應用樣本平均近似:

為簡化問題,文章主要針對事件 ? j = 1 , … , N t : ∣ Δ t j ∣ ≤ α / ( 2 L t C ) \forall j=1,\ldots,N_t: |\Delta_t^j|\leq \alpha/(2L_t^C) ?j=1,…,Nt?:∣Δtj?∣≤α/(2LtC?), 即偏差項的上限統一為 α / ( 2 L t C ) \alpha/(2L_t^C) α/(2LtC?),且證明(原文命題2)若對于某常數 α > 0 \alpha>0 α>0滿足 ? j = 1 , … , N t : ∣ Δ t j ∣ ≤ α / ( 2 L t C ) \forall j=1,\ldots,N_t: |\Delta_t^j|\leq \alpha/(2L_t^C) ?j=1,…,Nt?:∣Δtj?∣≤α/(2LtC?),則
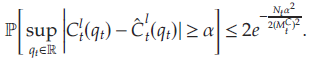
2.3 計算復雜度的降低
文章分析,所提出的DDPIC算法存在一個計算復雜性的問題是,通過 SAA 方法構建的數據驅動動態規劃中的函數可能在 T T T中具有指數數量的斷點。這個問題可通過運用 Cheung 和 Simchi-Levi(2019 )提出的稀疏化方法,提供多項式時間近似算法來求解數據驅動的動態規劃。 雖然多項式時間算法比沒有稀疏化的 SAA 方法需要更多的樣本,但它們的樣本復雜度在 T T T, ? \epsilon ?, β \beta β 中相同。 關鍵的改進是,通過稀疏化技術,算法只需要在多項式斷點處評估值函數的導數。
稀疏化的思想是在通過后向歸納法求解動態規劃時,通過每個周期的導數重采樣步驟來減少 V t ( x t ) V_t(x_t) Vt?(xt?)的斷點數量。 此步驟在以下算法中for循環的最后兩行中進行了說明:

文章指出,稀疏化算法對 N 1 , ? , N T , T , 1 ζ N_1, \cdots,N_T,T, \frac{1}{\zeta} N1?,?,NT?,T,ζ1?具有多項式運行時間,其中稀疏系數 ζ \zeta ζ控制了運行時間復雜度和樣本復雜度的平衡。特別地,若令 ζ : = α 1 \zeta:=\alpha_1 ζ:=α1?(與定理4和5中的標量相同),則算法仍具有樣本復雜度 O ( T 6 ? ? 2 log ? ( T / β ) O(T^6\epsilon^{-2}\log(T/\beta) O(T6??2log(T/β).
3 數值實驗
3.1 實驗設置
- 實驗問題
考慮 T = 7 T=7 T=7個時期、起始庫存為 x x x,其中 x x x由均勻分布 X ~ [ 0 , 80 ] X\sim[0,80] X~[0,80]取樣。在每個時期 t ∈ { 1 , … , T } t\in\{1,\ldots,T\} t∈{1,…,T}中,令可行價格區間為 [ p t min ? , p t max ? ] = [ 60 , 90 ] [p_t^{\min},p_t^{\max}]=[60,90] [ptmin?,ptmax?]=[60,90]以及單位訂貨成本 c t = 60 c_t=60 ct?=60. 需求函數 D t ( ? ) D_t(\cdot) Dt?(?)有以下三個參數族函數之一:(具體的參數數值請參考原文章節6.1.1)
a. 線性需求: D t ( p ) = κ t + θ t p D_t(p)=\kappa_t+\theta_tp Dt?(p)=κt?+θt?p( t = 3 , … , 7 t=3,\ldots,7 t=3,…,7);
b. 指數需求: D t ( p ) = e κ t + θ t p D_t(p)=e^{\kappa_t+\theta_tp} Dt?(p)=eκt?+θt?p ( t = 1 t=1 t=1);
c. 對數需求: D t ( p ) = M D ? e κ t + θ t p / ( 1 + e κ t + θ t p ) , M D = 600 D_t(p)=M_D\cdot e^{\kappa_t+\theta_tp}/(1+e^{\kappa_t+\theta_tp}), M_D=600 Dt?(p)=MD??eκt?+θt?p/(1+eκt?+θt?p),MD?=600 ( t = 2 t=2 t=2).
隨機噪聲 η t \eta_t ηt?的分布由以下兩族選擇:
a. 均勻分布: Unif ( ? ω t , ω t ) ; \text{Unif}(-\omega_t,\omega_t); Unif(?ωt?,ωt?);
b. 截斷正態分布: Normal ( 0 , σ t ) \text{Normal}(0,\sigma_t) Normal(0,σt?), 只取 [ ? ω t , ω t ] [-\omega_t,\omega_t] [?ωt?,ωt?]范圍內的值。
依照上述設定,構建數據驅動問題,對價格-需求對取樣,其中對價格在 [ p t min ? , p t max ? ] [p_t^{\min},p_t^{\max}] [ptmin?,ptmax?]中取樣,并設定 N t ∈ { 20 , ? , 160 } N_t\in\{20,\cdots,160\} Nt?∈{20,?,160}.
- 算法表現衡量標準
令 μ = { μ 1 , … , μ T } \mu=\{\mu_1,\ldots,\mu_T\} μ={μ1?,…,μT?}為針對 T T T與 x x x的任意庫存策略,其期望收益為 π 1 ( x ; μ ) \pi_1(x;\mu) π1?(x;μ),使其達到最優的收益 π 1 ( x ; μ ? ) \pi_1(x;\mu^*) π1?(x;μ?)的策略 μ ? = { μ 1 ? , … , μ T ? } \mu^*=\{\mu_1^*,\ldots,\mu_T^*\} μ?={μ1??,…,μT??}為最優策略。文章運用絕對最有差距 (absolute optimality gap), π ( μ ? ) ? π ( μ ) \pi(\mu^*)-\pi(\mu) π(μ?)?π(μ), 來衡量任意策略與最優策略的期望收益差距,該數值越小則策略越優。
- 基準算法
對于全信息問題,文章引用Bernstein et al. (2016) 中提出的啟發式算法作為基準算法 (Heuristic-FI)。該算法計算短視需求函數 (myopic demand) 作為定價/需求設定策略,并遵循基本庫存策略 (base-stock policy)來做出庫存補貨決策。原算法中設定交貨時間 (lead time)為正,為符合模型設定,文章化用該算法,細節詳見章節6.1.3.
對于數據驅動問題,文章將由DDPIC 所得的收益和成本函數代入 Heuristic-FI 來確定定價和補貨決策。該算法被記作 Heuristic-DD.
3.2 構建需求假設集
給定 N t N_t Nt?個價格-需求對樣本 { p t j , d t j } \{p_t^j,d_t^j\} {ptj?,dtj?},文章為需求假設集 Φ t \Phi_t Φt?構建 K t K_t Kt?個候選需求函數。具體來說,對每個需求函數族:
- 根據數據估計價格敏感度參數 θ t \theta_t θt?的下限 θ ^ t min ? \hat{\theta}_t^{\min} θ^tmin?和上限 θ ^ t max ? \hat{\theta}_t^{\max} θ^tmax?;
- 在 θ ^ t min ? \hat{\theta}_t^{\min} θ^tmin?與 θ ^ t max ? \hat{\theta}_t^{\max} θ^tmax?之間取5個均勻分布的數值 { θ t ( 1 ) , ? , θ t ( 5 ) } \{\theta_t^{(1)},\cdots,\theta_t^{(5)}\} {θt(1)?,?,θt(5)?};
- 利用5組 κ t ( k ) \kappa_t^{(k)} κt(k)?和 θ t ( k ) \theta_t^{(k)} θt(k)?,構建5個需求函數,其中 κ t ( k ) \kappa_t^{(k)} κt(k)?為能最小化給定 θ t ( k ) ∈ { θ t ( 1 ) , ? , θ t ( 5 ) } \theta_t^{(k)}\in\{\theta_t^{(1)},\cdots,\theta_t^{(5)}\} θt(k)?∈{θt(1)?,?,θt(5)?}經驗平方誤差的參數。
由于底層需求函數族未知,文章從這三個族中收集候選需求函數,總共 K t = 15 K_t=15 Kt?=15個函數,形成需求假設集 Φ t \Phi_t Φt?(見圖 1)。 最后,文章將 Φ t \Phi_t Φt?輸入到DDPIC算法中,以計算數據驅動的定價和庫存補貨政策。

3.3 算法表現比較
文章在圖2比較了Heuristic-FI、Heuristic-DD 和 DDPIC 與最優收益 π ( μ ? ) \pi(\mu^*) π(μ?)的絕對最優性差距。 可以看到,隨著數據大小 N N N的增長,最優性差距在所提出的算法 DDPIC 和基準算法 Heuristic-DD 都有所提高(因需求學習和 SAA 過程隨著樣本的增多而變得更加準確),而Heuristic-FI 是在全信息環境下實現的,因此其收益差距與樣本大小無關。 在所有三種算法中,DDPIC 在 N ≥ 40 N\geq 40 N≥40時實現最佳性能,并且在該問題設置中,當 n = 20 n=20 n=20時,它能夠將絕對利潤差距保持在 114.30 以下;當 n = 160 n=160 n=160時,它能夠將絕對利潤差距保持在 15.79 以下,即相對差距分別為 < 7.68 % <7.68\% <7.68% 和 < 1.06 % <1.06\% <1.06%.
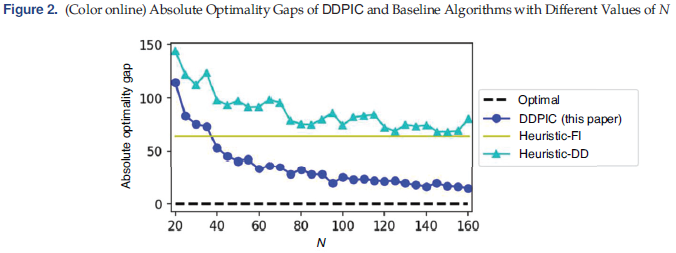
由于 Heuristic-FI 和 Heuristic-DD 中的啟發式設計使用短視需求函數,因此這兩種基準算法并不總是表現得良好。 當庫存水平 y y y值很大時,算法的性能通常會下降,此時最優需求函數不能通過啟發式逼近,從而導致初始庫存平均預期利潤差距比 DDPIC 更大。 另一方面,所提出的算法DDPIC通過逆向歸納法構造經驗動態規劃并計算經驗解,隨著樣本量 N N N越大,經驗需求函數和噪聲分布變得更加準確,其性能得以不斷提高。但是,當 N N N較小時, DDPIC 沒有足夠的信息來生成類似 Heuristic-FI 接近最優的策略,因為文章假設后者擁有完整的信息。 總體而言,在文章的問題設置中,當 N N N較大時,DDPIC 能夠將兩種基準算法的利潤差距縮小到 > 85 % >85\% >85%. 當 N N N很小時,Heuristic-FI 的性能可能優于 DDPIC.
3.4 問題設置的影響
文章隨后研究了不同程度的報童成本和噪聲方差對 DDPIC 和基準算法性能的影響。
首先引入報童成本比例因子 λ c o s t \lambda_{cost} λcost?,即持有成本 h t h_t ht?和積壓成本 b t b_t bt?的乘數。 該比例因子影響報童成本與收益之比的大小,因此控制了聯合定價和庫存控制問題中管理庫存的相對“重要性”。表1顯示,隨著 λ c o s t \lambda_{cost} λcost?的增加,兩種數據驅動算法(Heuristic-DD、DDPIC)的利潤差距變得更大,因報童對任何供需不匹配的成本“懲罰”都會放大。 然而,當 λ c o s t \lambda_{cost} λcost?變化時,Heuristic-FI 的性能要穩定得多,因該算法準確地學習了最佳基礎庫存水平。 此外,文章發現所提出的算法 DDPIC 的最優性差距比兩種基準算法的值小得多,因其目標是準確地逼近真實的動態規劃,并且比其他基于啟發式的算法更不易受到成本放大的影響。 所以當 λ c o s t \lambda_{cost} λcost?從 0.5 增加到 1.5 時,DDPIC 相對于基準算法 Heuristic-FI 和 Heuristic-DD 的收益差距從 32% 左右改善到 61% 以上。

其次,文章通過使用 η t ′ = λ c o s t η t \eta_t^{'}=\lambda_{cost}\eta_t ηt′?=λcost?ηt?來改變噪聲的方差,其中 η t \eta_t ηt?為噪聲隨機變量, λ n o i s e \lambda_{noise} λnoise?是噪聲縮放因子。給定相同數量的樣本,噪聲縮放因子 λ n o i s e \lambda_{noise} λnoise?會影響學習任務的“難度”,因為具有較大噪聲的需求樣本使得需求函數和噪聲分布的估計更具挑戰性。 表2證實了所提出的數據驅動算法DDPIC以最小的 λ \lambda λ噪聲值獲得了最佳性能,在此情況下算法的收益差距小于16,相當于相對最優性差距<1%。 在所有實驗中,DDPIC 都能夠將基準算法的收益差距縮小 40% 以上。

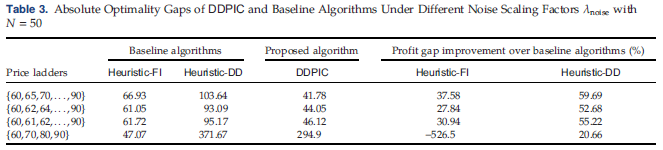
最后,文章通過實證檢驗了價格階梯對所提出算法性能的影響。文章通過搜索離散價格中的最佳價格來修改所提出的算法,并計算每組離散價格的利潤差距。 表3顯示,當可行價格稀疏時,如只有四個離散可行價格{60,70,80,90}的情況所示,所提出算法的修改版本的利潤差距明顯更大。 同時,Heuristic-FI 保持了特別小的最優性差距,因此價格階梯的稀疏性導致兩種數據驅動算法對真實需求模型的學習不足。 此外,文章指出, DDPIC算法是為連續定價決策而設計的,因此可能存在更好的數據驅動聯合定價和庫存控制算法,專門為價格階梯設計。 當離散價格集合較密集時,算法的性能與連續價格區間的原始問題設置相似,并且 DDPIC 能夠
4 結論
- 文章聚焦于數據驅動的聯合定價和庫存控制問題的樣本復雜度界限,證明了該問題相較于一般多階段隨機規劃問題的指數樣本復雜度界限,具有多項式樣本復雜度界限,使得數據驅動解決方案更為可行。
- 文章提出了一種樣本高效算法,并證明其在合理數據量下生成接近最優的定價和庫存策略的有效性,凸顯了理論發現的實際應用性。
- 未來研究方向包括將分析擴展到非參數需求函數、解決乘法需求模型和帶需求審查的缺貨模型的挑戰,以及探索改進 O ~ ( T 6 ) \tilde{O}(T^6) O~(T6)樣本復雜度界限以提高效率。
參考文獻
Chen X, Simchi-Levi D (2004) Coordinating inventory control and pricing strategies with random demand and fixed ordering cost: The finite horizon case. Oper. Res. 52(6):887–896.
Cheung WC, Simchi-Levi D (2019) Sampling-based approximation schemes for capacitated stochastic inventory control models. Math. Oper. Res. 44(2):668–692.
Negahban S, Wainwright MJ (2011) Estimation of (near) low-rank matrices with noise and high-dimensional scaling. Ann. Statist. 39(2):1069–1097.
Bernstein F, Li Y, Shang K (2016) A simple heuristic for joint inventory and pricing models with lead time and backorders. Management Sci. 62(8):2358–2373.



有案例!)
)






)







