一、問題

0.1 + 0.2 === 0.3 // false

二、浮點數

“浮點數”是一種表示數字的標準，整數也可以用浮點數的格式來存儲

我們也可以理解成，浮點數就是小數

在JavaScript中，現在主流的數值類型是Number，而Number采用的是IEEE754規范中64位雙精度浮點數編碼

這樣的存儲結構優點是可以歸一化處理整數和小數，節省存儲空間

對于一個整數，可以很輕易轉化成十進制或者二進制。但是對于一個浮點數來說，因為小數點的存在，小數點的位置不是固定的。解決思路就是使用科學計數法，這樣小數點位置就固定了

而計算機只能用二進制（0或1）表示，二進制轉換為科學記數法的公式如下：

其中，a的值為0或者1，e為小數點移動的位置

舉個例子：

27.0轉化成二進制為11011.0 ，科學計數法表示為：

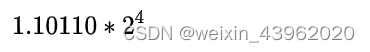
前面講到，javaScript存儲方式是雙精度浮點數，其長度為8個字節，即64位比特

64位比特又可分為三個部分：

• 符號位S：第 1 位是正負數符號位（sign），0代表正數，1代表負數
• 指數位E：中間的 11 位存儲指數（exponent），用來表示次方數，可以為正負數。在雙精度浮點數中，指數的固定偏移量為1023
• 尾數位M：最后的 52 位是尾數（mantissa），超出的部分自動進一舍零

三、問題分析

在javascript語言中，0.1 和 0.2 都轉化成二進制后再進行運算

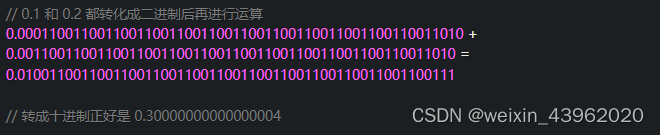
所以輸出false

再來一個問題，那么為什么x=0.1得到0.1？

主要是存儲二進制時小數點的偏移量最大為52位，最多可以表達的位數是2^53=9007199254740992，對應科學計數尾數是?9.007199254740992，這也是 JS 最多能表示的精度

它的長度是 16，所以可以使用?toPrecision(16)?來做精度運算，超過的精度會自動做湊整處理

但看到的?0.1?實際上并不是?0.1。用更高的精度試試：

四、結論

計算機存儲雙精度浮點數需要先把十進制數轉換為二進制的科學記數法的形式，然后計算機以自己的規則{符號位+(指數位+指數偏移量的二進制)+小數部分}存儲二進制的科學記數法

因為存儲時有位數限制（64位），并且某些十進制的浮點數在轉換為二進制數時會出現無限循環，會造成二進制的舍入操作(0舍1入)，當再轉換為十進制時就造成了計算誤差