647. 回文子串

力扣題目鏈接(opens new window)

給定一個字符串，你的任務是計算這個字符串中有多少個回文子串。

具有不同開始位置或結束位置的子串，即使是由相同的字符組成，也會被視作不同的子串。

示例 1：

• 輸入："abc"
• 輸出：3
• 解釋：三個回文子串: "a", "b", "c"

示例 2：

• 輸入："aaa"
• 輸出：6
• 解釋：6個回文子串: "a", "a", "a", "aa", "aa", "aaa"

提示：輸入的字符串長度不會超過 1000 。

#思路

#暴力解法

兩層for循環，遍歷區間起始位置和終止位置，然后還需要一層遍歷判斷這個區間是不是回文。所以時間復雜度：O(n^3)

#動態規劃

動規五部曲：

1. 確定dp數組（dp table）以及下標的含義

如果大家做了很多這種子序列相關的題目，在定義dp數組的時候 很自然就會想題目求什么，我們就如何定義dp數組。

絕大多數題目確實是這樣，不過本題如果我們定義，dp[i] 為 下標i結尾的字符串有 dp[i]個回文串的話，我們會發現很難找到遞歸關系。

dp[i] 和 dp[i-1] ，dp[i + 1] 看上去都沒啥關系。

所以我們要看回文串的性質。 如圖：

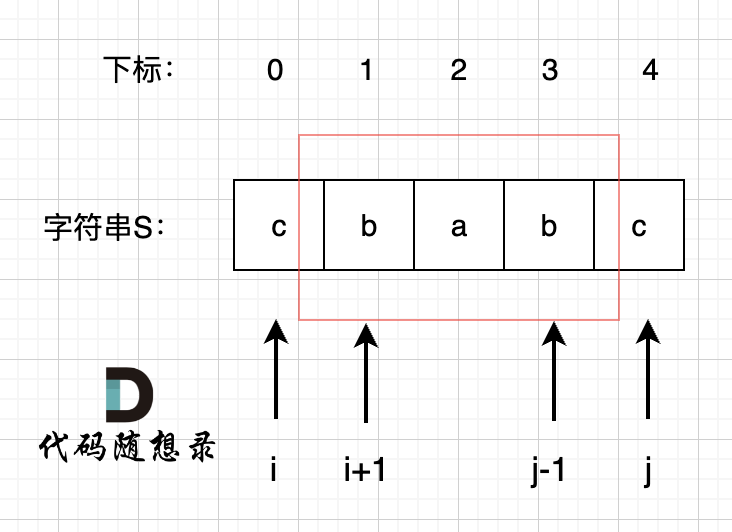
我們在判斷字符串S是否是回文，那么如果我們知道 s[1]，s[2]，s[3] 這個子串是回文的，那么只需要比較 s[0]和s[4]這兩個元素是否相同，如果相同的話，這個字符串s 就是回文串。

那么此時我們是不是能找到一種遞歸關系，也就是判斷一個子字符串（字符串的下表范圍[i,j]）是否回文，依賴于，子字符串（下表范圍[i + 1, j - 1]）） 是否是回文。

所以為了明確這種遞歸關系，我們的dp數組是要定義成一位二維dp數組。

布爾類型的dp[i][j]：表示區間范圍[i,j] （注意是左閉右閉）的子串是否是回文子串，如果是dp[i][j]為true，否則為false。

1. 確定遞推公式

在確定遞推公式時，就要分析如下幾種情況。

整體上是兩種，就是s[i]與s[j]相等，s[i]與s[j]不相等這兩種。

當s[i]與s[j]不相等，那沒啥好說的了，dp[i][j]一定是false。

當s[i]與s[j]相等時，這就復雜一些了，有如下三種情況

• 情況一：下標i 與 j相同，同一個字符例如a，當然是回文子串
• 情況二：下標i 與 j相差為1，例如aa，也是回文子串
• 情況三：下標：i 與 j相差大于1的時候，例如cabac，此時s[i]與s[j]已經相同了，我們看i到j區間是不是回文子串就看aba是不是回文就可以了，那么aba的區間就是 i+1 與 j-1區間，這個區間是不是回文就看dp[i + 1][j - 1]是否為true。

以上三種情況分析完了，那么遞歸公式如下：

if (s[i] == s[j]) {if (j - i <= 1) { // 情況一 和 情況二result++;dp[i][j] = true;} else if (dp[i + 1][j - 1]) { // 情況三result++;dp[i][j] = true;}
}

result就是統計回文子串的數量。

注意這里我沒有列出當s[i]與s[j]不相等的時候，因為在下面dp[i][j]初始化的時候，就初始為false。

1. dp數組如何初始化

dp[i][j]可以初始化為true么？ 當然不行，怎能剛開始就全都匹配上了。

所以dp[i][j]初始化為false。

1. 確定遍歷順序

遍歷順序可有有點講究了。

首先從遞推公式中可以看出，情況三是根據dp[i + 1][j - 1]是否為true，在對dp[i][j]進行賦值true的。

dp[i + 1][j - 1] 在 dp[i][j]的左下角，如圖：

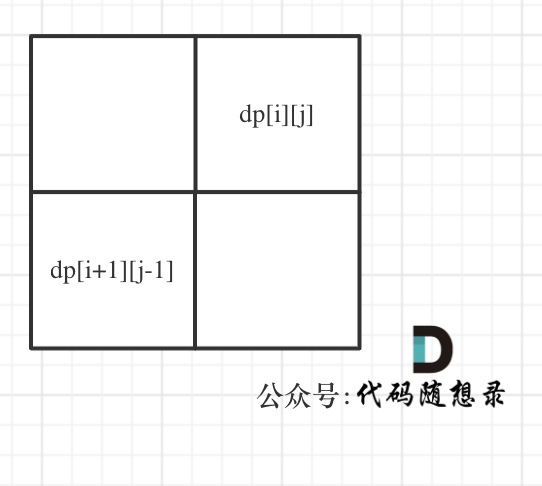
如果這矩陣是從上到下，從左到右遍歷，那么會用到沒有計算過的dp[i + 1][j - 1]，也就是根據不確定是不是回文的區間[i+1,j-1]，來判斷了[i,j]是不是回文，那結果一定是不對的。

所以一定要從下到上，從左到右遍歷，這樣保證dp[i + 1][j - 1]都是經過計算的。

有的代碼實現是優先遍歷列，然后遍歷行，其實也是一個道理，都是為了保證dp[i + 1][j - 1]都是經過計算的。

代碼如下：

for (int i = s.size() - 1; i >= 0; i--) {  // 注意遍歷順序for (int j = i; j < s.size(); j++) {if (s[i] == s[j]) {if (j - i <= 1) { // 情況一 和 情況二result++;dp[i][j] = true;} else if (dp[i + 1][j - 1]) { // 情況三result++;dp[i][j] = true;}}}
}

1. 舉例推導dp數組

舉例，輸入："aaa"，dp[i][j]狀態如下：

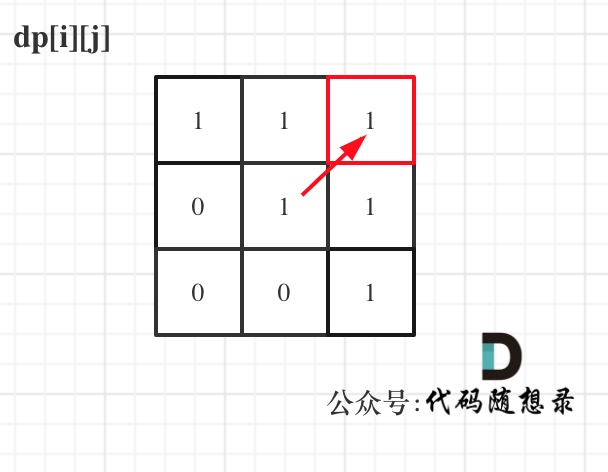
圖中有6個true，所以就是有6個回文子串。

注意因為dp[i][j]的定義，所以j一定是大于等于i的，那么在填充dp[i][j]的時候一定是只填充右上半部分。

以上分析完畢，C++代碼如下：

class Solution {
public:int countSubstrings(string s) {vector<vector<bool>> dp(s.size(), vector<bool>(s.size(), false));int result = 0;for (int i = s.size() - 1; i >= 0; i--) {  // 注意遍歷順序for (int j = i; j < s.size(); j++) {if (s[i] == s[j]) {if (j - i <= 1) { // 情況一 和 情況二result++;dp[i][j] = true;} else if (dp[i + 1][j - 1]) { // 情況三result++;dp[i][j] = true;}}}}return result;}
};

以上代碼是為了凸顯情況一二三，當然是可以簡潔一下的，如下：

class Solution {
public:int countSubstrings(string s) {vector<vector<bool>> dp(s.size(), vector<bool>(s.size(), false));int result = 0;for (int i = s.size() - 1; i >= 0; i--) {for (int j = i; j < s.size(); j++) {if (s[i] == s[j] && (j - i <= 1 || dp[i + 1][j - 1])) {result++;dp[i][j] = true;}}}return result;}
};

• 時間復雜度：O(n^2)
• 空間復雜度：O(n^2)

#雙指針法

動態規劃的空間復雜度是偏高的，我們再看一下雙指針法。

首先確定回文串，就是找中心然后向兩邊擴散看是不是對稱的就可以了。

在遍歷中心點的時候，要注意中心點有兩種情況。

一個元素可以作為中心點，兩個元素也可以作為中心點。

那么有人同學問了，三個元素還可以做中心點呢。其實三個元素就可以由一個元素左右添加元素得到，四個元素則可以由兩個元素左右添加元素得到。

所以我們在計算的時候，要注意一個元素為中心點和兩個元素為中心點的情況。

這兩種情況可以放在一起計算，但分別計算思路更清晰，我傾向于分別計算，代碼如下：

class Solution {
public:int countSubstrings(string s) {int result = 0;for (int i = 0; i < s.size(); i++) {result += extend(s, i, i, s.size()); // 以i為中心result += extend(s, i, i + 1, s.size()); // 以i和i+1為中心}return result;}int extend(const string& s, int i, int j, int n) {int res = 0;while (i >= 0 && j < n && s[i] == s[j]) {i--;j++;res++;}return res;}
};

• 時間復雜度：O(n^2)
• 空間復雜度：O(1)

?

516.最長回文子序列

力扣題目鏈接(opens new window)

給定一個字符串 s ，找到其中最長的回文子序列，并返回該序列的長度。可以假設 s 的最大長度為 1000 。

示例 1: 輸入: "bbbab" 輸出: 4 一個可能的最長回文子序列為 "bbbb"。

示例 2: 輸入:"cbbd" 輸出: 2 一個可能的最長回文子序列為 "bb"。

提示：

• 1 <= s.length <= 1000
• s 只包含小寫英文字母

#思路

我們剛剛做過了?動態規劃：回文子串?(opens new window)，求的是回文子串，而本題要求的是回文子序列， 要搞清楚這兩者之間的區別。

回文子串是要連續的，回文子序列可不是連續的！?回文子串，回文子序列都是動態規劃經典題目。

回文子串，可以做這兩題：

• 647.回文子串
• 5.最長回文子串

思路其實是差不多的，但本題要比求回文子串簡單一點，因為情況少了一點。

動規五部曲分析如下：

1. 確定dp數組（dp table）以及下標的含義

dp[i][j]：字符串s在[i, j]范圍內最長的回文子序列的長度為dp[i][j]。

1. 確定遞推公式

在判斷回文子串的題目中，關鍵邏輯就是看s[i]與s[j]是否相同。

如果s[i]與s[j]相同，那么dp[i][j] = dp[i + 1][j - 1] + 2;

如圖：?

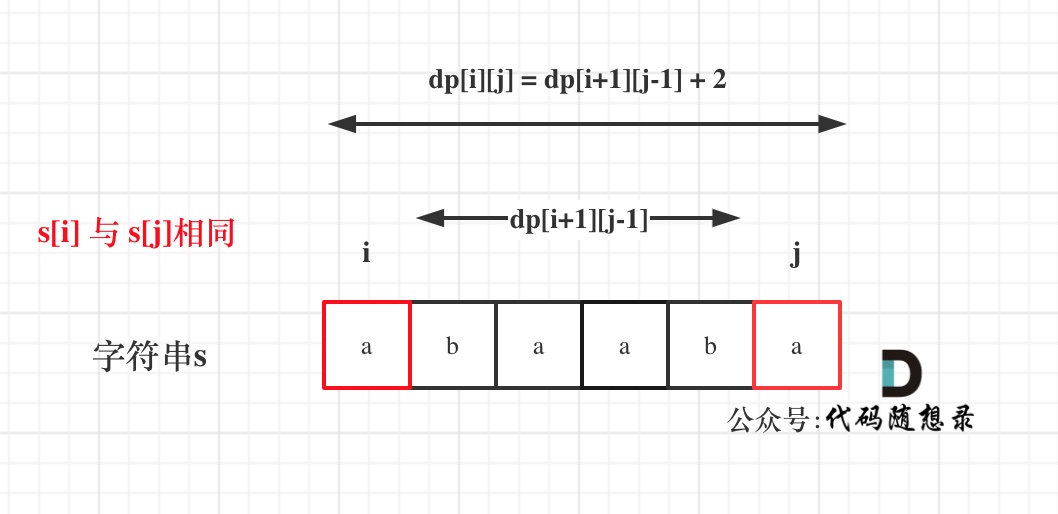
（如果這里看不懂，回憶一下dp[i][j]的定義）

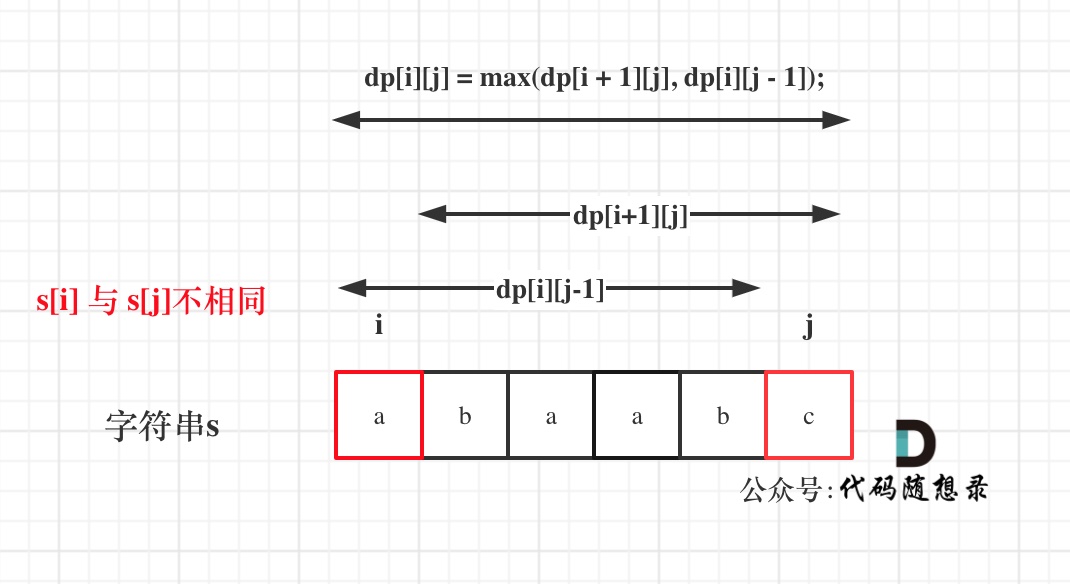
如果s[i]與s[j]不相同，說明s[i]和s[j]的同時加入 并不能增加[i,j]區間回文子序列的長度，那么分別加入s[i]、s[j]看看哪一個可以組成最長的回文子序列。

加入s[j]的回文子序列長度為dp[i + 1][j]。

加入s[i]的回文子序列長度為dp[i][j - 1]。

那么dp[i][j]一定是取最大的，即：dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);

代碼如下：

if (s[i] == s[j]) {dp[i][j] = dp[i + 1][j - 1] + 2;
} else {dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);
}

1. dp數組如何初始化

首先要考慮當i 和j 相同的情況，從遞推公式：dp[i][j] = dp[i + 1][j - 1] + 2; 可以看出 遞推公式是計算不到 i 和j相同時候的情況。

所以需要手動初始化一下，當i與j相同，那么dp[i][j]一定是等于1的，即：一個字符的回文子序列長度就是1。

其他情況dp[i][j]初始為0就行，這樣遞推公式：dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]); 中dp[i][j]才不會被初始值覆蓋。

vector<vector<int>> dp(s.size(), vector<int>(s.size(), 0));
for (int i = 0; i < s.size(); i++) dp[i][i] = 1;

1. 確定遍歷順序

從遞歸公式中，可以看出，dp[i][j] 依賴于 dp[i + 1][j - 1] ，dp[i + 1][j] 和 dp[i][j - 1]，如圖：

所以遍歷i的時候一定要從下到上遍歷，這樣才能保證下一行的數據是經過計算的。

j的話，可以正常從左向右遍歷。

代碼如下：

for (int i = s.size() - 1; i >= 0; i--) {for (int j = i + 1; j < s.size(); j++) {if (s[i] == s[j]) {dp[i][j] = dp[i + 1][j - 1] + 2;} else {dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);}}
}

1. 舉例推導dp數組

輸入s:"cbbd" 為例，dp數組狀態如圖：

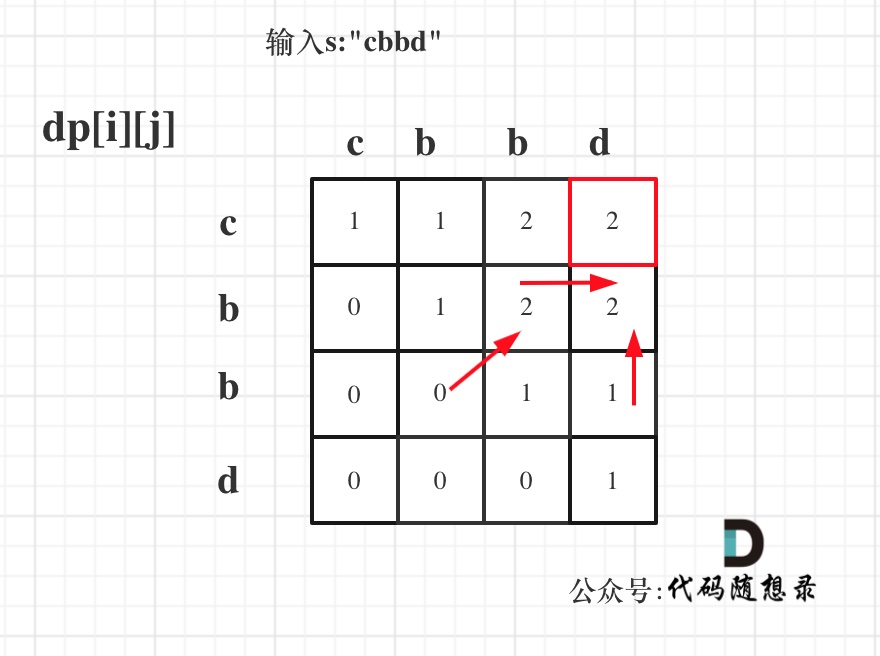
紅色框即：dp[0][s.size() - 1]; 為最終結果。

以上分析完畢，C++代碼如下：

class Solution {
public:int longestPalindromeSubseq(string s) {vector<vector<int>> dp(s.size(), vector<int>(s.size(), 0));for (int i = 0; i < s.size(); i++) dp[i][i] = 1;for (int i = s.size() - 1; i >= 0; i--) {for (int j = i + 1; j < s.size(); j++) {if (s[i] == s[j]) {dp[i][j] = dp[i + 1][j - 1] + 2;} else {dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);}}}return dp[0][s.size() - 1];}
};

• 時間復雜度: O(n^2)
• 空間復雜度: O(n^2)