平衡樹、二叉樹、靈活應用中序遍歷（值大小有序）

669. 修剪二叉搜索樹

給你二叉搜索樹的根節點 root ，同時給定最小邊界low 和最大邊界 high。通過修剪二叉搜索樹，使得所有節點的值在[low, high]中。修剪樹 不應該 改變保留在樹中的元素的相對結構 (即，如果沒有被移除，原有的父代子代關系都應當保留)。

發現規律：
二叉搜索樹特性：左子樹均小于根節點，右子樹均大于根節點,所以若值不在區間則只需要保留其中一條子樹；否則正常遍歷處理

class Solution {
public:
//二叉搜索樹特性：左子樹均小于根節點，右子樹均大于根節點,所以若值不在區間則只需要保留其中一條子樹TreeNode* trimBST(TreeNode* root, int low, int high) {if(root == nullptr) return nullptr;if(root->val > high) {return trimBST(root->left, low, high);}else if(root->val < low) {return trimBST(root->right, low, high);}root->left = trimBST(root->left, low, high);root->right = trimBST(root->right, low, high);return root;}
};

108.將有序數組轉換為二叉搜索樹

給你一個整數數組 nums ，其中元素已經按 升序 排列，請你將其轉換為一棵 高度平衡 二叉搜索樹。
高度平衡 二叉樹是一棵滿足「每個節點的左右兩個子樹的高度差的絕對值不超過 1 」的二叉樹。

思路： 為使平衡，則取升序序列中間值為分割點（根節點），以分割點為界，左序列為左子樹，右序列為右子樹

class Solution {
public:
//平衡二叉搜索樹，即二叉搜索樹中每個節點的左右子樹高度差絕對值相差不會超過1
//為使平衡，則取升序序列中間值為分割點（根節點）TreeNode* ArrayToBst(vector<int>& nums, int left, int right){if(left > right) return nullptr;TreeNode* root = new TreeNode();int mid = left + (right - left)/2;root->val = nums[mid];root->left = ArrayToBst(nums, left, mid-1);root->right = ArrayToBst(nums, mid+1, right);return root;}TreeNode* sortedArrayToBST(vector<int>& nums) {if(nums.empty()) return nullptr;return ArrayToBst(nums, 0, nums.size()-1);}
};

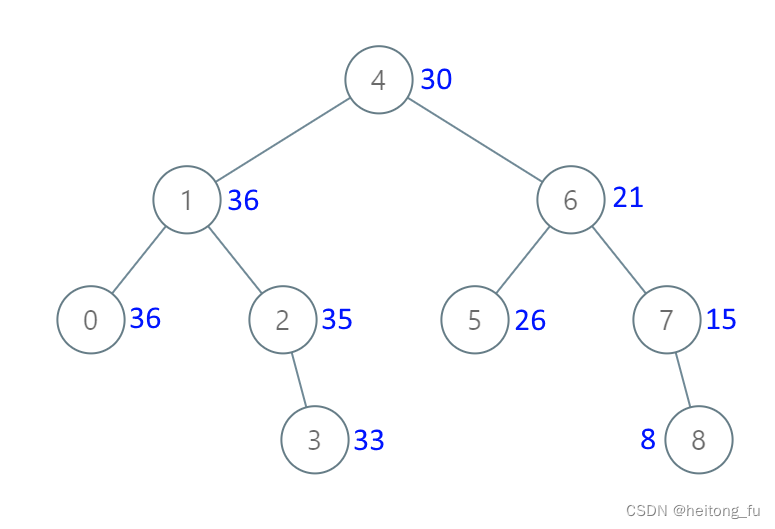
538.把二叉搜索樹轉換為累加樹

思路：
從示例1可以看出 累加樹逆中序（與正常中序不同，先訪問右節點，后訪問左節點）的節點值為降序累加序列

class Solution {
public:
//從示例1可以看出 累加樹逆中序（與正常中序不同，先訪問右節點，后訪問左節點）的節點值為降序累加序列TreeNode* ToSumTree(TreeNode* root, int &num){if(root == nullptr) return nullptr;root->right = ToSumTree(root->right, num);num += root->val; //中序遍歷保證訪問序列值有序root->val = num;root-> left = ToSumTree(root->left, num);return root;}TreeNode* convertBST(TreeNode* root) {int num = 0;return ToSumTree(root, num);}
};