343. 整數拆分

題目鏈接：整數拆分

題目描述：
給定一個正整數 n ，將其拆分為 k 個 正整數 的和（ k >= 2 ），并使這些整數的乘積最大化。
返回 你可以獲得的最大乘積 。

解題思路：
1、確定dp數組（dp table）以及下標的含義
設置dp[i] 為i的拆分最大值
2、確定遞推公式
dp[i] = max(dp[i], max((i - j) * j, dp[i - j] *j));
前一部分為將i分為i-j和j兩部分，后一部分是將i分為j和更多的分塊的i-j。
3、dp數組如何初始化
按照定義可以知道只有dp[2]有意義為1
4、確定遍歷順序
dp[i] 是依靠 dp[i - j]的狀態，所以遍歷i一定是從前向后遍歷，先有dp[i - j]再有dp[i]。
5、舉例推導dp數組

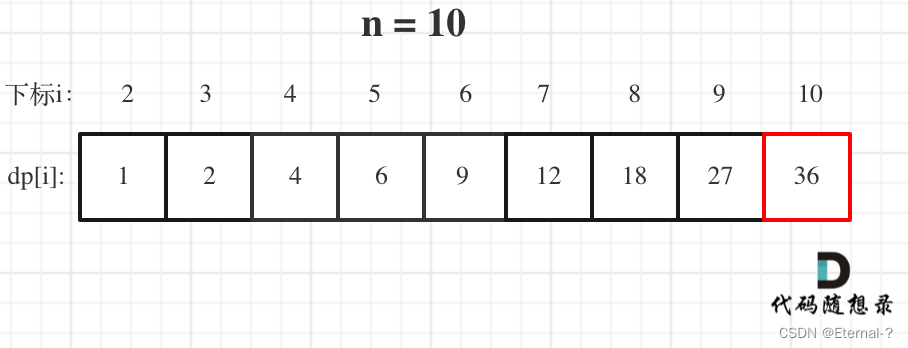
代碼實現：

class Solution {public int integerBreak(int n) {int[] dp = new int[n+1];dp[2] = 1;for(int i = 3;i<=n;i++){for(int j = 1; j<=i-j;j++){dp[i] = Math.max(dp[i],Math.max(j*(i-j),j*dp[i-j]));System.out.println(dp[i]);}}return dp[n];}
}

96. 不同的二叉搜索樹

題目鏈接：不同的二叉搜索樹

題目描述：
給你一個整數 n ，求恰由 n 個節點組成且節點值從 1 到 n 互不相同的 二叉搜索樹 有多少種？返回滿足題意的二叉搜索樹的種數。

解題思路：
本題主要的難點在于遞推過程的理解，借用卡哥的解釋

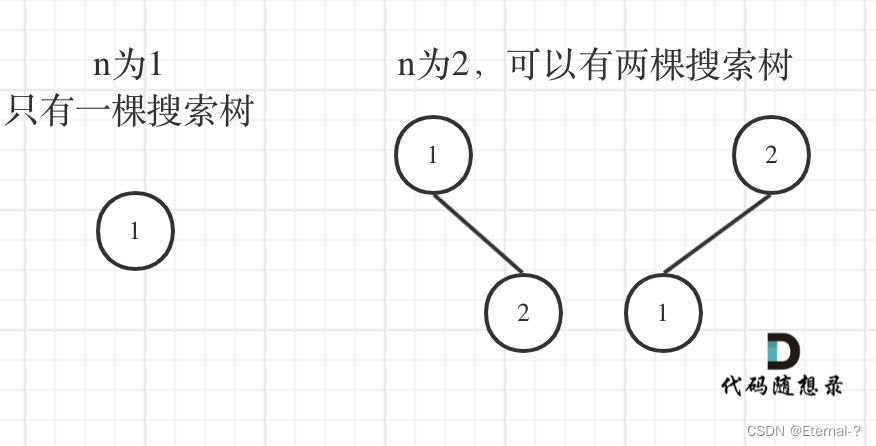
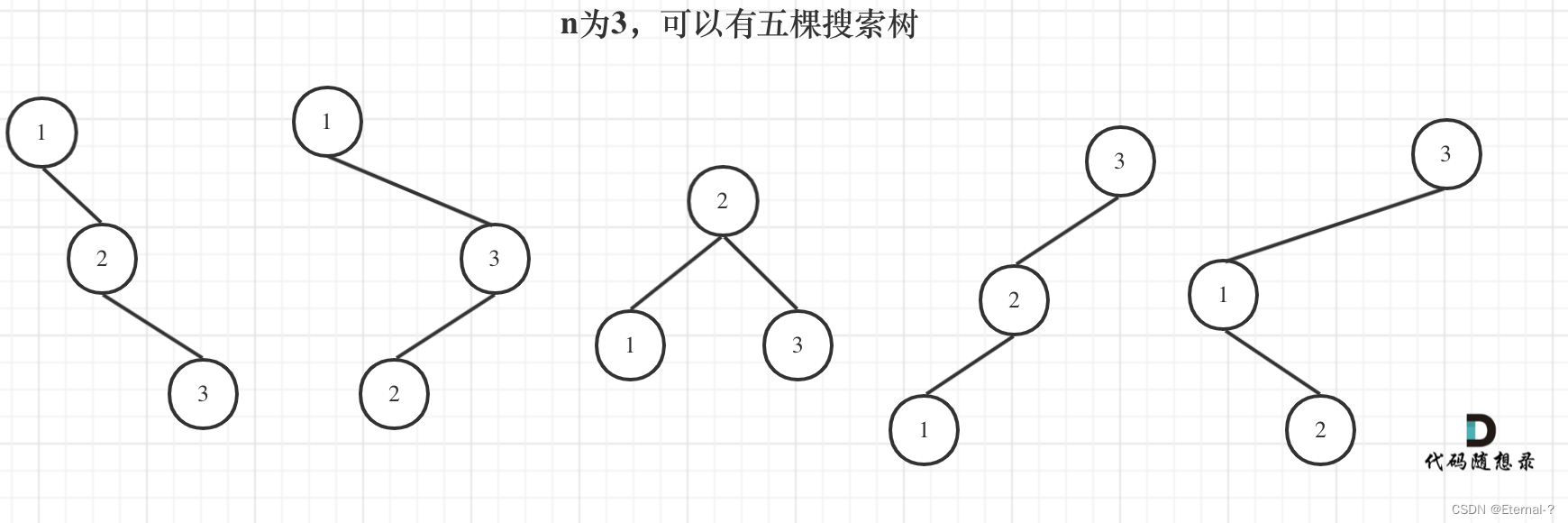
當1為頭結點的時候，其右子樹有兩個節點，看這兩個節點的布局，是不是和 n 為2的時候兩棵樹的布局是一樣的啊！
（可能有同學問了，這布局不一樣啊，節點數值都不一樣。別忘了我們就是求不同樹的數量，并不用把搜索樹都列出來，所以不用關心其具體數值的差異）
當3為頭結點的時候，其左子樹有兩個節點，看這兩個節點的布局，是不是和n為2的時候兩棵樹的布局也是一樣的啊！
當2為頭結點的時候，其左右子樹都只有一個節點，布局是不是和n為1的時候只有一棵樹的布局也是一樣的啊！
發現到這里，其實我們就找到了重疊子問題了，其實也就是發現可以通過dp[1] 和 dp[2] 來推導出來dp[3]的某種方式。
思考到這里，這道題目就有眉目了。
dp[3]，就是 元素1為頭結點搜索樹的數量 + 元素2為頭結點搜索樹的數量 + 元素3為頭結點搜索樹的數量
元素1為頭結點搜索樹的數量 = 右子樹有2個元素的搜索樹數量 * 左子樹有0個元素的搜索樹數量
元素2為頭結點搜索樹的數量 = 右子樹有1個元素的搜索樹數量 * 左子樹有1個元素的搜索樹數量
元素3為頭結點搜索樹的數量 = 右子樹有0個元素的搜索樹數量 * 左子樹有2個元素的搜索樹數量
有2個元素的搜索樹數量就是dp[2]。
有1個元素的搜索樹數量就是dp[1]。
有0個元素的搜索樹數量就是dp[0]。
所以dp[3] = dp[2] * dp[0] + dp[1] * dp[1] + dp[0] * dp[2]
代碼實現：

class Solution {public int numTrees(int n) {//初始化 dp 數組int[] dp = new int[n + 1];//初始化0個節點和1個節點的情況dp[0] = 1;dp[1] = 1;for (int i = 2; i <= n; i++) {for (int j = 1; j <= i; j++) {//對于第i個節點，需要考慮1作為根節點直到i作為根節點的情況，所以需要累加//一共i個節點，對于根節點j時,左子樹的節點個數為j-1，右子樹的節點個數為i-jdp[i] += dp[j - 1] * dp[i - j];}}return dp[n];}
}