Leetcode 18 java

?????1???????141. 環形鏈表1 題目

?????1???????141. 環形鏈表

給你一個鏈表的頭節點?head?，判斷鏈表中是否有環。

如果鏈表中有某個節點，可以通過連續跟蹤?next?指針再次到達，則鏈表中存在環。為了表示給定鏈表中的環，評測系統內部使用整數?pos?來表示鏈表尾連接到鏈表中的位置（索引從 0 開始）。注意：pos?不作為參數進行傳遞?。僅僅是為了標識鏈表的實際情況。

如果鏈表中存在環?，則返回?true?。否則，返回?false?。

示例 1：

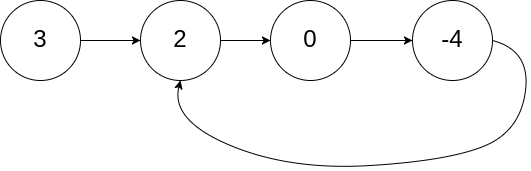
輸入：head = [3,2,0,-4], pos = 1
輸出：true
解釋：鏈表中有一個環，其尾部連接到第二個節點。

示例?2：

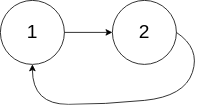
輸入：head = [1,2], pos = 0
輸出：true
解釋：鏈表中有一個環，其尾部連接到第一個節點。

示例 3：

輸入：head = [1], pos = -1
輸出：false
解釋：鏈表中沒有環。

提示：

鏈表中節點的數目范圍是?[0, 104]
-105 <= Node.val <= 105
pos?為?-1?或者鏈表中的一個?有效索引?。

進階：你能用?O(1)（即，常量）內存解決此問題嗎？

2 我的想法

判斷環的思想就是，用一個追蹤指針從頭遍歷到尾指針，存在環的意思是：如果在pos所指示的位置有追蹤指針，那么追蹤指針和尾指針會交匯。

也就是說：

1.如果有環，尾指針指向pos所在節點

2.如果沒有環，第一種情況是單個元素，第二種情況是尾指針一定不指向pos所在節點

/*** Definition for singly-linked list.* class ListNode {*     int val;*     ListNode next;*     ListNode(int x) {*         val = x;*         next = null;*     }* }*/
public class Solution {public boolean hasCycle(ListNode head) {}
}

難道寫一個尾指針.next是否與pos節點一致的判斷就好了嗎？

具體要怎么實現呢，其實鏈表對應節點所在val值要是一樣的呢？我怎么表示pos節點，我這樣的想法可行嗎，如何寫出合適的java代碼？如果是用遍歷的話，空間復雜度是O(1),時間復雜度是O(n)對嗎？寫一個for循環加斷？

3 實現

關于你的想法的分析

你提到 "寫一個尾指針.next 是否與 pos 節點一致的判斷"，這個思路存在幾個問題：

pos 不可用：題目明確說明 pos 是系統內部使用的，不會作為參數傳遞給我們的函數，所以我們無法直接獲取和使用 pos 值
尾指針不存在：在有環的鏈表中，不存在傳統意義上的 "尾指針"（因為鏈表會循環，沒有終點）
val 值可能重復：如你所擔心的，不同節點可能有相同的 val 值，無法通過 val 來判斷是否是同一個節點

所以我們需要一種不依賴 pos、不依賴節點值、且空間效率高的方法。

詳細解題思路

最經典的解法是 "快慢指針法"，也叫 "龜兔賽跑算法"，思路如下：

指針初始化：
- 定義兩個指針，都從鏈表頭部出發
- 慢指針 (slow) 每次只移動 1 步
- 快指針 (fast) 每次移動 2 步
核心邏輯：
- 如果鏈表中沒有環：快指針會先到達鏈表末尾（指向 null）
- 如果鏈表中有環：兩個指針最終一定會在環中相遇
  - 因為快指針比慢指針移動得快，進入環后會逐漸追上慢指針
終止條件：
- 若快指針到達 null，返回 false（無環）
- 若快慢指針相遇，返回 true（有環）

算法為什么有效？

假設鏈表存在環，當慢指針剛進入環時，快指針已經在環內某個位置。此時可以看作快指針在追趕慢指針：

快指針每次比慢指針多走 1 步
相當于慢指針靜止，快指針以每秒 1 步的速度追趕
只要在環內，快指針最終一定會追上慢指針

/*** Definition for singly-linked list.* class ListNode {*     int val;*     ListNode next;*     ListNode(int x) {*         val = x;*         next = null;*     }* }*/
public class Solution {public boolean hasCycle(ListNode head) {// 處理邊界情況：空鏈表一定沒有環if (head == null) {return false;}// 初始化快慢指針ListNode slow = head;      // 慢指針，每次走1步ListNode fast = head.next; // 快指針，每次走2步// 當快慢指針不相等時繼續循環while (slow != fast) {// 快指針到達末尾，說明沒有環// 注意要先判斷fast是否為null，再判斷fast.nextif (fast == null || fast.next == null) {return false;}// 慢指針移動1步slow = slow.next;// 快指針移動2步fast = fast.next.next;}// 循環結束，說明快慢指針相遇，存在環return true;}
}

復雜度分析

時間復雜度：O (n)，其中 n 是鏈表中的節點數
- 無環情況：快指針會遍歷 n/2 個節點就到達末尾
- 有環情況：最壞情況下，兩個指針在環中最多遍歷 n 個節點就會相遇
空間復雜度：O (1)，只使用了兩個指針，不隨鏈表長度變化，滿足題目進階要求

其他可能的解法（但不滿足 O (1) 空間）

哈希表法：
- 遍歷鏈表，將每個節點存入哈希表
- 每次訪問節點前先檢查哈希表，如果已存在則有環
- 空間復雜度 O (n)，不滿足進階要求
標記法：
- 遍歷鏈表時給每個訪問過的節點做標記
- 如果遇到已標記的節點則有環
- 需要修改節點結構，實際中不常用

綜上，快慢指針法是解決這個問題的最優解，既高效又節省空間。

4 兩種解法

先回顧核心問題：為什么判斷鏈表有環不能靠 “節點值” 或 “pos”？

在理解方法前，先明確兩個關鍵前提（也是你之前擔心的點）：

pos 是 “系統內部標記”，我們拿不到：題目里的 pos 只是用來給我們看 “環接在哪”，實際寫代碼時，函數參數只有head，根本沒有 pos 這個值，所以沒法用 “尾指針.next == pos 節點” 這種思路。
節點值可能重復，不能作為判斷依據：比如鏈表是1→2→1→2（有環），兩個 “1” 節點值相同，但卻是不同節點，靠值判斷會誤判；反之，不同節點值也可能組成環，所以 “值” 完全不可靠。

這也是為什么我們需要「哈希表」和「快慢指針」這兩種不依賴 “值” 或 “pos” 的方法 —— 它們判斷的是 “節點本身是否被重復訪問”。

方法一：哈希表法 ——“給走過的節點拍個照，再遇到就是有環”

核心思路：用 “哈希表” 當 “相冊”，記錄所有走過的節點

就像你逛公園時，每經過一個景點就拍張照存手機里。如果逛著逛著，發現眼前的景點 “手機里早就有照片了”，說明你繞回了之前的路（有環）；如果一直走到公園出口（鏈表末尾，head == null），都沒重復照片，說明沒環。

步驟拆解（對應代碼）

我們用 Java 的HashSet（哈希表的一種）來實現 “相冊”，因為HashSet有個特性：添加重復元素時會返回false，這正好幫我們判斷 “是否見過這個節點”。

public class Solution {public boolean hasCycle(ListNode head) {// 1. 初始化哈希表（相冊），存的是“節點本身”，不是節點值！Set<ListNode> seen = new HashSet<ListNode>();// 2. 遍歷鏈表：只要當前節點不為null（沒走到出口），就繼續走while (head != null) {// 3. 嘗試把當前節點加入哈希表：//    - 如果添加失敗（返回false），說明之前見過這個節點→有環，返回true//    - 如果添加成功，說明是第一次見，繼續往下走if (!seen.add(head)) {return true;}// 4. 移動到下一個節點（逛下一個景點）head = head.next;}// 5. 走出循環說明head == null（走到出口），沒環，返回falsereturn false;}
}

關鍵細節：為什么存 “ListNode” 而不是 “val”？

存ListNode（節點對象）：每個節點對象在內存中都有唯一的 “地址”，哈希表判斷重復時，比較的是 “地址”，能確保 “同一個節點才會被判定為重復”。
存val（節點值）：如之前說的，值可能重復，會導致 “不同節點被誤判為重復”，比如1→2→1（無環），第二個 “1” 會被誤判為重復，返回錯誤的true。

復雜度理解

時間復雜度 O (N)：最壞情況是 “鏈表無環”，我們要把所有 N 個節點都遍歷一遍，每個節點的 “添加” 和 “判斷” 操作在哈希表中是 O (1)，所以總時間是 O (N)。
空間復雜度 O (N)：最壞情況是 “鏈表無環”，我們要把 N 個節點都存進哈希表，所以空間是 O (N)—— 這也是它的缺點，不如快慢指針省空間。

方法二：快慢指針法（Floyd 判圈算法）——“讓兔子和烏龜賽跑，追上就是有環”

核心思路：用兩個速度不同的指針，模擬 “兔子（快）” 和 “烏龜（慢）” 在鏈表上跑

如果鏈表沒環：兔子跑得比烏龜快，會先跑到鏈表末尾（fast == null或fast.next == null），永遠追不上烏龜。
如果鏈表有環：兔子會先進入環，然后在環里繞圈；等烏龜也進入環后，兔子因為速度快，總會在某個時刻追上烏龜（兩個指針指向同一個節點）。

步驟拆解（對應代碼）

先明確指針規則：

慢指針（烏龜）：每次走 1 步（slow = slow.next）
快指針（兔子）：每次走 2 步（fast = fast.next.next）

public class Solution {public boolean hasCycle(ListNode head) {// 1. 處理邊界：空鏈表（head==null）或只有1個節點（head.next==null），肯定沒環if (head == null || head.next == null) {return false;}// 2. 初始化指針：慢指針從head出發，快指針從head.next出發（關鍵細節，后面解釋）ListNode slow = head;ListNode fast = head.next;// 3. 循環：只要快慢指針沒相遇，就繼續跑while (slow != fast) {// 4. 檢查快指針是否到末尾：如果fast或fast.next是null，說明沒環if (fast == null || fast.next == null) {return false;}// 5. 烏龜走1步，兔子走2步slow = slow.next;fast = fast.next.next;}// 6. 跳出循環→快慢指針相遇，說明有環，返回truereturn true;}
}

關鍵細節 1：為什么初始時快指針要從`head.next`出發，而不是和慢指針一起從`head`出發？

這是為了適配while循環的 “先判斷，后執行” 邏輯：

如果兩個指針都從head出發：初始時slow == fast，while (slow != fast)的條件直接不滿足，循環不執行，直接返回false—— 但此時如果鏈表有環（比如head自己指向自己），就會誤判。
快指針從head.next出發：初始時slow = head，fast = head.next，slow != fast，循環能正常開始；即使鏈表是head自環（head.next = head），第一次循環時：
- slow會走到head.next = head
- fast會走到head.next.next = head.next = head
- 此時slow == fast，跳出循環返回true，判斷正確。

如果想用 “兩個指針都從head出發”，可以把while改成do-while（先執行，后判斷），代碼如下（邏輯完全等價，只是循環方式不同）：

public boolean hasCycle(ListNode head) {if (head == null) return false;ListNode slow = head, fast = head;// do-while：先移動，再判斷是否相遇do {// 快指針到末尾，沒環if (fast == null || fast.next == null) return false;slow = slow.next;fast = fast.next.next;} while (slow != fast);// 相遇，有環return true;
}

關鍵細節 2：為什么快指針走 2 步，不是 3 步、4 步？

核心是 “快指針速度比慢指針快”，走 2 步是最簡潔的選擇：

走 2 步時，每次循環快慢指針的距離會減少 1（比如初始距離 1，下次距離 0；初始距離 2，下次距離 1，再下次距離 0），必然會相遇。
走 3 步、4 步也能實現，但代碼會更復雜（比如要多判斷fast.next.next是否為 null），且沒有性能優勢，所以 2 步是最優選擇。

復雜度理解

時間復雜度 O (N)：
- 無環情況：快指針走 N/2 步就到末尾（因為每次走 2 步），時間 O (N)。
- 有環情況：最壞是 “環很小，烏龜進環前要走很多步”，但總體來看，快指針最多繞環 1 圈就能追上烏龜，總步數還是 O (N)。
空間復雜度 O (1)：只用到slow和fast兩個指針，不管鏈表多長，都只占 2 個指針的空間，完全符合題目 “O (1) 內存” 的進階要求。

兩種方法的對比：怎么選？

對比維度	哈希表法	快慢指針法
核心邏輯	記錄已訪問節點，看是否重復	速度差導致相遇
時間復雜度	O(N)	O(N)
空間復雜度	O (N)（需要存節點）	O (1)（只需要兩個指針）
代碼簡潔度	較簡潔（依賴哈希表 API）	稍復雜（需處理指針初始化）
適用場景	除了判斷環，還想記錄節點	只需要判斷環，追求省空間

實際面試中，快慢指針法是更優的選擇—— 因為它滿足 O (1) 空間，也是面試官更想考察的思路（能體現對鏈表特性的深入理解）；哈希表法更偏向 “直觀思路”，適合作為輔助理解的方法。

通過這兩個方法的拆解，你應該能徹底明白 “判斷鏈表有環” 的核心邏輯了～下次遇到類似問題，不管是用哈希表還是快慢指針，都能清晰地寫出代碼啦！

【解釋：if (!seen.add(head))】

我們來詳細解釋一下你看不懂的這行代碼：if (!seen.add(head))

這句話的作用

這句話的意思是：嘗試把當前節點head添加到哈希表seen中，如果添加失敗（說明這個節點已經在哈希表中存在了），就返回true（表示有環）

逐步拆解

seen是一個HashSet<ListNode>類型的集合，用來存儲我們已經訪問過的節點
seen.add(head)這個方法的特性：
- 當我們往 HashSet 中添加元素時，如果這個元素之前不存在，就會添加成功，返回true
- 如果這個元素之前已經存在，就會添加失敗，返回false
!是邏輯非運算符，用來取反：
- 如果seen.add(head)返回true（添加成功，是新節點），那么!true就是false，不會進入 if 語句
- 如果seen.add(head)返回false（添加失敗，節點已存在），那么!false就是true，會進入 if 語句，執行return true